1519. Formula 1
Memory limit: 64 MB
Background
Problem
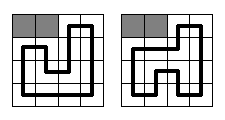
Input
Output
Samples
| input | output |
|---|---|
4 4 **.. .... .... .... |
2 |
4 4 .... .... .... .... |
6 |
Problem Source: Timus Top Coders: Third Challenge
My submissions All submissions (10084) All accepted submissions (3166) Solutions rating (868)
题意:给出n*m的棋盘,有一些格子有障碍,求有多少个不经过障碍的哈密顿回路。

时合法的状态数总数为1333113个,可以解决本题。
4.可以发现轮廓线以上的路径一定互不相交,并且两两匹配,所以可以用括号序列来表示状态,0表示左括号"(",1表示右括号”)",括号的意义即使到轮廓线上的路径是出路径还是入路径。
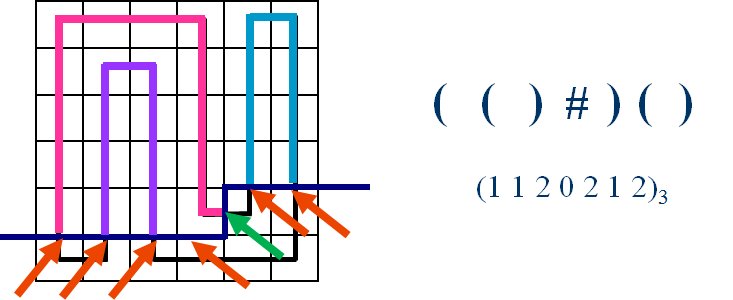
可以发现,一行有m个格子,但是却有m+1个状态,因为在转移的时候我们要考虑到,当前处理的格子的右边的情况(绿色箭头)
每一次转移之后相当于是轮廓线上当前决策格子的左插头改成下插头,上插头改成右插头的状态。
每一次转移之后改变的是对应格子轮廓线上连通的状态,我们只关心当前格子轮廓线以上的连线终止与轮廓线上(由于要形成哈密顿回路,所以不存在自环)的情况,而并不在意轮廓线之下的连线方式。
那么分情况考虑转移(把橘色的称为左插头,绿色的称为上插头)

(1)上,左插头都没有,而且当前格子(x,y),(x+1,y),(x,y+1)均不为障碍,则可以新建一个连通块。
...00... --------> ...12...
(2)仅有有上插头,或仅有下插头,延续原来的连通分量即可。
...10... --------> ...12...
(3)上下插头都有。
3.1,上下插头均为出路径,画图可知即使两个连通分量左边合并,需要找到相应状态最左边那个右括号将其修改为左括号。
...11...2...2... -------> ...00...1...2
3.2,左插头为入路径,上插头为出路径,即直接将对应状态位置上的左右括号消去即可。
...12... ------> ...00...
3.3,做插头为出路径,右插头为入路径,这个情况下就是答案的状态了,而且只能出现在最右下角的那个格子(其余的不合法)。
细节
注意题目的空间,以及还可以加上的优化。
我们把每一次的状态hash起来(而不是动态存储)
一种数据 :
1
.
三进制存储?为了方便,我们采用4进制(位运算中两位来表示一位)
CODE:
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<vector> 5 #include<cstdlib> 6 #include<cmath> 7 #include<cstring> 8 using namespace std; 9 #define yyj(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout); 10 #define CC(a,b) memset(a,b,sizeof(a)); 11 #define u64 unsigned long long 12 #define llg long long 13 const int sz=199917; 14 llg n,m,state[2][sz],tail,hash[sz],bit[20],tot[2],nn,mm,k=0; 15 u64 dp[2][sz],ans; 16 17 char mp[100][100]; 18 19 llg init() 20 { 21 llg cs=0; 22 CC(mp,0); 23 CC(dp,0); 24 tot[0]=dp[0][1]=1; 25 state[0][1]=0; 26 ans=k=0; char ch; 27 for (llg i=1;i<=n;i++) 28 { 29 scanf("%c",&ch); 30 for (llg j=1;j<=m;j++) 31 { 32 scanf("%c",&ch); 33 mp[i][j]=ch=='.'; 34 if (ch=='.') cs++; 35 if (mp[i][j]) nn=i,mm=j; 36 } 37 } 38 return cs; 39 } 40 41 void in(llg s,u64 sum) 42 { 43 llg p=s%sz; 44 while (hash[p]) 45 { 46 if (state[k][hash[p]]==s) 47 { 48 dp[k][hash[p]]+=sum; 49 return ; 50 } 51 p++; 52 if (p==sz) p=0; 53 } 54 hash[p]=++tot[k]; 55 state[k][hash[p]]=s; 56 dp[k][hash[p]]=sum; 57 } 58 59 void work() 60 { 61 for (llg i=1;i<=n;i++) 62 { 63 for (llg j=1;j<=m;j++) 64 { 65 k^=1; 66 CC(hash,0); 67 tot[k]=0; 68 for (llg u=1;u<=tot[1-k];u++) 69 { 70 llg s=state[1-k][u],p=(s>>bit[j-1])&3,q=(s>>bit[j])&3; 71 u64 sum=dp[1-k][u]; 72 if (!mp[i][j]) 73 { 74 if (!q && !p) in(s,sum); 75 } 76 else 77 { 78 if (!p && !q) 79 { 80 if (!mp[i][j+1] || !mp[i+1][j]) continue; 81 s=s^(1<<bit[j-1])^(1<<bit[j]<<1); 82 in(s,sum); 83 } 84 else 85 if (!p && q) 86 { 87 if (mp[i][j+1]) in(s,sum); 88 if (mp[i+1][j]) s=s^q*(1<<bit[j-1])^q*(1<<bit[j]),in(s,sum); 89 } 90 else 91 if (p && !q) 92 { 93 if (mp[i+1][j]) in(s,sum); 94 if (mp[i][j+1]) s=s^p*(1<<bit[j-1])^p*(1<<bit[j]),in(s,sum); 95 } 96 else 97 if (p+q==2) 98 { 99 llg nd=1; 100 for (llg u=j+1;j<=m;u++) 101 { 102 llg w=(s>>bit[u])&3; 103 if (w==1) nd++; 104 if (w==2) nd--; 105 if (!nd) {s-=(1<<bit[u]); break;} 106 } 107 s=s^(1<<bit[j])^(1<<bit[j-1]),in(s,sum); 108 } 109 else 110 if (p+q==4) 111 { 112 llg nd=1; 113 for (llg u=j-2;u>=1;--u) 114 { 115 llg w=(s>>bit[u])&3; 116 if (w==2) nd++; 117 if (w==1) nd--; 118 if (!nd) {s+=(1<<bit[u]); break;} 119 } 120 s=s^(1<<bit[j]<<1)^(1<<bit[j-1]<<1); 121 in(s,sum); 122 } 123 else 124 if (p==1 && q==2) 125 { 126 if (i==nn && j==mm) ans+=sum; 127 } 128 else 129 if (p==2 && q==1) 130 { 131 s=s^(1<<bit[j-1]<<1)^(1<<bit[j]); 132 in(s,sum); 133 } 134 135 } 136 } 137 } 138 for (llg j=1;j<=tot[k];j++) state[k][j]<<=2; 139 } 140 cout<<ans<<endl; 141 } 142 143 int main() 144 { 145 //yyj("a"); 146 for (llg i=0;i<=13;i++) bit[i]=(i<<1); 147 while (scanf("%lld%lld",&n,&m)!=EOF) 148 { 149 if (init()%2) {cout<<"0"<<endl; continue;} 150 work(); 151 } 152 return 0; 153 }
参考:《基于连通性状态压缩的动态规划问题_Cdq》》--陈丹琦
博客:http://www.cnblogs.com/Tunix/p/4312203.html