1.问题
给定n个大小不等的圆c1,c2,…,cn,现要将这n个圆排进一个矩形框中,且要求各圆与矩形框的底边相切。圆排列问题要求从n个圆的所有排列中找出有最小长度的圆排列。例如,当n=3,且所给的3个圆的半径分别为1,1,2时,这3个圆的最小长度的圆排列如图所示。其最小长度为。
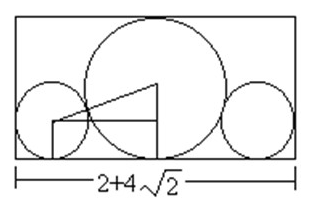
2. 解析
圆排列问题的解空间是一棵排列树,按照回溯法搜索排列数的算法框架
设所有圆的半径为 A = [r1 , r2 , r3 … , rn];
那么对应的排列数有 A[1 : n ]的全排列构成
那么我们通过回溯法计算最优圆排列的时候需要注意几个问题
(1)首先是相切问题:
如图:
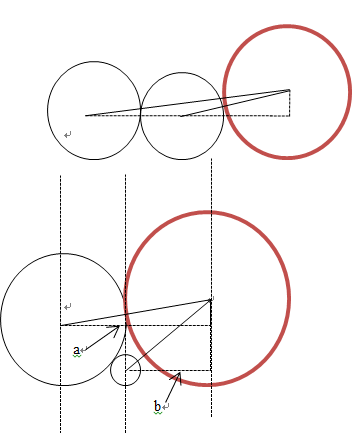
在思考本题是很容易先入为主的认为,相邻的圆是相切的,但是实际上通过这个图我们可以知道,最后一个圆是有可能和它之前的任意一个圆相切的,如果以相邻圆相切的思路做题,得出的结果有可能会偏小
(2)其次是剪枝问题:
在圆排列问题中我们需要构造全排列,通过排列组合可以知道构造全排列的时间复杂度为O(n!),但是实际上有一些圆排列在仅有一部份圆的时候其长度就已经超过了最小长度,因此有这些部分圆排列所演变出的圆排列明显是不符合的。
这可以在某些情况下减少算法的时间复杂度。
3.设计
计算当前圆的横坐标
1 double get_center(int t) 2 { 3 double tmp = 0; 4 for (int i = 1; i < t; ++i) 5 { 6 double val = x[i] + 2.0 * sqrt(r[t] * r[i]); //. 目标圆T有可能能够和排在它之前的任意一个圆相切,因此需要以一判断取最大值 7 tmp = max(tmp, val); 8 } 9 return tmp; 10 }
通过回溯法够成圆排列的全排列,因为用于记录圆横坐标的x数组,定义为了全局变量,因此第一个圆的横坐标被默认设置为了0,在计算圆排列长度进行剪枝的时候需要加上第一个圆的半径。
1 void dfs(int pos) 2 { 3 if (pos == n + 1) 4 { 5 get_ans(); 6 } 7 else 8 { 9 for (int i = pos; i <= n; ++i) 10 { 11 swap(r[pos], r[i]);//构造全排列 12 double X_pos = get_center(pos);//获取当前 13 if (X_pos + r[pos] + r[1] < minlen) //进行一定程度上的减枝 14 { 15 x[pos] = X_pos; 16 dfs(pos + 1); 17 } 18 swap(r[pos], r[i]); //构造全排列 19 } 20 } 21 }
4.分析
由排列组合可知,生成一个长度为n的序列的全排列的时间复杂度为O(n!)
同时在这个算法中,对于每一个排列中的每一个圆,它有可能和在它之前的任意一个圆相切,为了正确的确定是与那个圆相切需要使用for循环进行遍历,通过遍历找到与之相切的圆,其每次的时间复杂度为O(n)
综上所述,计算最小圆排列的复杂度为O(n * n!)
5.源码

1 #include<iostream> 2 #include<cmath> 3 #include<algorithm> 4 using namespace std; 5 6 7 const int maxn = 1e5 + 10; 8 double minlen = 1e5; 9 double x[maxn], r[maxn]; 10 // x存储每个圆心的横坐标 , r存储每个圆的半径 , 11 // 由于x数组为全局变量,因此初始化为0,因此第一个圆的横坐标默认为0,因此在计算最小圆排列长度的时候还需要注意加上第一个圆的半径 12 double bestR[maxn]; // 存储最优的圆排列的半径顺序 13 int n; 14 15 double get_center(int t) 16 { 17 double tmp = 0; 18 for (int i = 1; i < t; ++i) 19 { 20 double val = x[i] + 2.0 * sqrt(r[t] * r[i]); //. 目标圆T有可能能够和排在它之前的任意一个圆相切,因此需要以一判断取最大值 21 tmp = max(tmp, val); 22 } 23 return tmp; 24 } 25 26 void get_ans() 27 { 28 double minn = 0, maxx = 0; // 计算最优圆排列的最左端 和 最右端 29 for (int i = 1; i <= n ; ++i) 30 { 31 if (x[i] - r[i] < minn) minn = x[i] - r[i]; 32 if (x[i] + r[i] > maxx) maxx = x[i] + r[i]; 33 } 34 if (maxx - minn < minlen) 35 { 36 minlen = maxx - minn; // 更新最小圆排列 37 for (int i = 1; i <= n ; ++i) 38 { 39 bestR[i] = r[i]; 40 } 41 } 42 } 43 44 45 void dfs(int pos) 46 { 47 if (pos == n + 1) 48 { 49 get_ans(); 50 } 51 else 52 { 53 for (int i = pos; i <= n; ++i) 54 { 55 swap(r[pos], r[i]);//构造全排列 56 double X_pos = get_center(pos);//获取当前 57 if (X_pos + r[pos] + r[1] < minlen) //进行一定程度上的减枝 58 { 59 x[pos] = X_pos; 60 dfs(pos + 1); 61 } 62 swap(r[pos], r[i]); //构造全排列 63 } 64 } 65 } 66 67 68 int main() 69 { 70 cout << "输入圆的个数:" << endl; 71 cin >> n; 72 cout << "依次输入圆的半径" << endl; 73 for (int i = 1; i <= n; ++i) 74 { 75 cin >> r[i]; 76 } 77 for (int i = 1; i <= n; ++i) 78 { 79 cout << "第" << i << "个圆的半径为:" << r[i] << endl; 80 } 81 dfs(1); 82 cout << "最小圆排列的长度为:" << minlen << endl; 83 cout << "最优原排列的顺序对应的半径分别为:"; 84 for (int i = 1; i <= n; ++i) 85 { 86 cout << bestR[i] << " "; 87 } 88 cout << endl; 89 return 0; 90 }
https://github.com/BambooCertain/Algorithm.git
