
【题解】
原来线段树还可以这么玩。。
我们用线段树维护连通性。对于一个矩形,我们用4个标记维护4个点的联通情况,再用两个标记维护右边两个点与它们右边的与它们在同一行的点的联通情况。
画图表示,就是
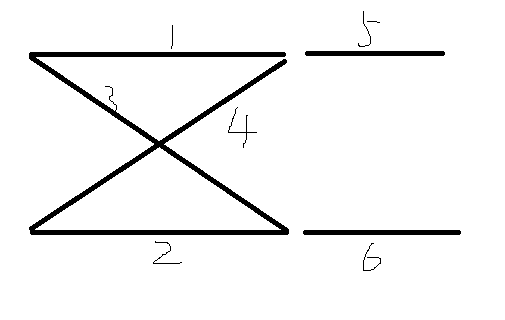
另一个关键问题是对于询问(r1,c1,r2,c2),并不是只可以走c1到c2之间的部分,它可以绕路走,这就需要我们在处理询问的时候把c1,c2进行扩展。具体说来,就是让c1一直向左走,让c2一直向右走,
然后查询新的(r1,c1,r2,c2). 为什么这样做是对的呢?
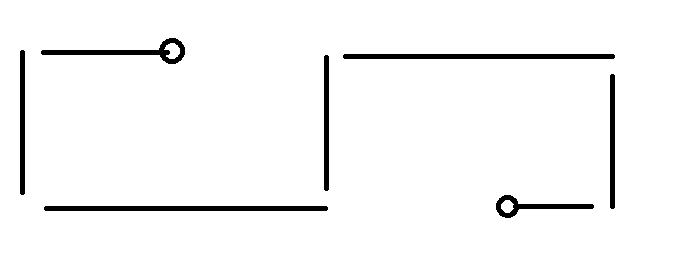

通过上图我们可以发现要绕路走必须走到跟r1,r2不同的行,也就是一定会通过c1左边的竖着的边以及c2右边的竖着的边。而且一定存在一种走法使得绕路走的部分形成一个类似括号的形状。我们把c1一直左移得到c1',就可以保证[c1',c1]之间一定有竖着的边(如果c1到c1左边联通的部分之间有竖边存在的话)。右边的c2也是同理。这样查询新的c1,c2就转化成了没有绕路走的情况。

1 // luogu-judger-enable-o2 2 #include<cstdio> 3 #include<algorithm> 4 #define N 100010 5 #define rg register 6 #define ls (u<<1) 7 #define rs (u<<1|1) 8 using namespace std; 9 int n; 10 struct tree{ 11 int t1,t2,t3,t4,t5,t6; 12 }a[N<<2]; 13 inline int read(){ 14 int k=0,f=1; char c=getchar(); 15 while(c<'0'||c>'9')c=='-'&&(f=-1),c=getchar(); 16 while('0'<=c&&c<='9')k=k*10+c-'0',c=getchar(); 17 return k*f; 18 } 19 inline void pushup(int u){ 20 a[u].t1=(a[ls].t1&&a[ls].t5&&a[rs].t1)||(a[ls].t3&&a[ls].t6&&a[rs].t4); 21 a[u].t2=(a[ls].t2&&a[ls].t6&&a[rs].t2)||(a[ls].t4&&a[ls].t5&&a[rs].t3); 22 a[u].t3=(a[ls].t1&&a[ls].t5&&a[rs].t3)||(a[ls].t3&&a[ls].t6&&a[rs].t2); 23 a[u].t4=(a[ls].t4&&a[ls].t5&&a[rs].t1)||(a[ls].t2&&a[ls].t6&&a[rs].t4); 24 a[u].t5=a[rs].t5; 25 a[u].t6=a[rs].t6; 26 } 27 void build(int u,int l,int r){ 28 if(l<r){ 29 int mid=(l+r)>>1; 30 build(ls,l,mid); build(rs,mid+1,r); 31 } 32 else a[u].t1=a[u].t2=1; 33 } 34 void update(int u,int l,int r,int pos,int type,int del){ 35 if(l==r){ 36 if(type==3||type==4) a[u].t3=a[u].t4=del; 37 if(type==5) a[u].t5=del; 38 if(type==6) a[u].t6=del; 39 return; 40 } 41 int mid=(l+r)>>1; 42 if(pos<=mid) update(ls,l,mid,pos,type,del); 43 else update(rs,mid+1,r,pos,type,del); 44 pushup(u); 45 } 46 tree query(int u,int l,int r,int ql,int qr){ 47 if(ql<=l&&r<=qr) return a[u]; 48 tree ret,L,R; int mid=(l+r)>>1; 49 L=R=(tree){1,1,1,1,1,1}; 50 if(ql<=mid) ret=L=query(ls,l,mid,ql,qr); 51 if(qr>mid) ret=R=query(rs,mid+1,r,ql,qr); 52 if(ql<=mid&&qr>mid){ 53 ret.t1=(L.t1&&L.t5&&R.t1)||(L.t3&&L.t6&&R.t4); 54 ret.t2=(L.t2&&L.t6&&R.t2)||(L.t4&&L.t5&&R.t3); 55 ret.t3=(L.t1&&L.t5&&R.t3)||(L.t3&&L.t6&&R.t2); 56 ret.t4=(L.t4&&L.t5&&R.t1)||(L.t2&&L.t6&&R.t4); 57 } 58 return ret; 59 } 60 int goleft(int u,int l,int r,int type,int pos){ 61 if(r==pos&&((type==1&&a[u].t1)||(type==2&&a[u].t2))) return l; 62 int mid=(l+r)>>1; 63 if(pos<=mid) return goleft(ls,l,mid,type,pos); 64 int L=goleft(rs,mid+1,r,type,pos); 65 if(L==mid+1&&((type==1&&a[ls].t5)||(type==2&&a[ls].t6))) 66 return goleft(ls,l,mid,type,mid); 67 return L; 68 } 69 int goright(int u,int l,int r,int type,int pos){ 70 if(l==pos&&((type==1&&a[u].t1)||(type==2&&a[u].t2))) return r; 71 int mid=(l+r)>>1; 72 if(pos>mid) return goright(rs,mid+1,r,type,pos); 73 int R=goright(ls,l,mid,type,pos); 74 if(R==mid&&((type==1&&a[ls].t5)||(type==2&&a[ls].t6))) 75 return goright(rs,mid+1,r,type,mid+1); 76 return R; 77 } 78 int main(){ 79 n=read(); build(1,1,n); 80 while(1){ 81 char s[10]; scanf("%s",s+1); 82 while(s[1]!='E'&&s[1]!='C'&&s[1]!='O'&&s[1]!='A') scanf("%s",s+1); 83 if(s[1]=='E') break; 84 int r1=read(),c1=read(),r2=read(),c2=read(); 85 if(c1>c2) swap(c1,c2),swap(r1,r2); 86 if(s[1]=='C'){ 87 if(c1==c2) update(1,1,n,c1,3,0); 88 if(r1==r2) update(1,1,n,c1,r1==1?5:6,0); 89 } 90 if(s[1]=='O'){ 91 if(c1==c2) update(1,1,n,c1,3,1); 92 if(r1==r2) update(1,1,n,c1,r1==1?5:6,1); 93 } 94 if(s[1]=='A'){ 95 c1=goleft(1,1,n,r1,c1); c2=goright(1,1,n,r2,c2); 96 tree ans=query(1,1,n,c1,c2); 97 bool flag=0; 98 if(r1==1&&r2==1) flag=ans.t1; 99 if(r1==2&&r2==2) flag=ans.t2; 100 if(r1==1&&r2==2) flag=ans.t3; 101 if(r1==2&&r2==1) flag=ans.t4; 102 puts(flag?"Y":"N"); 103 } 104 } 105 return 0; 106 }
