自己想出来了!这个dp比较简单,而且转移也很简单,很自然,直接上代码就行了.
题干:
一种EDIT字母编辑器,它的功能是可以通过不同的变换操作可以把一个源串X [l..m]变换为新的目标串y[1..n]。EDIT提供的变换操作有:
源串中的单个字符可被删除(delete);
被替换 (replace);
被复制到目标串中去(copy);
字符也可被插入(insert);
源串中的两个相邻字符可进行交换并复制到目标串中去(twiddle);
在完成其它所有操作之后,源串中余下的全部后缀就可用删至行末的操作删除(kill)。
例如,将源"algorithm"转换成目标串"altruistic"的一种方法是采取下面的操作序列:
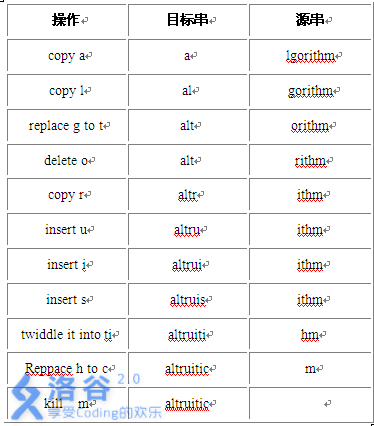
要达到这个结果还可能有其它一些操作序列。
操作delete,replace,copy,insert,twiddle和kill中每一个都有一个相联系的代价cost。例如
cost(delete)=3;
cost(replace)=6;
cost(copy)=5;
cost(insert)=4;
cost(twiddle)=4;
cost(kill)=被删除的串长*cost(delete)-1;一个给定的操作序列的代价为序列中各操作代价之和。 例如上述操作序列的代价为
3*cost(copy)+2*cost(replace)+cost(delete)+3*cost(insert) + cost(twiddle) +cost(kill)
=3*5+2*6+3+3*4+4+1*3-1=48
编程任务:
给定两个序列x[1..m],y[1..n]和一些操作代价集合,X到Y的最短距离为将X转化为Y的最小的转换序列的代价。请给出一个算法来找出x[1..m]至y[1..n]的最短距离。
输入输出格式
输入格式:
第一行:源序列x[1..m]。(m<200)
第二行:目标序列y[1..n]。(n<200)
第三行:5个正整数(<100):分别是:delete 、replace 、copy、 insert、 twiddle的代价。
输出格式:
X到Y的最短距离(最小代价和)。
输入输出样例
algorithm altruistic 3 6 5 4 4
48
代码:
#include<iostream> #include<cstdio> #include<cmath> #include<ctime> #include<queue> #include<algorithm> #include<cstring> using namespace std; #define duke(i,a,n) for(int i = a;i <= n;i++) #define lv(i,a,n) for(int i = a;i >= n;i--) #define clean(a) memset(a,0,sizeof(a)) const int INF = 1 << 30; typedef long long ll; typedef double db; template <class T> void read(T &x) { char c; bool op = 0; while(c = getchar(), c < '0' || c > '9') if(c == '-') op = 1; x = c - '0'; while(c = getchar(), c >= '0' && c <= '9') x = x * 10 + c - '0'; if(op) x = -x; } template <class T> void write(T x) { if(x < 0) putchar('-'), x = -x; if(x >= 10) write(x / 10); putchar('0' + x % 10); } int n,m; char x[205],y[205]; int del,rep,cop,ins,twi; int f[205][205]; int main() { scanf("%s",x + 1); scanf("%s",y + 1); n = strlen(x + 1); m = strlen(y + 1); read(del);read(rep);read(cop); read(ins);read(twi); memset(f,127,sizeof(f)); f[0][0] = 0; duke(i,1,m) f[i][0] = i * ins; duke(i,1,n) f[0][i] = i * del; duke(i,1,m) { duke(j,1,n) { f[i][j] = min(f[i][j],f[i - 1][j] + ins); f[i][j] = min(f[i][j],f[i - 1][j - 1] + rep); if(y[i] == x[j]) f[i][j] = min(f[i][j],f[i - 1][j - 1] + cop); if(i > 1 && j > 1 && y[i - 1] == x[j] && y[i] == x[j - 1]) f[i][j] = min(f[i][j],f[i - 2][j - 2] + twi); f[i][j] = min(f[i][j],f[i][j - 1] + del); } } int minn = INF; duke(i,1,n - 1) minn = min(minn,f[m][i] + (n - i) * del - 1); minn = min(minn,f[m][n]); printf("%d ",minn); return 0; } /* algorithm altruistic 3 6 5 4 4 */