第三节、矩阵乘法

我们之前已经接触了一些矩阵乘法的规则，现在来系统地学习一下。

一、基本要求

并不是随便拿两个矩阵就可以作矩阵乘法，想要做矩阵乘法，必须满足以下要求：

第一个矩阵的列数等于第二个矩阵的行数。

即如果第一个矩阵是m×n的，那么第二个必须是n×p的，其中m、n、p为任意正整数（a行b列可以用a×b表示）

二、基本性质

1. 满足结合律 A(BC)=(AB)C
2. 满足交换律 A(B+C)=AB+AC 、 (A+B)C=AC+BC
3. 满足对数乘的结合性 k(AB)=(kA)B=A(kB)  ，k为任意常数
4. 一般不满足交换律AB≠BA

三、矩阵乘法运算

　　以下叙述中，默认以AB=C表示，其中A为m×n矩阵，B为n×P矩阵，C为二矩的阵乘积（m×p矩阵）。

　　另，默认用A_ij表示A矩阵第i行第j列元素

　1.基本方法（按行与列点乘考虑）

　　用A中的每一行与B中的每一列进行点乘，并将得到的结果写在C相应的位置（用的A中的哪行就写在C的哪行，用的B的哪列就写在C的由A确定的行的哪列）

　　

　　即（下图源自百度百科）

　　

　2.按列考虑

　　前面说过，在一个矩阵右边乘上一个矩阵相当于对该矩阵作列变换，在矩阵右边乘一个列向量相当于对该矩阵的列进行线性组合。

　　沿袭楼上传统，我们假设A=，B=，顺便写上已经求出来的C=

　　其中A乘以B的第一列等于

　　A乘以B的第二列等于

　　我们的结果是A乘以B的第一列等于C的第一列，A乘以B的第二列等于C的第二列。

　　即，我们可以把B考虑成摆放在一起的p个单独的列向量，作乘法时用A乘以每一个列向量，从而可以得到p个列，将他们摆放在一起就得到了整个矩阵相乘的结果。

　　也就是C中的列是A各列的线性组合，而B决定线性组合的方式

　　用另一种说法：矩阵乘以矩阵就是矩阵乘以列向量的叠加，也就是B对A的列进行线性组合的叠加（也许用“叠加”不是很恰当，也许可以用“拼凑”？“组合”？“拼合”？能理解这个意思就好）

　3.按行考虑

　　既然可以按列考虑，自然也可以按行考虑。

　　前面也介绍过，在一个矩阵左边乘上一个矩阵相当于对该矩阵作行变换，在矩阵左边乘一个行向量相当于对该矩阵的行进行线性组合。

　　接着沿袭楼上传统，我们假设A=，B=，还有他们的乘积C=

　　A的第一行乘以B等于 1[1  4] + 2[2  5] + 3[3  6] = [ 14  32 ]

　　A的第二行乘以B等于 4[1  4] + 5[2  5] + 6[3  6] = [ 32  77 ]

　　我们可以把A考虑成摆放在一起的m个单独的行向量，作乘法时用A的每一行乘以B，从而可以得到m个行，将他们摆放在一起就得到了整个矩阵相乘的结果。

　　即，C中的行是B各行的线性组合，而组合的方式由A决定

　　我想，如果你理解了列的关系，那么行的关系也可以很容易地理解。

　　如果你对按行考虑和按列考虑的思想感到很茫然，或者根本没听说过这种思考方式，那一定是你没看或没仔细看前面的两节内容，请回头仔细阅读。

　4.按列乘以行考虑

　　基本方法用行点乘列得到一个数，而用列与行考虑得到的则是一个矩阵（m×p）

　　还以A=，B=，C=为例。

　　用A的第一列乘上B的第一行，得到

　　用A的第二列乘上B的第二行，得到

　　用A的第二列乘上B的第二行，得到

　　将三个矩阵相加，我们得到了矩阵C。

　　也就是说，矩阵相乘的结果等于A矩阵的各列与B矩阵对应的行的乘积的和。

　5.特殊性质：分块相乘

 　　分块相乘的意思就是你可以将矩阵分成匹配的多块（匹配即满足矩阵乘法规则），然后将每一块看成一个数进行乘法，规则与正常矩阵乘法相同，只是运算的元素由数字变成了更小的矩阵。

　　举个例子，A=，B=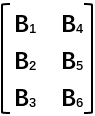，其中，A与B中各元素都是矩阵。

　　则C=。

　　（注：计算机在矩阵较大时使用分块乘法可提高效率）