A:Careful Thief
题意:给出n个区间,每个区间的每个位置的权值都是v,然后找长度为k的区间,使得这个区间的所有位置的权值加起来最大,输出最大权值, 所有区间不重叠
思路:贪心的想法,长度为k的区间的起始点肯定是某个区间的起始点,或者长度为k的区间的结束点肯定是某个区间的结束点。
因为存在最优的答案,它的起点不在某个区间的起点,那么只有两种情况。
1° 不属于任何已知区间
2° 在某个已知区间的内部
首先考虑第一种情况 如果不属于任何已知区间,那么根据贪心,我肯定能够往右移使得它是某个区间起点,这样得到的新的答案肯定大于等于原来的答案,因为我移动的这段区间的权值都为0
那么第二种情况,假如现在涵盖的区间横跨两个区间,那么我肯定能够右移结束点使得它与最后的那个区间的结束点对齐,或者左移起始点使得它跟最左边涵盖到的区间的起始点对齐,使得答案更大
然后双指针搞一搞

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define ll long long 6 7 #define N 100010 8 9 int t, m, k; 10 11 struct node 12 { 13 int l, r; 14 ll v; 15 ll sum; 16 inline node() {} 17 inline node(int l, int r, int v) : l(l), r(r), v(v) {} 18 19 inline void scan() 20 { 21 scanf("%d%d%lld", &l, &r, &v); 22 sum = (ll)(r - l + 1) * v; 23 } 24 25 inline bool operator < (const node& b) const 26 { 27 return l < b.l; 28 } 29 }arr[N]; 30 31 int main() 32 { 33 scanf("%d", &t); 34 while (t--) 35 { 36 scanf("%d%d", &m, &k); 37 for (int i = 1; i <= m; ++i) 38 arr[i].scan(); 39 40 sort(arr + 1, arr + m + 1); 41 int L, R; 42 int j = 1; 43 ll ans = 0; 44 ll tmp = 0; 45 for (int i = 1; i <= m; ++i) 46 { 47 L = arr[i].l; 48 R = L + k - 1; 49 while (arr[j].r <= R && j <= m) 50 { 51 tmp += arr[j].sum; 52 ++j; 53 } 54 ll res = 0; 55 if(j <= m) 56 { 57 res = arr[j].v * max(0, R - arr[j].l + 1); 58 } 59 tmp += res; 60 ans = max(ans, tmp); 61 tmp -= res; 62 tmp -= arr[i].sum; 63 } 64 tmp = 0; 65 j = m; 66 for(int i = m; i >= 1; --i) 67 { 68 R = arr[i].r; 69 L = R - k + 1; 70 while(arr[j].l >= L && j >= 1) 71 { 72 tmp += arr[j].sum; 73 --j; 74 } 75 ll res = 0; 76 if(j >= 1) 77 { 78 res = arr[j].v * max(0, arr[j].r - L + 1); 79 } 80 tmp += res; 81 ans = max(ans, tmp); 82 tmp -= res; 83 tmp -= arr[i].sum; 84 } 85 printf("%lld ",ans); 86 } 87 return 0; 88 }
B:Friends and Cookies
水。

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define ll long long 6 7 #define N 1010 8 9 int t, n; 10 11 ll x; 12 13 ll ans[N]; 14 15 int main() 16 { 17 scanf("%d", &t); 18 while (t--) 19 { 20 scanf("%lld%d", &x, &n); 21 if (n == 1) 22 { 23 printf("%lld ", x); 24 continue; 25 } 26 ll len = n + n - 2; 27 ll base = x / len; 28 ll MOD = x % len; 29 for (int i = 1; i <= n; ++i) 30 { 31 if (i != 1 && i != n) 32 ans[i] = base << 1; 33 else 34 ans[i] = base; 35 } 36 for (int i = 1; i <= n && i <= MOD; ++i) 37 { 38 ans[i]++; 39 } 40 for (int i = n + 1; i <= MOD; ++i) 41 { 42 ans[2 * n - i]++; 43 } 44 for (int i = 1; i <= n; ++i) printf("%lld%c", ans[i], " "[i == n]); 45 } 46 return 0; 47 }
C:Flip the Bits
水。

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 int t, n; 6 7 int main() 8 { 9 scanf("%d", &t); 10 while (t--) 11 { 12 scanf("%d", &n); 13 if (n & 1) 14 { 15 puts("1"); 16 continue; 17 } 18 else 19 { 20 int ans = 1; 21 while ((n & 1) == 0 && n) 22 { 23 ++ans; 24 n >>= 1; 25 } 26 printf("%d ", ans); 27 } 28 } 29 return 0; 30 }
D:Magic Sticks
题意:有n * m 的矩形 每个矩形四条边,从这些边中选取一个边的集合,使得任意两条边不相交,并且每个矩形至少有一条边被选中
思路:
偶数 * 偶数
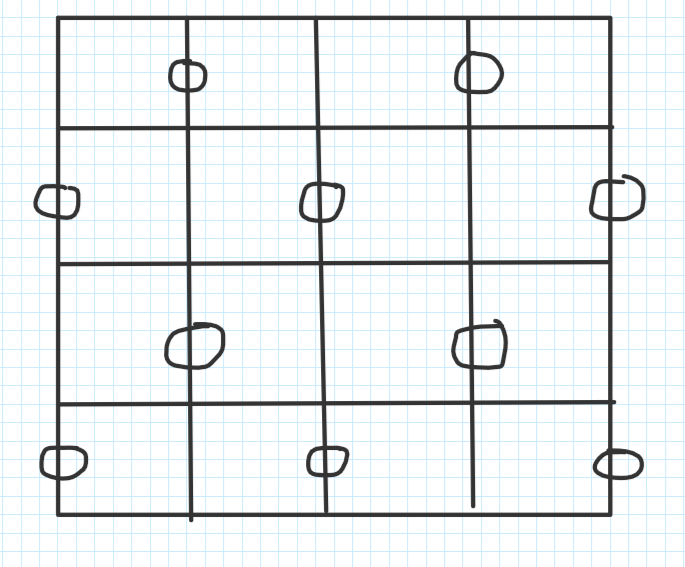
奇数 * 奇数
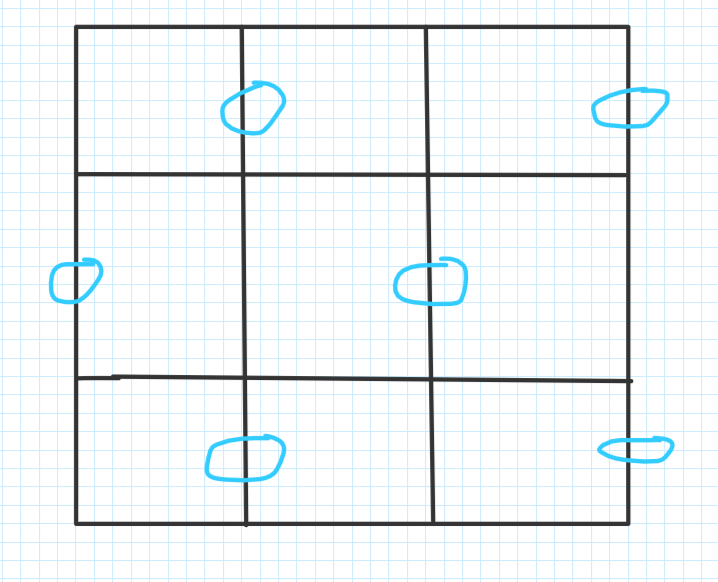
奇数 * 偶数
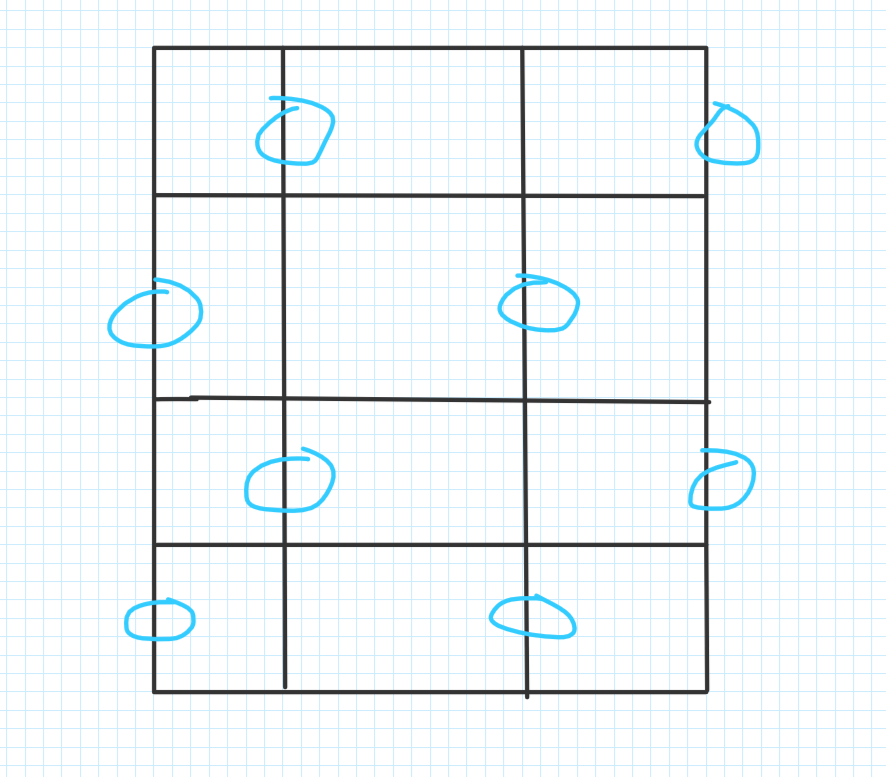
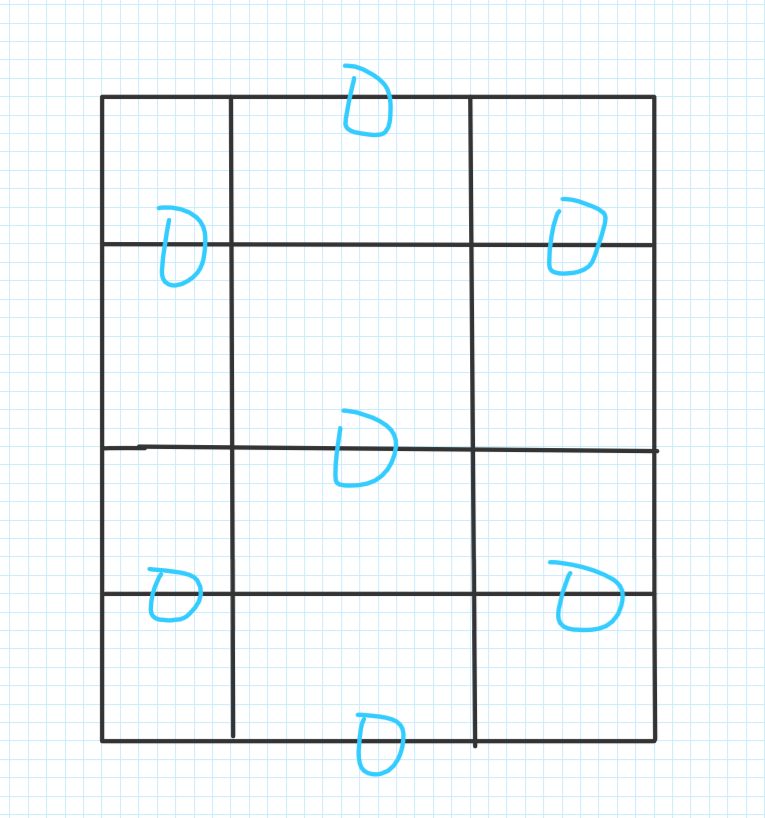

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define ll long long 6 7 #define INFLL 0x3f3f3f3f3f3f3f3f 8 9 int t; 10 ll n, m; 11 12 int main() 13 { 14 scanf("%d", &t); 15 while (t--) 16 { 17 scanf("%lld%lld", &n, &m); 18 19 ll ans = INFLL; 20 21 if (n % 2 == 0 && m % 2 == 0) 22 { 23 ans = min(ans, (n / 2) * (m + 1)); 24 ans = min(ans, (m / 2) * (n + 1)); 25 } 26 else if (n % 2 == 1 && m % 2 == 1) 27 { 28 ans = min(ans, ((n + 1) / 2) * m); 29 ans = min(ans, ((m + 1) / 2) * n); 30 } 31 else 32 { 33 if (n % 2 == 0) swap(n, m); 34 ans = min(ans, ((n + 1) / 2 * m)); 35 ans = min(ans, ((n + 1) / 2) * (m / 2) + (n / 2) * (m + 2) / 2); 36 } 37 printf("%lld ", ans); 38 } 39 return 0; 40 }
E:N - Dimensional Grid
题意: 在n维的空间,给你每个空间的长度,求有多少个格子相邻
思路:
一维:a1 - 1
二维:(a1 - 1) * a2 + (a2 - 1) * a1
大胆推广到高维:(a1 - 1) * (a2 + ... + an) + (a2 - 1) * (a1 + a3 + ... + an) ...
然后前缀后缀搞一搞

1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 typedef long long ll; 6 7 const int MOD = 1e9 + 7; 8 #define N 100010 9 10 int t,n; 11 ll arr[N],brr[N],crr[N]; 12 13 int main() 14 { 15 scanf("%d",&t); 16 while(t--) 17 { 18 scanf("%d",&n); 19 for(int i = 1; i <= n; ++i) 20 { 21 scanf("%lld",&arr[i]); 22 } 23 brr[0] = 1; 24 for(int i = 1; i <= n; ++i) 25 { 26 brr[i] = (brr[i - 1] * arr[i]) % MOD; 27 } 28 crr[n + 1] = 1; 29 for(int i = n; i >= 1; --i) 30 { 31 crr[i] = (crr[i + 1] * arr[i]) %MOD; 32 } 33 ll ans = 0; 34 for(int i = 1; i <= n; ++i) 35 { 36 ans = (ans + brr[i - 1] * (arr[i] - 1) %MOD * crr[i + 1] %MOD) %MOD; 37 } 38 printf("%lld ",ans); 39 } 40 return 0; 41 }
F:Minimum Sum of Array
题意:给出n个数,如果ai 可以整除aj,那么 ai 可以变成aj,求尽可能变换后,所有数的总和最小
思路:显然,贪心的想法是,对于每个数我们都给它变成这个数列中它跟它不互素的最小数,用类似素数筛法的思想去筛

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define N 100010 6 7 #define M 1000010 8 9 #define ll long long 10 11 int t, n; 12 int arr[N]; 13 int vis[M]; 14 int used[M]; 15 16 int main() 17 { 18 scanf("%d", &t); 19 while (t--) 20 { 21 scanf("%d", &n); 22 for (int i = 1; i <= n; ++i) 23 scanf("%d", arr + i); 24 sort(arr + 1, arr + 1 + n); 25 for (int i = 1; i <= arr[n]; ++i) 26 vis[i] = i, used[i] = 1; 27 for (int i = 1; i <= n; ++i) 28 { 29 int v = arr[i]; 30 if (v >= (arr[n] / 2 + 2)) break; 31 if (vis[v] == v && used[v] == 1) 32 { 33 used[v] = 0; 34 for (int j = v * 2; j <= arr[n]; j += v) 35 vis[j] = min(vis[j], v); 36 } 37 } 38 ll ans = 0; 39 for (int i = 1; i <= n; ++i) ans += vis[arr[i]]; 40 printf("%lld ", ans); 41 } 42 return 0; 43 }
G:Power of String
题意:给出一个式子,求修改最多k个字符,使得这个式子的值最大
思路:根据这个式子,我们可以知道假如一个字符有n个,那么这n个字符的值是(n * (n - 1)) / 2 * ASCII(ch)
那么我们可以把所有字符放在一起看
贪心的想法,如果存在答案,肯定是若干个小于等于k个字符变成同一个字符,因为这样会使得式子更大
那么我们枚举26个字符,使这个字符使要变成的字符
然后我们考虑,尽量让个数小的去换掉,那么个数小于等于k的字符就可以去做01背包,然后再枚举26位来当做补充

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define READ freopen("Test.in", "r", stdin); 6 #define N 100010 7 #define M 5010 8 #define ll long long 9 #define INFLL 0x3f3f3f3f3f3f3f3f 10 11 int t, n, K; 12 char s[N]; 13 14 ll num[200]; 15 16 inline ll F(ll x) 17 { 18 return (x * (x - 1)) / 2; 19 } 20 21 inline ll Get(char c, ll pre, ll now) 22 { 23 ll res = 0; 24 res = F(now) * c; 25 res -= F(pre) * c; 26 return res; 27 } 28 29 ll dp[M]; 30 ll f[M]; 31 32 inline ll work(char c) 33 { 34 for (int i = 1; i <= K; ++i) f[i] = -INFLL; 35 for (int i = 'a'; i <= 'z'; ++i) 36 { 37 if (i == c) continue; 38 if (num[i] == 0) continue; 39 dp[0] = 0; 40 for (int j = 1; j <= K; ++j) dp[j] = -INFLL; 41 for (int j = 'a'; j <= 'z'; ++j) 42 { 43 if (j == c || j == i) continue; 44 for (int l = K; l >= num[j]; --l) 45 dp[l] = max(dp[l], dp[l - num[j]] + Get(j, num[j], 0)); 46 } 47 ll tot = num[i]; 48 for (int j = K; j >= 0; --j) 49 { 50 if (tot + j <= K) 51 dp[tot + j] = max(dp[tot + j], dp[j] + Get(i, tot, 0)); 52 else 53 dp[K] = max(dp[K], dp[j] + Get(i, tot, tot - K + j)); 54 } 55 for (int j = 1; j <= K; ++j) f[j] = max(f[j], dp[j]); 56 } 57 ll res = 0; 58 for (int i = 1; i <= K; ++i) 59 res = max(res, f[i] + Get(c, num[c], num[c] + i)); 60 return res; 61 } 62 63 int main() 64 { 65 #ifdef LOCAL 66 READ; 67 #endif 68 scanf("%d", &t); 69 while (t--) 70 { 71 scanf("%d%d", &n, &K); 72 scanf("%s", s); 73 memset(num, 0, sizeof num); 74 for (int i = 0; s[i]; ++i) 75 num[s[i]]++; 76 ll ans = 0, tmp = 0; 77 for (int i = 'a'; i <= 'z'; ++i) 78 ans += F(num[i]) * i; 79 tmp = ans; 80 for (int i = 'a'; i <= 'z'; ++i) 81 ans = max(ans, tmp + work(i)); 82 printf("%lld ", ans); 83 } 84 return 0; 85 }
H:Making Friends
水。

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define N 2010 6 7 int t, n; 8 9 int arr[N]; 10 11 int main() 12 { 13 scanf("%d", &t); 14 while (t--) 15 { 16 scanf("%d", &n); 17 for (int i = 1; i <= n * 2; ++i) 18 scanf("%d", arr + i); 19 int ans = 0; 20 for (int i = 1; i <= n; ++i) 21 ans = max(ans, arr[i] + arr[2 * n - i + 1]); 22 printf("%d ", ans); 23 } 24 return 0; 25 }
I: Split the Number
水。

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 int t, x, n; 6 7 int main() 8 { 9 scanf("%d", &t); 10 while (t--) 11 { 12 scanf("%d%d", &x, &n); 13 if (x < n) 14 { 15 puts("-1"); 16 continue; 17 } 18 int base = x / n; 19 int MOD = x % n; 20 for (int i = 1; i <= n; ++i) 21 { 22 printf("%d%c", base + ((n - i + 1 <= MOD) ? 1 : 0), " "[i == n]); 23 } 24 } 25 return 0; 26 }
J:T-Shirts Dilemma
题意:给出 a b v 在a - b 中找出一个连续子区间,使得这个区间内的所有数按位或运算的和小于v 找出子区间的最大长度
思路:
我们可以从最高有效位往最低有效为看 用 vi 表示 v 的第i位 ai bi 同理
如果vi == 0 && ai == 0 && bi == 0 那么我们跳到下一位继续看
如果vi == 1 && ai == 0 && bi == 0 那么答案就是 b - a + 1 因为 将a - b 的所有数按位或起来的值肯定小于 v' (v' = 将v的第i位边为0, 小于i的所有位都变为1) 并且 v' < v
如果 vi == 0 && ai == 0 && bi == 1
那么我们可以将bi 变为0 然后将小于i的b的所有位都变为1 再往下一位看 这样的操作相当于缩小了b的范围,对答案没有影响
如果vi == 1 && ai == 1 && bi == 1
显然 我们可以将 vi ai bi 都变为0 然后看下一位操作 是没有影响的
如果vi == 0 && ai == 1 && bi == 1 那么此时答案显然为0 因为a > v
如果vi ==1 && ai == 0 && bi == 1
如果此时 vi的低位都为1 那么答案就是 b - a + 1
如果不是 我们可以 令c = 将vi 变为0 然后所有低位都变为1 答案为 c - a + 1
或者 我们 可以将 a 变成 c + 1 然后 三个数的第i位都变为0 继续找下去
为什么将a 变成 c + 1 而不考虑 c + 1 一下的数
因为 c | c + 1 必然大于等于v 而 等于的情况 就是 b - a + 1 已经特判过

1 #include <bits/stdc++.h> 2 3 using namespace std; 4 5 #define ll long long 6 7 int t; 8 9 ll a, b, v; 10 11 inline ll work(ll a, ll b, ll v, int i) 12 { 13 if (i == -1) 14 return 1ll; 15 16 ll D = (1ll << i) - 1; 17 18 bool ai = a & (D + 1), bi = b & (D + 1), vi = v & (D + 1); 19 20 if (vi && !ai && !bi) 21 return b - a + 1; 22 if (!vi && ai && bi) 23 return 0; 24 if (vi && ai && bi) 25 return work(a & D, b & D, v & D, i - 1); 26 if (!vi && !ai && !bi) 27 return work(a, b, v, i - 1); 28 if (!vi && !ai && bi) 29 return work(a, (1ll << i) - 1, v, i - 1); 30 31 if (v == ((1ll << (i + 1)) - 1)) 32 return b - a + 1; 33 34 ll c = (1ll << i) - 1; 35 return max(c - a + 1, work(0, b & D, v & D, i - 1)); 36 } 37 38 int main() 39 { 40 #ifdef LOCAL 41 freopen("Test.in", "r", stdin); 42 #endif 43 scanf("%d", &t); 44 while (t--) 45 { 46 scanf("%lld%lld%lld", &a, &b, &v); 47 printf("%lld ", work(a, b, v, 60)); 48 } 49 return 0; 50 }
K:League of Demacia
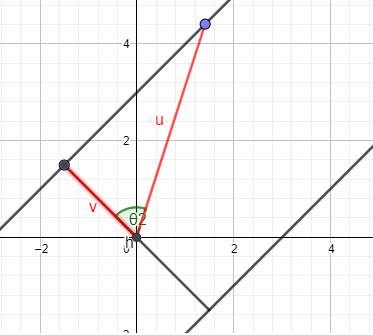
题意:给定一个原点,给定一条边长为z的线段,使得原点为中点,角度不定。从该线段两端点向同一方向画出两条射线,使得这一区域的点超过m个。
思路:显然我们可以枚举每一个点在射线上的情况,然后o(n)枚举每个点的情况。确定某一点是否在区域内可通过向量的数量积与z/2的比较以及向量积来确定是否为同一方向。

1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 #define N 1010 6 7 const double eps = 1e-8; 8 9 inline int sgn(double x) 10 { 11 if(fabs(x) < eps) return 0; 12 else if(x > 0) return 1; 13 else return -1; 14 } 15 16 struct Point{ 17 double x, y; 18 inline Point(){} 19 inline Point(double x, double y) : x(x), y(y){} 20 21 inline void input() 22 { 23 scanf("%lf %lf",&x, &y); 24 } 25 26 inline Point operator - (const Point &b) const 27 { 28 return Point(x - b.x, y - b.y); 29 } 30 31 inline double operator ^ (const Point &b) const 32 { 33 return x * b.y - y * b.x; 34 } 35 36 inline double operator * (const Point &b) const 37 { 38 return x * b.x + y * b.y; 39 } 40 41 inline Point operator + (const Point &b) const 42 { 43 return Point(x + b.x, y + b.y); 44 } 45 46 inline Point operator / (const double &k) const 47 { 48 return Point(x / k, y / k); 49 } 50 51 inline double distance(const Point &b) const 52 { 53 return hypot(x - b.x, y - b.y); 54 } 55 56 inline Point rotate(Point p, double angle) 57 { 58 Point v = (*this) - p; 59 double c = cos(angle), s = sin(angle); 60 return Point(p.x + v.x * c - v.y * s, p.y + v.x * s + v.y * c); 61 } 62 }P[N]; 63 64 int n, m; 65 double z; 66 67 int main() 68 { 69 int t; 70 scanf("%d",&t); 71 while(t--) 72 { 73 scanf("%d %d %lf",&n, &m, &z); 74 double r = z / 2; 75 for(int i = 1; i <= n; ++i) 76 { 77 P[i].input(); 78 } 79 bool flag = false; 80 for(int i = 1; i <= n; ++i) 81 { 82 Point a = P[i]; 83 double d = a.distance(Point(0, 0)); 84 if(sgn(d) == 0) a = Point(1, 0); 85 else if(sgn(d - r) <= 0) a = P[i]; 86 else a = P[i].rotate(Point(0, 0), acos(r / d)); 87 88 a = a / a.distance(Point(0, 0)); 89 int cnt = 1; 90 for(int j = 1; j <= n; ++j) 91 { 92 if(i == j) continue; 93 double tmp = fabs(P[j] * a); 94 if(sgn(tmp - r) <= 0 && sgn(a ^ P[j]) <= 0) cnt++; 95 if(cnt >= m) break; 96 } 97 if(cnt >= m) 98 { 99 flag = true; 100 break; 101 } 102 } 103 puts(flag ? "Yes" : "No"); 104 105 } 106 return 0; 107 }
L:Lazy Teacher
题意:对一个nm的矩阵填色,一共有k个颜色,相邻的方块不能同一种颜色,求填色方案。
思路:首先注意到n很小,其次当我们按顺序填方格时,影响这一方格以及接下来的方格的只会是前5块,因此我们只用记录前5块方格即可。因此对于每一个长度为6的方块实际上最多用到6种颜色,我们将其离散化后,那么最远的方块p1<1,p2<2,p3<3,p4<4,p5<5
然后我们可以枚举当前要填充颜色的方块的颜色,从0-5,其中5代表和前面5块互不相同个颜色,然后搜索一下(或者说dp?),最后剪剪枝。

1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 typedef long long ll; 6 7 const int MOD = 1e9 + 7; 8 9 #define M 10010 10 11 int val[6], pos[6]; 12 ll dp[6][M][2][3][4][5]; 13 14 int limit; 15 int n, m, k; 16 17 inline void update() 18 { 19 memset(val, 0, sizeof val); 20 for (int i = 0, color = 1; i < 5; ++i) 21 { 22 if (val[pos[i]] != 0) 23 { 24 pos[i] = val[pos[i]] - 1; 25 } 26 else 27 { 28 val[pos[i]] = color; 29 pos[i] = color - 1; 30 color++; 31 } 32 } 33 } 34 35 inline ll solve(int x, int y, int p2, int p3, int p4, int p5) 36 { 37 if (x == n) return solve(0, y + 1, p2, p3, p4, p5); 38 if (y == m) return 1; 39 if (dp[x][y][p2][p3][p4][p5] != -1) return dp[x][y][p2][p3][p4][p5]; 40 int res = 0; 41 int up; 42 if (n == 5) 43 { 44 up = 0; 45 } 46 else if (n == 4) 47 { 48 up = p2; 49 } 50 else if (n == 3) 51 { 52 up = p3; 53 } 54 else if (n == 2) 55 { 56 up = p4; 57 } 58 else if (up = 1) 59 { 60 up = p5; 61 } 62 for (int color = 0; color < limit; ++color) 63 { 64 if (color == up && y != 0) continue;//up 65 if (color == p5 && x != 0) continue;//left 66 pos[0] = p2, pos[1] = p3, pos[2] = p4, pos[3] = p5, pos[4] = color; 67 update();//离散化 68 res = (res + (color == 5 ? k - 5 : 1) * solve(x + 1, y, pos[1], pos[2], pos[3], pos[4])) % MOD;//5 means new color 69 } 70 dp[x][y][p2][p3][p4][p5] = res; 71 return res; 72 } 73 74 int main() 75 { 76 int t; 77 scanf("%d", &t); 78 while (t--) 79 { 80 scanf("%d %d %d", &n, &m, &k); 81 limit = min(k, 6); 82 memset(dp, -1, sizeof dp); 83 ll ans = solve(0, 0, 0, 0, 0, 0); 84 printf("%lld ", ans); 85 } 86 return 0; 87 }
M:Greedy Pirate
题意:给出一棵树,n - 1条边,一条边上两个权值,然后每次询问u -> v 问 从 u - > v的最大花费,每条边可以走两次
思路:显然 答案是所有边权和减去 终点到LCA的权值和 减去 LCA 到 起点的权值和

1 #include<bits/stdc++.h> 2 3 using namespace std; 4 5 const int maxn = 100010; 6 const int DEG = 20; 7 8 typedef long long ll; 9 int n; 10 11 struct Edge{ 12 int to,nxt; 13 int w1,w2; 14 inline Edge(){} 15 inline Edge(int to,int nxt,int w1,int w2):to(to),nxt(nxt),w1(w1),w2(w2){} 16 }edge[maxn << 1]; 17 18 int head[maxn],tot; 19 20 inline void addedge(int u,int v, int w1, int w2) 21 { 22 edge[tot] = Edge(v,head[u],w1,w2); 23 head[u] = tot++; 24 } 25 26 int fa[maxn][DEG]; 27 ll dis1[maxn];// from fa 28 ll dis2[maxn];// to fa 29 int deg[maxn]; 30 31 void init() 32 { 33 tot = 0; 34 memset(dis1, 0, sizeof dis1); 35 memset(dis2, 0, sizeof dis2); 36 memset(head, -1, sizeof head); 37 } 38 39 inline void BFS(int root) 40 { 41 queue<int>q; 42 deg[root] = 0; 43 fa[root][0] = root; 44 q.push(root); 45 while(!q.empty()) 46 { 47 int tmp = q.front(); 48 q.pop(); 49 for(int i = 1; i < DEG; ++i) 50 { 51 fa[tmp][i] = fa[fa[tmp][i - 1]][i - 1]; 52 } 53 for(int i = head[tmp]; ~i; i = edge[i].nxt) 54 { 55 int v = edge[i].to; 56 if(v == fa[tmp][0]) continue; 57 dis1[v] = dis1[tmp] + edge[i].w1; 58 dis2[v] = dis2[tmp] + edge[i].w2; 59 deg[v] = deg[tmp] + 1; 60 fa[v][0] = tmp; 61 q.push(v); 62 } 63 } 64 } 65 66 int LCA(int u,int v) 67 { 68 if(deg[u] > deg[v]) swap(u, v); 69 int hu = deg[u], hv = deg[v]; 70 int tu = u; 71 int tv = v; 72 for(int det = hv - hu, i = 0; det; det >>= 1, ++i) 73 { 74 if(det & 1) 75 tv = fa[tv][i]; 76 } 77 if(tu == tv) return tu; 78 for(int i = DEG - 1; i >= 0; --i) 79 { 80 if(fa[tu][i] == fa[tv][i]) continue; 81 tu = fa[tu][i]; 82 tv = fa[tv][i]; 83 } 84 return fa[tu][0]; 85 } 86 87 int main() 88 { 89 int t; 90 scanf("%d",&t); 91 while(t--) 92 { 93 init(); 94 scanf("%d",&n); 95 ll sum = 0; 96 for(int i = 1; i < n; ++i) 97 { 98 int u, v, w1, w2; 99 scanf("%d %d %d %d",&u, &v, &w1, &w2); 100 sum += w1 + w2; 101 addedge(u, v, w1, w2); 102 addedge(v, u, w2, w1); 103 } 104 BFS(1); 105 int q; 106 scanf("%d",&q); 107 while(q--) 108 { 109 int u,v; 110 scanf("%d %d",&u,&v); 111 int root = LCA(u,v); 112 ll ans = sum - (dis2[v] - dis2[root] + dis1[u] - dis1[root]); 113 printf("%lld ",ans); 114 } 115 } 116 return 0; 117 }
