RMQ的定义:
RMQ是询问某个区间内的最值,主要以ST表的方式实现。
在一般的问题中,经常需要维护区间的最值,此时就可以使用RMQ来维护了。
ST表:
1.预处理
用动态规划的思想来实现,但不支持在线修改。
用dp[i][j]表示以i为起点,长度为2^j的区间的最值,也就是区间[i,i+2^j-1]的最值。
因为维护的是最值,所以一个区间的最值可以由两个小区间的最值组成(要求这两个小区间完全覆盖大区间);
转移:dp[i][j]=max/min{dp[i][j-1],dp[i+(1<<(j-1))][j-1]};表示区间[i,i+(1<<j)-1]的最值为区间[i,i+(1<<(j-1))-1]和区间[i+(1<<(j-1)),i+(1<<j)]这两个区间的最值。
初始化:dp[i][0]=val[i];
时间复杂度:O(NlogN);
图示:i+2^(j-1)-1属于前区间,i+2^(j-1)属于后区间。

2.询问
对于一个区间可以用两个区间来覆盖,所以只要知道这两个区间就可以通过预处理完了的dp数组求得最值。
先找出区间[x,y]的长度所对应的最大的2的幂,也就是求出一个最大的K,满足2^k<=n。
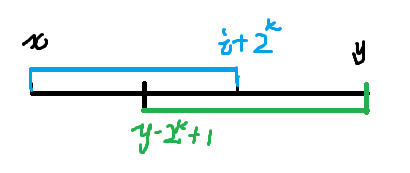
有了K之后可以将区间化为[x,x+(1<<k)],[y-(1<<k)+1,y]。
图示:
例题引入:
L2880 [USACO07JAN]平衡的阵容Balanced Lineup: https://www.luogu.org/problemnew/show/P2880
每天,农夫 John 的N(1 <= N <= 50,000)头牛总是按同一序列排队. 有一天, John 决定让一些牛们玩一场飞盘比赛. 他准备找一群在对列中为置连续的牛来进行比赛.
但是为了避免水平悬殊,牛的身高不应该相差太大. John 准备了Q (1 <= Q <= 180,000) 个可能的牛的选择和所有牛的身高 (1 <= 身高 <= 1,000,000). 他想知道每一组里面最高和最低的牛的身高差别.
例题解答:
模板题,直接用RMQ来维护每组里的Max和Min就行了。
代码:
#include<bits/stdc++.h> using namespace std; #define register int #define ll long long #define INF 0x3f3f3f3f #define maxn 50009 #define maxm inline ll read() { ll x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ll)(ch-'0');ch=getchar();} return x*f; } int dp[maxn][20],f[maxn][20]; int n,m,k,ans,tot; int main() { // freopen(".in","r",stdin); // freopen(".out","w",stdout); // memset(f,INF,sizeof(f)); n=read(),m=read(); for(int i=1;i<=n;i++) { int x=read(); dp[i][0]=x,f[i][0]=x; } for(int j=1;(1<<j)<=n;j++) for(int i=1;i+(1<<j)-1<=n;i++) { dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]); f[i][j]=min(f[i][j-1],f[i+(1<<(j-1))][j-1]); } for(int i=1;i<=m;i++) { int x=read(),y=read(); int k=log(y-x+1)/log(2); printf("%d ",max(dp[x][k],dp[y-(1<<k)+1][k])-min(f[x][k],f[y-(1<<k)+1][k])); } fclose(stdin); fclose(stdout); return 0; }
习题报告:
L2471 [SCOI2007]降雨量 :https://www.luogu.org/problemnew/show/P2471
解题思路:
一道毒瘤题...毒得一批...
首先这题可以想到用东西维护区间的最大值,然后就是一批毒瘤的判断了。
由于年份递增,所以在询问的时候可以二分查找最后一个小于等于当前输入的X,Y年的下标,(请默认X<Y)
设当前找到的X下标为nowx,Y为nowy,X值表示为Vx,Y值表示为Vy。
1.X值和Y值都已知,区间[nowx+1,nowy-1]的最大值为mx
false:Vy>Vx||mx>=Vy
maybe:Vy>mx&&区间[nowx,nowy]之间没有未知降雨量的年份&&mx<Vy
maybe:Vy>mx&&区间[nowx,nowy]之间有未知降雨量的年份&&mx<Vy
2.X值已知,Y值未知,区间[nowx+1,nowy-1]的最大值为mx
false:mx>=Vx
maybe:mx<Vx&&区间有未知年份
3.X值未知,Y值已知,区间[nowx,nowy-1]的最大值为mx
false:Vy<=mx
maybe:Vy>mx&&区间有未知年份
4.X值,Y值都未知
只有maybe

#include<bits/stdc++.h> using namespace std; #define re register int #define ll long long #define INF 0x3f3f3f3f #define maxn 50009 #define maxm inline ll read() { ll x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ll)(ch-'0');ch=getchar();} return x*f; } int n,m,k,ans,tot,Q,cnt; int dp[maxn<<1][25],year[maxn<<1]; int Query(int x,int y) { if(y<x) return -INF; int k=log2((double)y-x+1); return max(dp[x][k],dp[y-(1<<k)+1][k]); } int main() { // freopen(".in","r",stdin); // freopen(".out","w",stdout); n=read(); for(int i=1;i<=n;i++) year[i]=read(),dp[i][0]=read(); for(int j=1;(1<<j)<=n;j++) for(int i=1;i+(1<<j)-1<=n;i++) dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]); m=read(); for(int i=1;i<=m;i++) { int s=read(),t=read(); int f,nowx,nowy,mx; bool havx,havy; nowx=lower_bound(year+1,year+1+n,s)-year,//查找年份为s的下标 nowy=lower_bound(year+1,year+1+n,t)-year;// y havx=(s==year[nowx]&&nowx<=n),havy=(t==year[nowy]&&nowy<=n); //havx若为1则表明第x年的降水量已知,反之为未知 //havy同havx if(havx)//已知x值 { if(havy)//已知x值和y值 { mx=Query(nowx+1,nowy-1);//x值和y值已知,只需要查询 x+1->y-1的最值 if(dp[nowy][0]<=mx||dp[nowy][0]>dp[nowx][0])//x的值<y的值||y值<=mx为false f=0; else if(dp[nowy][0]>mx)// y值>mx,可能为true { if(nowy-nowx==t-s)//中间没有年份未知,为true f=1; else//有年份未知,为maybe f=2; } } else//x值已知,y值未知 { mx=Query(nowx+1,nowy-1);//虽然只是已知x,y还未知,但查询x+1->y-1和x值比较 if(dp[nowx][0]>mx)//mx<x值,maybe f=2; else//mx>=x值为false f=0; } } else//未知x值 { if(havy)//未知x值,已知y值 { mx=Query(nowx,nowy-1);//查询x->y-1的最值与y值进行比较 if(dp[nowy][0]<=mx)//y值<=mx 为false f=0; else//为maybe f=2; } else//x值,y值都未知,一定为maybe f=2; } if(f==2) puts("maybe"); else if(f==0) puts("false"); else puts("true"); } fclose(stdin); fclose(stdout); return 0; }
