Tarjan求强连通分量 缩点

强连通分量的定义：

　　在一张有向图中,如果两个点u,v之间能相互到达则称这两个点u,v是强连通的，在这个基础上如果有向图G中的任意两个顶点都强连通，那么称图G是一个强连通图。有向非强连通图的极大强连通子图称为强连通分量。极大强连通子图就是强连通子图中最大的那个，它不被其他强连通子图所包括。

　　概念挺多，特别混乱的感觉。理一下...

　　一个强连通图中的每一对顶点都必须强连通。

　　一个强连通图不叫做强连通分量，只叫做强连通图。

　　一个强连通子图G若为强连通分量那么必然是一个最大的强连通子图，也就是原图中不存在另一个图G'，使得G是G'的真子集。

　　举个例子:

　　

　　在图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达，子图{1,3,4}是一个强连通子图并不是强连通分量，因为它被子图{1,2,3,4}所包含，所以只是一个强连通子图。

强连通分量的应用：

　 　缩点：在一个有向图中将所有的强连通分量都缩成一个点的话，原图就会变成一个DAG(有向无环图)，因为DAG有一些比较好的性质，所以会给解题带来很大的方便。

　　　举个例子：

　　　　原图：

　　

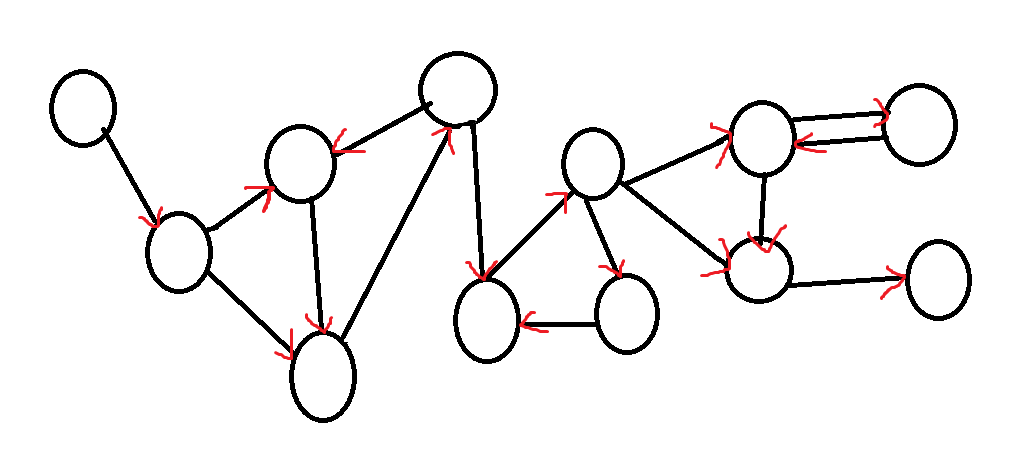
　　找出图中所有的强连通分量：

　　

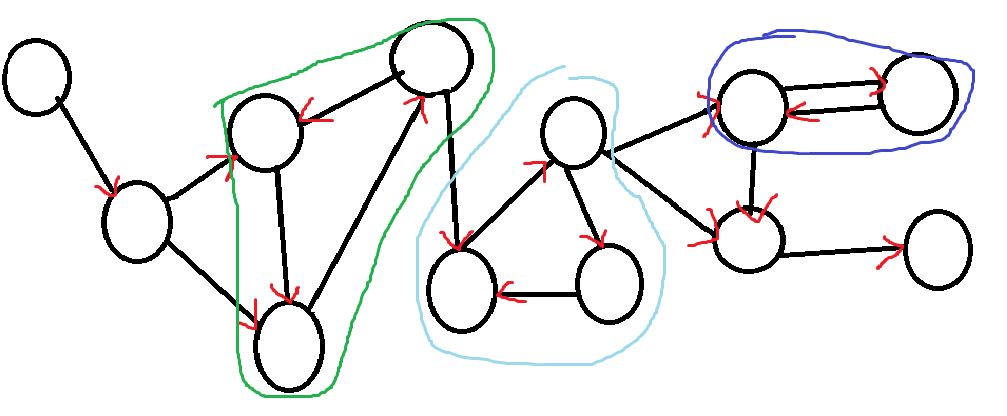
　　缩完点之后：

　　

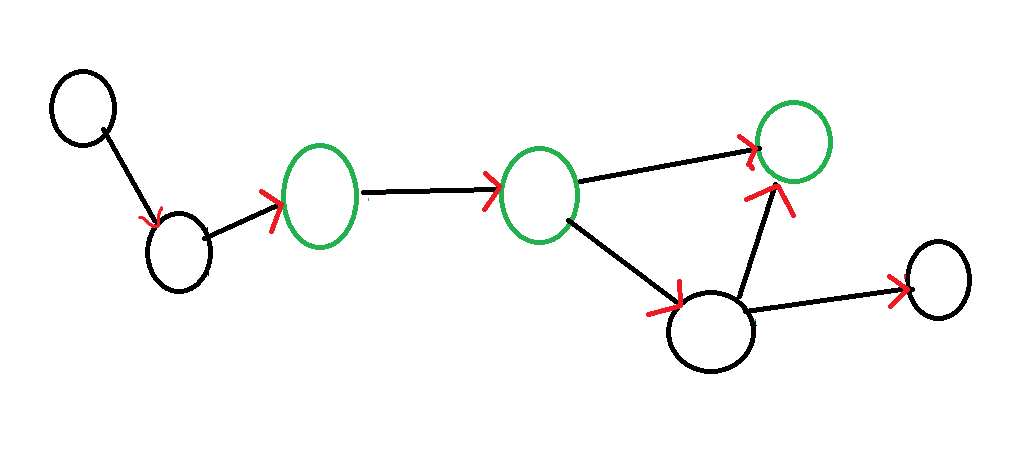
Tarjan 算法：

　　Tarjan算法以dfs的方式实现，每个强连通分量为搜索树中的一颗子树，搜索的时候，把当前搜索树中为处理的结点加入一个栈，回溯时可以判断到栈中的结点是否构成一个强连通分量。

　　 这个书面语不懂也罢，接着往下看吧。

　　 先介绍一下搜索时会遇到的四种边吧：

　　 树枝边：dfs时经过的边。

　　 前向边：与dfs方向一致，由某个结点指向其子孙的边。

　 　后向边：与dfs方向相反，有某个结点指向其祖先的边。

　　 横叉边：由某个结点指向搜索树种另一子树的边。

　　 dfn[u]: 表示结点u的搜索次序编号，也就是时间戳.

　　 low[u]: 表示结点u或u的子树能够回溯到的最早的栈中结点的时间戳(dfn)。

　　如果(u,v)为树枝边，u为v的父结点：low[u]=min(low[u],low[v]);

　　如果(u,v)为后向边或者指向栈中结点的横叉边:low[u]=min(low[u],dfn[v])；

　　指向栈中的结点的横叉边的原因是：一个点只能属于一个强连通分量，如果不是指向栈中结点的横叉边，那么横叉边的另一结点v一定在此之前已经属于了另一个强连通分量。

　　当结点u的搜索过程结束之后,如果dfn[u]=low[u]，那么以u为根的搜索子树上所有还在栈中的结点（即u和栈中在u之后的结点）是一个强连通分量，即可推栈。

　　因为当dfn[u]=low[u]时表示u即u的子孙结点最早能够到达的点便是结点u，那么u就是它的子孙中的最高祖先。

　　算法演示见博客：https://www.cnblogs.com/five20/p/7594239.html

例题：

　　#10091. 「一本通 3.5 例 1」受欢迎的牛: https://loj.ac/problem/10091

　　 解题思路：

　　由题意可得，一头牛u若为受欢迎的牛，那么他必然受到其他所有牛的喜欢，由于喜欢可以传递，那么意味着从其他的任一头牛出发都能到达牛u，也可得到一个环上的牛都是互相喜欢的，

所以把每个强连通子图找出来，缩点，然后整个图就变成了DAG，又因为一头牛要受到其他所有牛的喜欢，那么它不能喜欢除了自己这个联通块外的牛(图中已经不存在环了),所以这时只需要

统计一下出度为0的牛的个数，或者直接建反向边，改为统计入度为0的牛的个数。

　　最后注意缩点后连通块数目多于一个的情况，此时因为联通快多于1个且互不连通，导致没有牛可以收到其他所有牛的喜欢了。

#include<bits/stdc++.h>
using namespace std;
#define INF 0x3f3f3f3f
#define ll long long
#define maxn 50009
inline ll read()
{
    ll x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')    f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ll)(ch-'0');ch=getchar();}
    return x*f;
}
int head[maxn],belong[maxn],low[maxn],dfn[maxn],in[maxn];
struct edge
{
    int to,nxt;
}p[maxn];
bool vis[maxn];
stack<int> s;
int n,m,k,cnt,tot,now,ans,id,sum;

void add(int x,int y)
{
    ++cnt,p[cnt].to=y,p[cnt].nxt=head[x],head[x]=cnt;
}

void Tarjan(int u)
{
    dfn[u]=++id;
    low[u]=dfn[u];
    s.push(u);
    vis[u]=1;
    for(int i=head[u];i;i=p[i].nxt)
    {
        int v=p[i].to;
        if(!dfn[v])
        {
            Tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(!belong[v])
        {
            low[u]=min(low[u],dfn[v]);
        }
    }
    if(dfn[u]==low[u])
    {
        tot++;
        while(1)
        { 
            int v=s.top();
            belong[v]=tot;   
            s.pop();
            vis[v]=0;
            if(u==v)
                break; 
        }
    }
}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read(),m=read();
    for(int i=1;i<=m;i++)
    {
        int x=read(),y=read();
        add(y,x);//建反边，可以将统计连通块的出度转化为统计连通块的入度 
    }
    
    for(int i=1;i<=n;i++)
    {
        if(!dfn[i])
            Tarjan(i);
    }
    for(int i=1;i<=n;i++)
        for(int j=head[i];j;j=p[j].nxt)
        {
            int v=p[j].to;
            if(belong[i]!=belong[v])
                in[belong[v]]++;
        }
    for(int i=1;i<=tot;i++)
        if(in[i]==0)
        {
            now=i;
            sum++;
        }
    if(sum!=1)
        puts("0");
    else
    {
        sum=0;
        for(int i=1;i<=n;i++)
            if(belong[i]==now)
                sum++;
        printf("%d
",sum);    
    }
//    fclose(stdin);
//    fclose(stdout);
    return 0;  
}
/* 
6 8
1 2
1 3
2 4
3 4
3 5
4 1
4 6
5 6
*/

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define ll long long
#define INF 0x3f3f3f3f
#define maxn 10009
#define maxm  50009
inline ll read()
{
    ll x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=(x<<1)+(x<<3)+(ll)(ch-'0');ch=getchar();}
    return x*f;
}
int head[maxn],s[maxn],belong[maxn],dfn[maxn],low[maxn],in[maxn];
int n,m,k,ans,tot,cnt,sum,id,top,block;
struct edge
{
    int to,nxt;
}p[maxm];

void add(int x,int y)
{
    p[++cnt]={y,head[x]},head[x]=cnt;
}

void Tarjan(int u)
{
    dfn[u]=low[u]=++id;
    s[++top]=u;
    for(int i=head[u];i;i=p[i].nxt)
    {
        int v=p[i].to;
        if(!dfn[v])
        {
            Tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(!belong[v])
            low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u])
    {
        ++block;
        while(1)
        {
            belong[s[top]]=block;
            if(s[top]==u)
                break;
            --top;
        }
        --top;
    }
}
int main()
{
//    freopen(".in","r",stdin);
//    freopen(".out","w",stdout);
    n=read(),m=read();
    for(int i=1;i<=m;i++)
    {
        int x=read(),y=read();
        add(y,x);
    }
    for(int i=1;i<=n;i++)
        if(!dfn[i])
            Tarjan(i);
/*    for(int i=1;i<=n;i++)
        cout<<belong[i]<<" ";
    cout<<endl;*/
    for(int u=1;u<=n;u++)
        for(int i=head[u];i;i=p[i].nxt)
        {
            int v=p[i].to;
            if(belong[u]!=belong[v])
                in[belong[v]]++;
        }
    int now;
    for(int i=1;i<=block;i++)
        if(in[i]==0)
            ans++,now=i;
    if(ans!=1)
    {
        puts("0");
        return 0;
    }
    ans=0;
    for(int i=1;i<=n;i++)
        if(belong[i]==now)
            ++ans;
    printf("%d
",ans);    
    fclose(stdin);
    fclose(stdout);
    return 0;
}