转自:
①:https://www.cnblogs.com/ECJTUACM-873284962/p/7620370.html
②:https://www.cnblogs.com/c1299401227/p/5349727.html
错排的定义:
一段序列中一共有$n$个元素,那么可知这些元素一共有$n!$种排列方法。假如在进行排列时,原来所有的元素都不在原来的位置,那么称这个排列为错排。而错排数所指的就是在一段有$n$个元素的序列中,有多少种排列方式是错排。
错排公式:
递归关系:$$D(n)=(n-1)(D(n-1)+D(n-2)) $$ 特别地有$D(1)=0$,$D(2)=1$;
错排公式:$$D(n)=(n!)[frac{(-1)^0}{0!}+frac{(-1)^1}{(1!)}+frac{(-1)^2}{(2!)}+frac{(-1)^3}{(3!)}+......+frac{(-1)^n}{(n!)}]$$; 其中$n!=n*(n-1)*(n-2)*......3*2*1 $ 特别地有$0!=1$ ,$1!=1$
递推关系推导:
$n$个不同的元素的一个错排公式可以分作两步完成:
第一步:假设我们错排第一个元素,那么它可以从$2->n$的位置任意选择其中的一个,一共是有n-1种选择。
第二步:错排其余$n-1$个元素,也是需要分情况和种类的。因为这需要看第一步的结果,如果第一个元素落在第$k$个位置上,第二步就需要把$k$号元素进行错排,$k$号元素错排位置的不同将导致不同的情况会发生:
1.假设$k$号元素正好落在了第一个元素的位置,那么就可以将第一个元素和第k个元素完全剔除出去,因为相当于只是他们两者互换了位置,其他元素暂时还没有发生变动。留下来的$n-2$元素进行错排的话,那么我们就可以得到了$D(n-2)$种的错排方式。
2.若$k$号元素不排到第一个元素的位置,我们可以暂时将现在排在k号位置的第一个元素剔除出去,生下来的就只包含k号元素和原来$n-2$个的元素了。这时,我们可以将原来的第一个元素的位置看做是现在k号元素的原本位置,因为k号元素不能够放在原来的位置上,所以就相当于是原来的$n-2$个元素和$k$共计$n-1$个元素进行完全的错排。那么一共就有$D(n-1)$种方法。 第二种情况希望大家仔细理解!配一张图便于理解
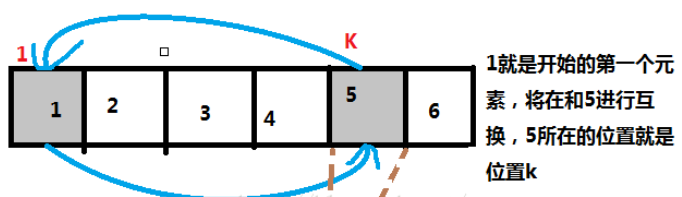

那么,我们有根据加法原理,完成第二步有$D(n-2)+D(n-1)$种方法。
根据乘法原理得到$D(n)=(n-1)(D(n-1)+D(n-2))$ 。递推关系解释完毕。
错排公式推导:
$$D(n) = (n-1) [D(n-2) + D(n-1)]$$
特殊地,$D(1) = 0$, $D(2) = 1$.
下面通过这个递推关系推导:
为方便起见,设$$D(k) = k! N(k), k = 1, 2, …, n$$
则$$N(1) = 0, N(2) = 1/2$$.
$n ≥ 3$时,$$n! N(n) = (n-1) (n-1)! N(n-1) + (n-1)! N(n-2)$$
即 $$nN(n) = (n-1) N(n-1) + N(n-2)$$
于是有$$N(n) - N(n-1) = $frac{- [N(n-1) - N(n-2)]}{n}$ =-frac{1}{n}) [-frac{1}{(n-1)}] [-frac{1}{(n-2)}]…(-frac{1}{3}) [N(2) - N(1)] = frac{(-1)^n} {n!}$$.
因此将
$$N(n)-N(n-1)=frac{(-1)^(n)}{(n!)}$$
$$N(n-1) - N(n-2) = frac{(-1)^(n-1)} {(n-1)!}$$
$$N(n-2)-N(n-3)=frac{(-1)^(n-2)}{(n-2)}
$$...$$
$$...$$
$$...$$
$$N(3)-N(2)=frac{(-1)^3}{3!}$$
$$N(2) - N(1) =frac{(-1)^2}{2!}$$
相加,可得
$$N(n) =frac{(-1)^2}{2!} + … + frac{(-1)^(n-1)}{(n-1)!} +frac{(-1)^n}{n!}$$
因此
$$D(n) = n! [frac{(-1)^2}{2!} + … + frac{(-1)^(n-1)}{(n-1)!} + frac{(-1)^n}{n!}]$$
此即错排公式。