LeetCode 894. All Possible Full Binary Trees

原题链接在这里：https://leetcode.com/problems/all-possible-full-binary-trees/

题目：

A full binary tree is a binary tree where each node has exactly 0 or 2 children.

Return a list of all possible full binary trees with N nodes.  Each element of the answer is the root node of one possible tree.

Each node of each tree in the answer must have node.val = 0.

You may return the final list of trees in any order.

Example 1:

Input: 7
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
Explanation:

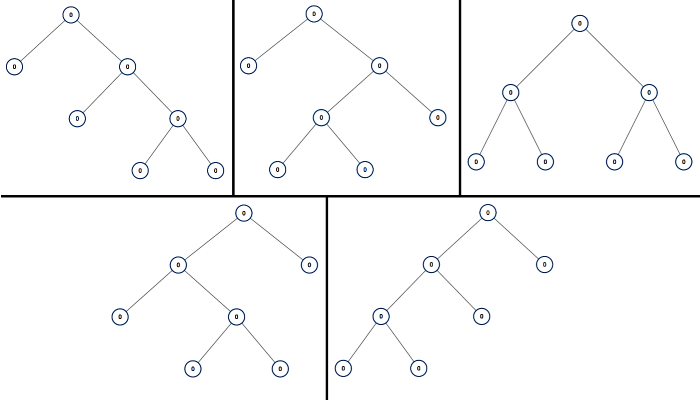
Note:

• 1 <= N <= 20

题解：

If we mark node from 0 to N-1.

Only the odd index node, like 1, 3, 5 could be root. Since count of nodes on left is odd and count of node on right is odd.

Even number of nodes can't form a full binary tree.

Could use recursive call to get a list of possible left subtrees, and a list of possible right subtrees.

For each of them, append it back to root, and add to res.

We could use cache to memorize results of N. Then no need to recalculate. 

Also it would be bebetter to deep clone the subtree, or in the future if one node is changed, all its reference would be changed too.

Time Complexity: O(n^3). T(N) = T(1)*T(N-2) + T(3)*T(N-4) + ... + T(N-2)*T(1). With Cache, when calculate T(N-2), all number smaller than N-2 is calculated and put into cache. Then for the rest, get T(i) from cache needs O(1) time. There could be O(N) results for subtrees, size of list could be O(N). Totoally, equation length is N/2, Then T(N) = N/2 * (N*N) = O(N^3).

Space: O(N^3). cache count is O(N). For each value, list size could be O(N). Within list, each tree could be O(N). Thus, it takes O(N^3) space.

AC Java:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    HashMap<Integer, List<TreeNode>> hm = new HashMap<Integer, List<TreeNode>>();
    
    public List<TreeNode> allPossibleFBT(int N) {
        if(hm.containsKey(N)){
            return hm.get(N);
        }
        
        List<TreeNode> res = new ArrayList<TreeNode>();
        if(N<1 || N%2 == 0){
            hm.put(N, res);
            return res;
        }
        
        if(N == 1){
            res.add(new TreeNode(0));
            hm.put(N, res);
            return res;
        }
        
        for(int i = 1; i<N; i+=2){
            List<TreeNode> left = allPossibleFBT(i);
            List<TreeNode> right = allPossibleFBT(N-1-i);

            for(TreeNode l : left){
                for(TreeNode r : right){
                    TreeNode root  = new TreeNode(0);
                    root.left = deepClone(l);
                    root.right = deepClone(r);
                    res.add(root);
                }
            }
        }
        
        hm.put(N, res);
        return res;
    }
    
    private TreeNode deepClone(TreeNode root){
        if(root == null){
            return root;
        }
        
        TreeNode copy = new TreeNode(root.val);
        copy.left = deepClone(root.left);
        copy.right = deepClone(root.right);
        return copy;
    }
}

类似Unique Binary Search Trees II.