LeetCode 787. Cheapest Flights Within K Stops

原题链接在这里：https://leetcode.com/problems/cheapest-flights-within-k-stops/

题目：

There are n cities connected by m flights. Each fight starts from city u and arrives at v with a price w.

Now given all the cities and flights, together with starting city src and the destination dst, your task is to find the cheapest price from srcto dst with up to k stops. If there is no such route, output -1.

Example 1:
Input: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
Output: 200
Explanation: 
The graph looks like this:

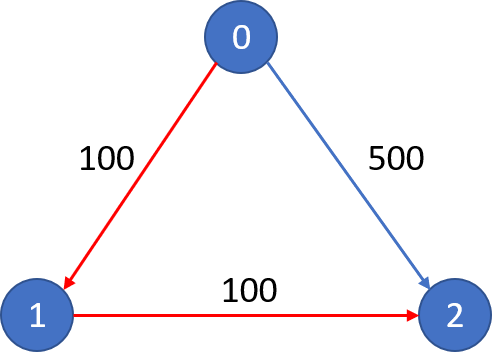
The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.

Example 2:
Input: 
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
Output: 500
Explanation: 
The graph looks like this:

The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.

Note:

• The number of nodes n will be in range [1, 100], with nodes labeled from 0 to n - 1.
• The size of flights will be in range [0, n * (n - 1) / 2].
• The format of each flight will be (src, dst, price).
• The price of each flight will be in the range [1, 10000].
• k is in the range of [0, n - 1].
• There will not be any duplicated flights or self cycles.

题解：

When it comes to Dijkstra, it needs PriorityQueue based on cost.

From the example, if the stops is within K, then it could continue update the total cost.

Create a map first. 

Initialize PriorityQueue based on current cost. Put src in it.

When polling out head node, check if it is dst, if it is, it must be smallest cost because of PriorityQueue.

Otherwise, get its stop, it is still smaller than K, and check the graph, get next nestinations and accumlate the cost, add to PriorityQueue.

If until the PriorityQueue is empty, there is no return yet, then there is no such route, return -1.

Time Complexity: O(ElogE). E = flights.length. que size could be E, each add and poll takes logE.

Space: O(E). graph size is O(E). que size is O(E).

AC Java: 

class Solution {
    public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {
        if(n == 0 || K < 0 || flights == null || flights.length == 0 || flights[0].length != 3){
            return -1;
        }
        
        int res = Integer.MAX_VALUE;
        
        Map<Integer, List<int []>> graph = new HashMap<>();
        for(int [] f : flights){
            if(!graph.containsKey(f[0])){
                graph.put(f[0], new ArrayList<int []>());
            }
            
            graph.get(f[0]).add(new int[]{f[1], f[2]});
        }
        
        PriorityQueue<Node> que = new PriorityQueue<Node>((a, b) -> a.cost-b.cost);
        que.add(new Node(src, 0, -1));
        while(!que.isEmpty()){
            Node cur = que.poll();
            
            if(cur.city == dst){
                return cur.cost;
            }
            
            if(cur.stop < K){
                List<int []> nexts = graph.getOrDefault(cur.city, new ArrayList<int []>());
                for(int [] next : nexts){
                    que.add(new Node(next[0], cur.cost+next[1], cur.stop+1));
                }
            }
        }
        
        return -1;
    }
}

class Node{
    int city;
    int cost;
    int stop;
    public Node(int city, int cost, int stop){
        this.city = city;
        this.cost = cost;
        this.stop = stop;
    }
}