记录B站yxc的背包九讲相关代码

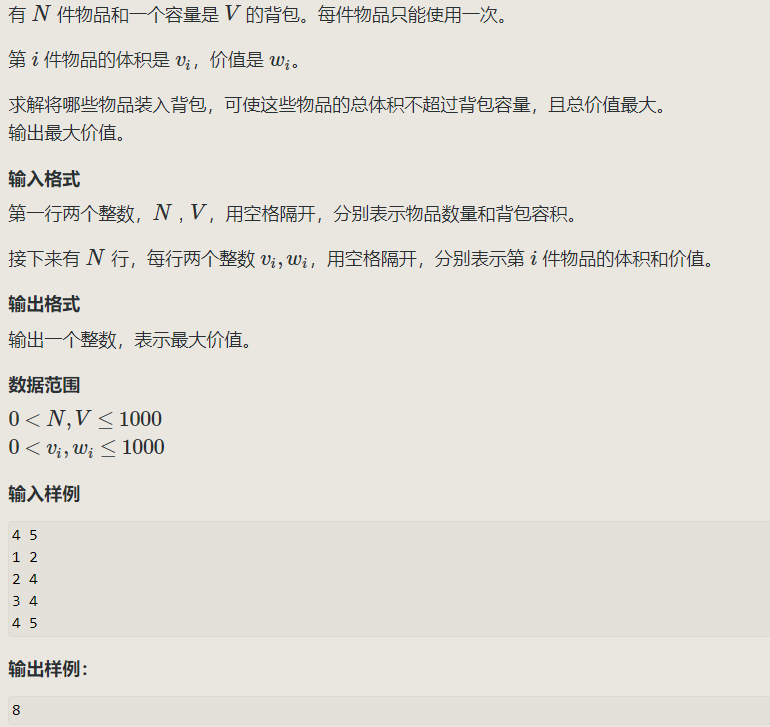
1.01背包

 

 

 

 

 

 

 

 

 

 

 

 

 

#include<iostream> 
#include <cstring> 
using namespace std; 

const int N = 1010; 
int f[N]; 

int main()
{
    int n,m; 
    while(cin >> n >> m){
        int v,w; 
        for (int i= 0 ; i < n;i++){
            cin >> v >> w; 
            for(int j = m; j >= v;j--){
                f[j] = max(f[j],f[j - v]+ w); 
            }
        }
        cout << f[m] << endl; 
    }
    return 0; 
}

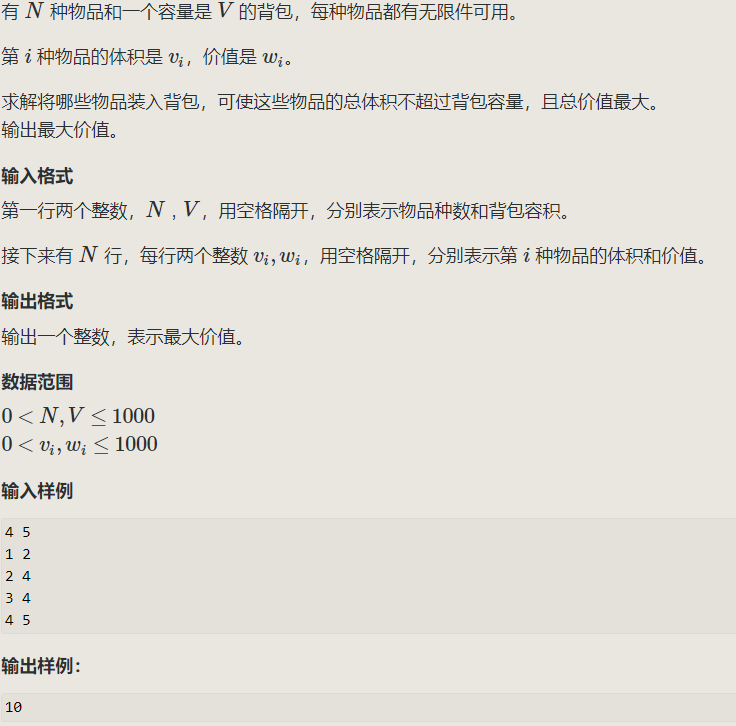
2.完全背包

#include<iostream>
#include <bits/stdc++.h>
using namespace std;
const int N = 1010;
int main()
{
	const int N = 1010;
	vector<int> dp(N);
	vector<int> v(N);
	vector<int> w(N);

	int n, m;
	cin >> n >> m;
	for (int i = 1; i <= n; i++)
	{
		cin >> v[i] >> w[i];
	}

	for (int i = 1; i <= n; i++)
		for (int j = v[i]; j <= m; j++)
		{
			dp[j] = max(dp[j], dp[j - v[i]] + w[i]);
		}
	cout << dp[m] << endl;
}

3.多重背包I

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
using namespace std; 

int n, m;
const int N = 110;
int f[N];
int main() {
	cin >> n >> m; 
	for (int i = 0; i < n; i++) {
		int v, w, s;
		cin >> v >> w >> s;
		for (int j = m; j >= 0; j--) {
			for (int k = 1; k <= s && k * v <= j; k++) {
				f[j] = max(f[j], f[j - k * v] + k * w);
			}
		}
	}
	cout << f[m] << endl;
	return 0;
}　

4.多重背包II （二进制优化版本）

#include <iostream> 
#include <algorithm> 
#include <cstring> 
#include <vector>
using namespace std; 

const int N = 2010; 
int f[N]; 

struct Goods
{
    int v; 
    int w; 
}; 


int main() {
        int n, m; 
        vector<Goods> goods;
        cin >> n >> m;
        for (int i = 0; i < n; i++) {
               int v, w, s;
               cin >> v >> w >> s;
               for (int k = 1; k <= s; k *= 2) {
                       s -= k;  
                       goods.push_back({ v * k,w * k });
               }
               if (s > 0) goods.push_back({ v * s,w * s }); // 如果 s还有剩余的
        }
        for (auto good : goods) {
               for (int j = m; j >= good.v; j--) {
                       f[j] = max(f[j], f[j - good.v] + good.w);  //转化为01背包
               }
        }
        cout << f[m] << endl;
        return 0;
}

5.混合背包

#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 1010;
int n, m;
int f[N];
struct Thing {
	int kind;
	int v, w;
};

vector<Thing> things;

int main() {
	cin >> n >> m;
	for (int i = 0; i < n; i++) {
		int v, w, s;
		cin >> v >> w >> s;
		if (s < 0) { things.push_back({ -1,v,w }); } // 背包情况
		else if (s == 0) {   // 完全背包
			things.push_back({ 0,v,w });
		}
		else { // 多重背包利用二进制优化转 01背包
			for (int k = 1; k <= s; k *= 2) {
				s -= k;
				things.push_back({ -1,k * v,k * w });
			}
			if (s > 0) {
				things.push_back({ -1,s * v,s * w });
			}
		}
	}
	for (auto thing : things) {
		if (thing.kind < 0) { // 01 背包从大到小遍历
			for (int j = m; j >= thing.v; j--) {
				f[j] = max(f[j], f[j - thing.v] + thing.w);
			}
		}
		else { // 完全背包，从小到大遍历
			for (int j = thing.v; j <= m; j++) {
				f[j] = max(f[j], f[j - thing.v] + thing.w);
			}
		}
	}
	cout << f[m] << endl;
	return 0;
}

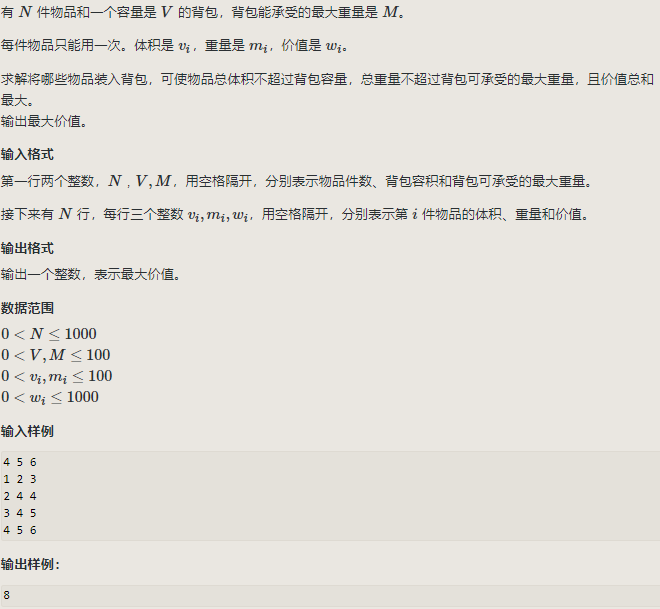
6.二维背包费用问题（两个约束——体积和重量约束）

#include <iostream>
#include<algorithm>
#include <cstring>

using namespace std; 
const int N = 110; 
int n, v, m; 
int f[N][N]; 

int main() {
	cin >> n >> v >> m; 
	for (int i = 0; i < n; i++) {
		int a, b, c; 
		cin >> a >> b >> c; 
		for (int j = v; j >= a; j--) {
			for (int k = m; k >= b; k--) {
				f[j][k] = max(f[j][k], f[j - a][k - b] + c); 
			}
		}
	}
	cout << f[v][m] << endl; 
	return 0; 
}

7.分组背包

#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std; 


const int N = 110; 
int f[N], v[N], w[N]; 

int n, m; 

int main() {
	cin >> n >> m; 
	for (int i = 0; i < n; i++) { // 循环物品组数
		int s; 
		cin >> s; // 当前组物品数量
		for (int j = 0; j < s; j++) {
			cin >> v[j] >> w[j];  // 当前组内物品数的体积和价值
		}
		for (int j = m; j >= 0; j--) { 
			for (int k = 0; k < s; k++) { // 同一组内的物品只能选一个
				if (j >= v[k]) {
					f[j] = max(f[j], f[j - v[k]] + w[k]); 
				}
			}
		}
	}
	cout << f[m] << endl; 
	return 0; 
}

8.有依赖的背包问题

 

 代码来源：https://www.acwing.com/solution/acwing/content/8316/ 

#include<iostream>
#include<vector>
using namespace std;
int f[110][110];//f[x][v]表达选择以x为子树的物品，在容量不超过v时所获得的最大价值
vector<int> g[110];
int v[110], w[110];  //物品的体积、价值和依赖的物品编号(父节点）
int n, m, root;
int dfs(int x)
{
        for (int i = v[x]; i <= m; i++) f[x][i] = w[x];//点x必须选，所以初始化f[x][v[x] ~  m]= w[x]
        for (int i = 0; i < g[x].size(); i++)
        {
               int y = g[x][i];
               dfs(y);
               for (int j = m; j >= v[x]; j--)//j的范围为v[x]~m, 小于v[x]无法选择以x为子树的物品
               {
                       for (int k = 0; k <= j - v[x]; k++)//分给子树y的空间不能大于j-v[x],不然都无法选根物品x
                       {
                              f[x][j] = max(f[x][j], f[x][j - k] + f[y][k]);
                       }
               }
        }
}
int main()
{
        cin >> n >> m;
        for (int i = 1; i <= n; i++)
        {
               int fa;
               cin >> v[i] >> w[i] >> fa;
               if (fa == -1)
                       root = i;
               else
                       g[fa].push_back(i);
        }
        dfs(root);
        cout << f[root][m];
        return 0;
}

9.背包问题求方案数

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
const int mod = 1e9 + 7;
int f[N];
int cnt[N];
int main() {
        int n, m;
        scanf("%d%d", &n, &m);
        for (int i = 0; i < n; i++) {
               cnt[i] = 1; //什么都不装也是一种方案
        }
        for (int i = 1; i <= n; i++) {
               int v, w;
               scanf("%d%d", &v, &w);// 体积和价值
               for (int j = m; j >= v; j--) {
                       int value = f[j - v] + w;
                       if (value > f[j]) {
                              f[j] = value;
                              cnt[j] = cnt[j - v];
                       }
                       else if (value == f[j]) {
                              cnt[j] = (cnt[j] + cnt[j - v]) % mod;
                       }
               }
        }
        printf("%d", cnt[m]);
        return 0;
}

10.背包问题求具体方案数

#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int f[N][N];
int v[N], w[N];
int n, m;
int main()
{
        cin >> n >> m;
        for (int i = 1; i <= n; i++)
               cin >> v[i] >> w[i];
        for (int i = n; i >= 1; i--)
        {
               for (int j = 0; j <= m; j++)
               {
                       f[i][j] = f[i + 1][j];
                       if (j >= v[i])
                              f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
               }
        }
        int cur_v = m;
        for (int i = 1; i <= n; i++)
        {   //如果是最后一个元素，特判一下，防止越界即可
               if (i == n && cur_v >= v[i])
               {
                       printf("%d ", i);
                       break;
               }
               if (cur_v <= 0)
                       break;
               //判断下标是否越界
               if (cur_v - v[i] >= 0 && f[i][cur_v] == f[i + 1][cur_v - v[i]] + w[i]) {
                       printf("%d ", i);
                       cur_v = cur_v - v[i];//选了第i个物品，剩余容量就要减小。
               }
        }
        return 0;
}