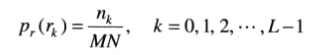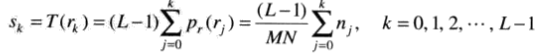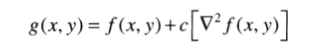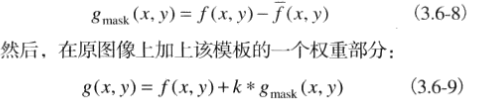灰度变换和空间滤波基础
图像增强例子
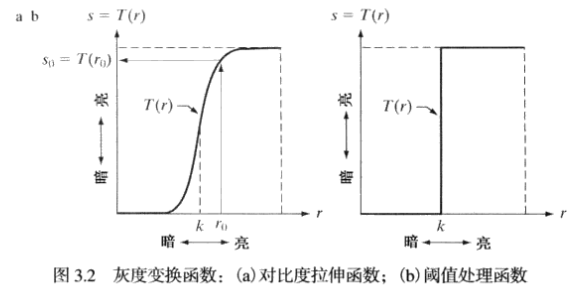
基本的灰度变换函数
<!-- more -->
图像反转
s = L - 1 - r
对数变换
s = c log (1 + r)
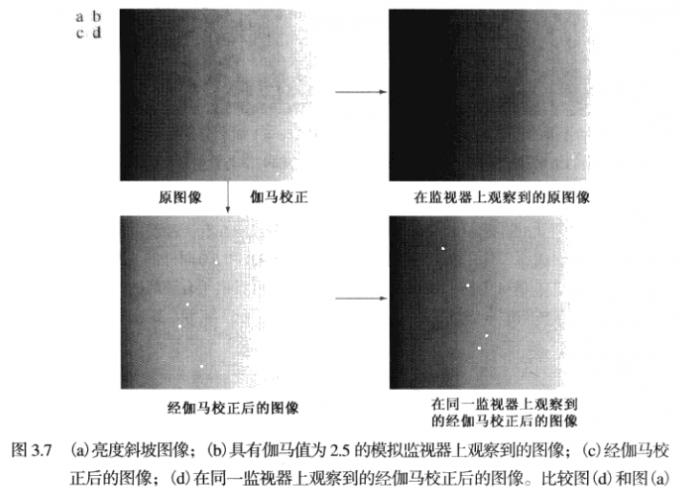
伽马变换 (改变对比度)
s = c r^y
改变伽马值不仅会改变亮度,而且会改变彩色图像中红、绿、蓝的比率。
分段线性变换
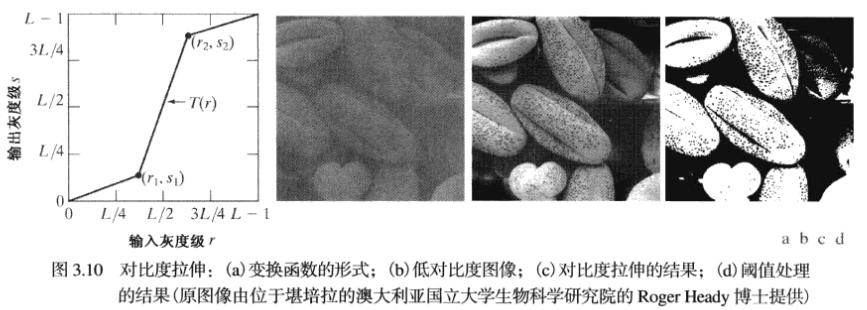
对比度拉伸
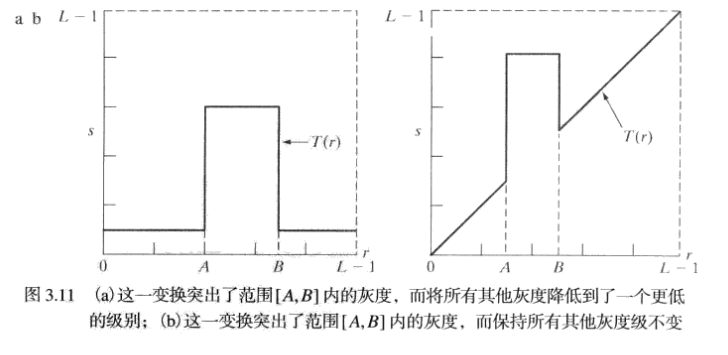
灰度级分层
(a)变换产生了一幅二值图像。(b)使感兴趣范围的灰度变亮(或变暗),而保持图像中其他灰度级不变。
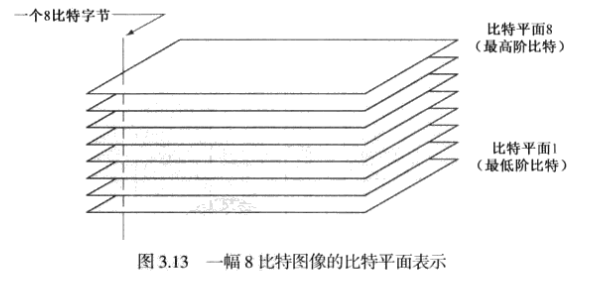
比特平面分层
256级灰度图像中,每个像素的灰度是由8比特(1个字节)组成。 一幅8比特图像由8个1比特平面组成,其中平面1包含图像中所有像素的最低阶比特,平面8包含图像中所有像素的最高阶比特。
直方图处理
直方图
其中,MN是图像中像素的总数,nk是灰度为rk的像素个数,L是图像中可能的灰度级的数量(即对8比特图像是256),rk相对的p(rk)图形通常称为直方图。
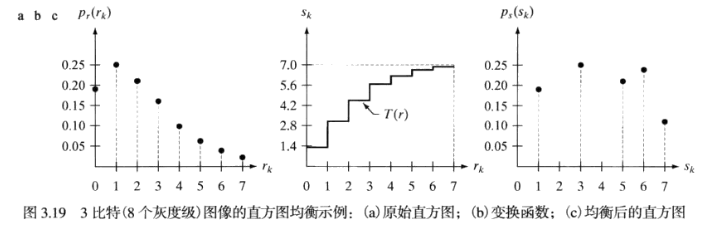
直方图均衡
将输入图像中灰度级为rk的各像素映射到输出图像中灰度级为sk的对应像素。
直方图均衡说明实例

图像具有相同内容,直方图均衡导致的对比度增强足以步长图像在视觉上难以区分灰度级的差别。
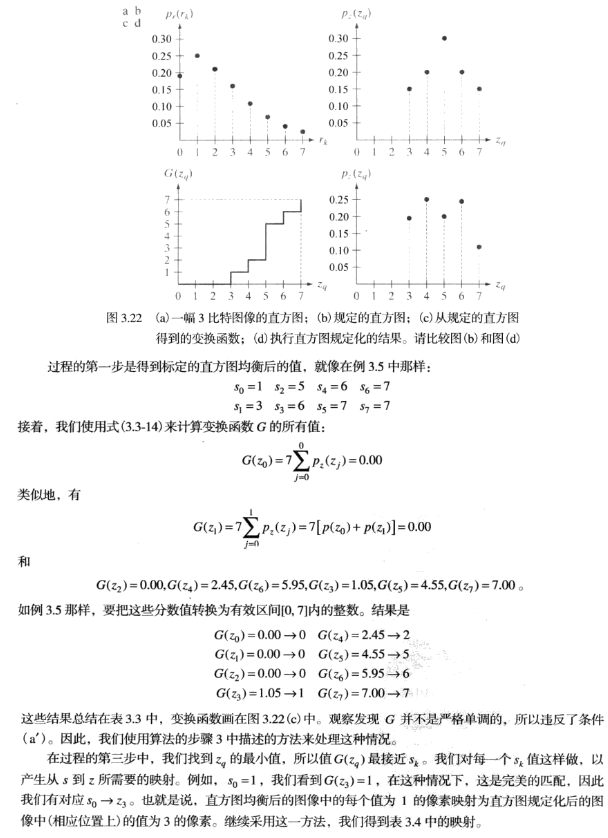
直方图规定化
直方图规定化过程

直方图规定化实例
局部直方图处理
定义:类似于卷积过程,逐像素移至另一个像素,在每个位置,计算邻域中点的直方图,不采用直方图均衡化而是规定化变换函数。
相关参量
平均灰度——所有像素的灰度值之和/ 图像中的像素总数,平均灰度的度量。
灰度方差——[f(x,y)-m]^2/图像中像素总数,图像对比度的度量。
计算实例

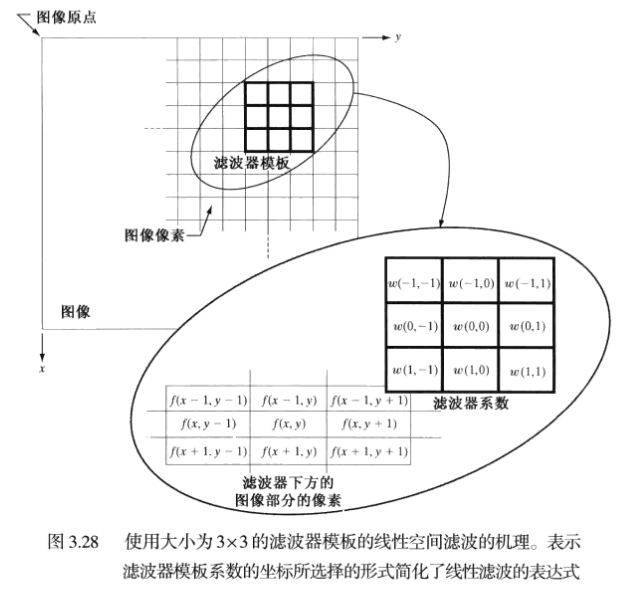
空间滤波基础
滤波过程
卷积与滤波的区别:滤波是滤波器模板移过每个位置乘积之和的处理,卷积机理类似但是滤波器首先要旋转180度。
各种滤波去噪见:https://www.cnblogs.com/E-Dreamer-Blogs/p/10458846.html
去噪定义
f(x,y)和g(x,y)分别是输入图像和锐化后的图像。如果是拉普拉斯滤波器,则常数为c = -1。如果是线性滤波器和统计排序(非线性)滤波器,则c = 1 。
非锐化掩蔽
(常用于印刷和出版界的图像锐化处理过程)
1.模糊原图像
2.从原图像中减去模糊图像(产生的差值图像称为模板)
3.将模板加到原图像上。
使用一阶微分对(非线性)图像锐化——梯度
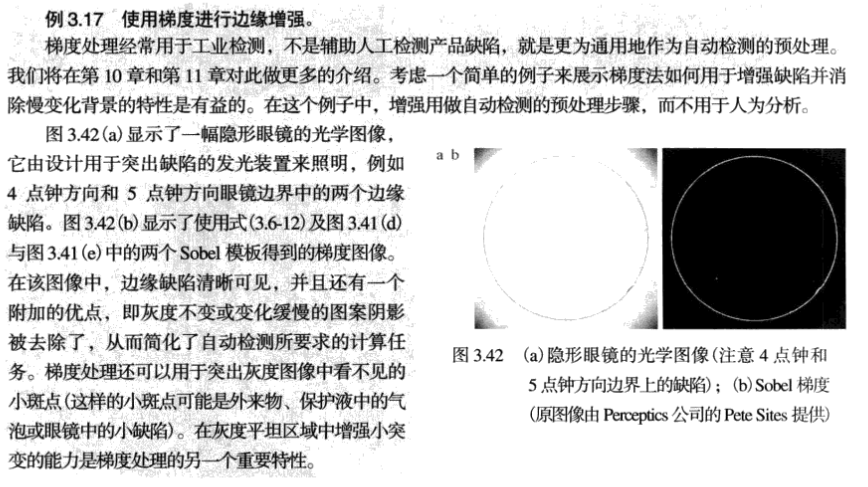
使用梯度进行边缘增强实例
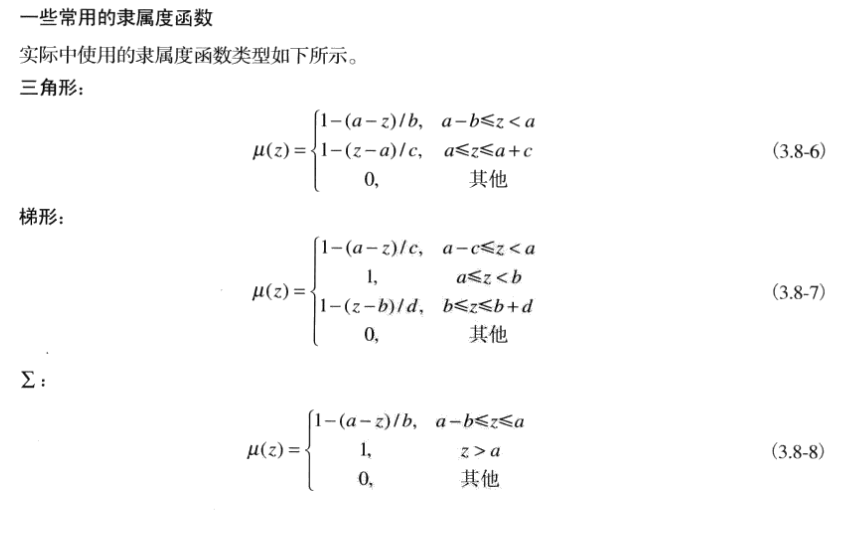
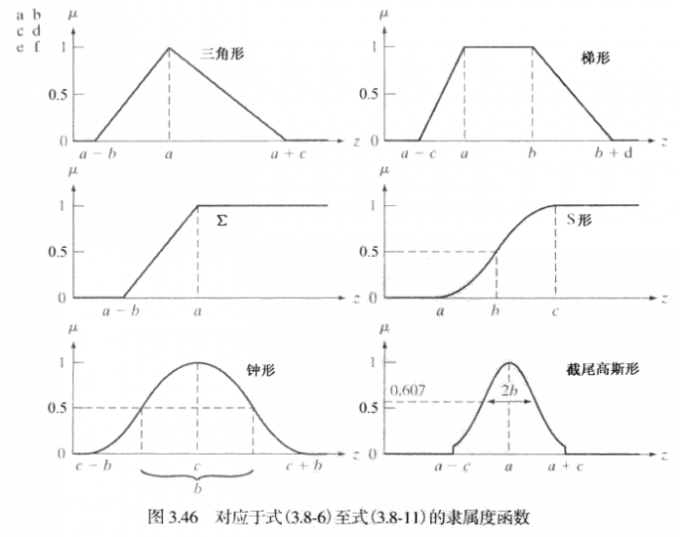
模糊集合应用
基于规则的模糊集可以用于灰度变化和空间滤波。