Linked List Cycle

一、单链表是否有环

题目描述
快慢指针：若链表有环，则两指针必在将来某一时刻相遇：

• 直观来看：本质上就是物理上的相对运动。快指针每次2步，慢指针每次1步。
  如果没有环，快指针先到达链尾，结束；
  如果有环，相对速度为1，即相当于慢指针静止，快指针每次1步，则必然在一圈之内相遇。
• 那如果快指针每次3步，4步呢？由之前的相对运动，我们知道两个指针不一定相遇。那么什么情况下可以相遇呢？
  
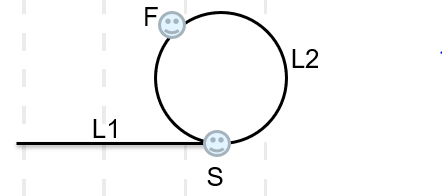
  当S第一次到达环口，F可能已经在环里转了n圈。假设S的速度为(v_s)，F的速度为(v_f)，环长为(L)，经过时间(t)相遇：

[disS=L_1, disF=L_1+L_2+nL ]

即问题转化为是否存在正整数(t)，使得S和F在环内走过的路程相等：

[v_st\%L=(L_2+nL+v_ft)\%L ]

根据模运算性质：

[(L_2+nL+(v_f-v_s)t)\%L=0 ]

再化简：

[(L_2+(v_f-v_s)t)\%L=0 ]

也就是当(L_2+(v_f-v_s)t)是环长(L)的整数倍，快慢指针可以相遇。
回头去看最简单的情形：(v_f-v_s=1)，则(t=mL-L_2)，取(m=1,t=L-L_2)。所以经过(t)步必然相遇。

// 单链表定义
struct ListNode{
    int val;
    ListNode* next;
    ListNode(int x):val(x),next(NULL) {}
};

class Solution {
public:
    bool hasCycle(ListNode* head)
    {
    	if (head == NULL)
   			return false;
  		ListNode* fast = head;
  		ListNode* slow = head;
  		while (fast && fast->next)
  		{
			fast = fast->next->next;
    		slow = slow->next;
    		if(fast == slow)
			return true;
		}
		return false;
    }
};

二、寻找环的入口

题目描述
设链头距离环的入口距离为(L_1)，相遇点距离入口距离为(L_3)，环的长度为(L)：

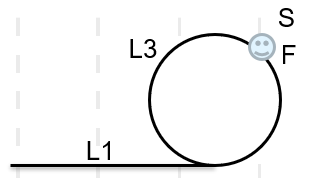
证明的本质在于求出(L_1)与(L_3)的关系。
在（一）中我们已经证明了S从入口到相遇只走了(L-L_2<L)步，即小于1圈。
由于快指针走过的路程是慢指针的2倍：

[L_1+L_2+nL+2(L-L_2)=2(L_1+L-L_2) ]

即：

[L_1=L_2+nL ]

又(L_3=L-(L-L_2)=L_2)，故有：

[L_1=nL+L_3 ]

n表示S第一次到达入口时，快指针已经绕了(n)圈。
也就是说：设两个指针(p_1, p_2)，(p_1)指向链头，(p_2)指向相遇点，每次都走一步，则两指针必在环的入口相遇。
通俗理解：(p_1)指针先走(L_3)步，此时(p_1)距离环入口还有(L_1-L_3=nL)步，同时(p_2)也走了(L_3)步，刚好到环入口。接着(p_1)继续走(nL)步，(p_2)开始绕环(n)圈，必相遇。

//单链表定义
struct ListNode{
	int val;
	ListNode* next;
	ListNode(int x):val(x),next(NULL) {}
};

class Solution{
public:
	ListNode* detectCycle(ListNode* head)
	{
		auto fast = head;
		auto slow = head;
		while(fast && fast->next)
		{
			fast = fast->next->next;
			slow = slow->next;
			if(fast == slow)
				break;
		}
		if(!fast || !fast->next)   //无环,fast走到尽头
			return nullptr;

		slow = head;   //一个指向链头,另一个指向相遇点
		while(slow != fast)
		{
			fast = fast->next;
			slow = slow->next;
		}
		return slow;    //找到入口
	}
};