Binary Search

基本型

对于一个没有重复元素的有序数组，查找某个元素。
我最常用的板子是左闭右开[l, r)：

// version 1
int biSearch(vector<int>& nums, int target) {
	int l = 0, r = nums.size();
	while (l < r) {
		int mid = l + (r - l) / 2 + 1;  // avoid dead loop
		if (target == nums[mid])
			return mid;
		if (target > nums[mid])
			l = mid;
		else
			r = mid - 1;
	}
	return -1;   // not found
}

// version 2
int biSearch(vector<int>& nums, int target) {
	int l = 0, r = nums.size();
	while (l < r) {
		int mid = l + (r - l) / 2;
		if (target == nums[mid])
			return mid;
		if (target > nums[mid])
			l = mid + 1;
		else
			r = mid;
	}
	return -1;   // not found
}

稍微扩展一些的题目有lower_bound()和upper_bound()，都是数组中有重复元素：
对于lower_bound()，即查找满足(x>=target)的最小(x)的index：

int biSearch(vector<int>& nums, int target) {
	int l = 0, r = nums.size();
	while (l < r) {
		int mid = (l + r) / 2;
		if (target > nums[mid])
			l = mid + 1;
		else
			r = mid;
	}
	return l;
}

可变形为查找最后一个小于(target)的数：即(l-1)。
对于upper_bound()，即查找满足(x>target)的最小(x)的index：

int biSearch(vector<int>& nums, int target) {
	int l = 0, r = nums.size();
	while (l < r) {
		int mid = (l + r) / 2;
		if (target >= nums[mid])
			l = mid + 1;
		else
			r = mid;
	}
	return l;
}

可变形为查找最后一个小于等于(target)的数：即(l-1)。

Rotated Sorted Array

Find the index of the target if it is in the array, else return -1. All values of the array are unique.

We can find that at least half of the elements are sorted, so we should find out whether it's on the left or the right.

Let's see an example: [0,1,2,3]{all sorted}, [3,0,1,2]{right}, [2,3,0,1]{left or right}, [1,2,3,0]{left}.
Another example: [0,1,2,3,4]{all sorted}, [4,0,1,2,3]{right}, [3,4,0,1,2]{right}, [2,3,4,0,1]{left}, [1,2,3,4,0]{left}. It is important to know that the sorted side is at least half of the array (longer). So the mid is in this side.

We can compare nums[mid] with nums[left] (or nums[right]) to decide which side is sorted. If nums[mid]>nums[left], then left half is sorted, else right is sorted.

The second step is to compare the target with nums[mid] to narrow down the range.

• Left half is sorted.
  If target>nums[mid], it must lie in the right interval. So we can make left pointer forward left = mid + 1.
  
  If target<nums[mid], there exists 2 situations:
  
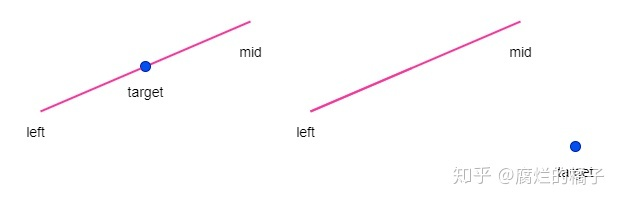
  The first graph means target is less than mid but bigger than or equal to left, we move the right pointer toward left right = mid.
  The second graph means target is less than left, thus we move the left pointer towards right left = mid + 1.

Finally if nums[mid]==nums[left], it means that left and mid are pointing to the same element due to the distinct values. In this case right must be mid or mid + 1. Where is the target? It must be on the right side of mid (actually nums[right]) or it do not exist. So we can move the left pointer by 1 to see nums[right] is equal to target or not.

• Right half is sorted.
  You can analysis this by yourself.

We can write the following code based on the previous discussion:

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        l, r = 0, len(nums) - 1
        while l <= r:
            m = l + (r - l) // 2
            if target == nums[m]:
                return m
            if nums[m] > nums[l]: # left side is sorted
                if target > nums[m]:
                    l = m + 1
                else:
                    if target >= nums[l]:
                        r = m - 1
                    else:
                        l = m + 1
            elif nums[m] < nums[l]: # right side is sorted
                if target < nums[m]:
                    r = m - 1
                else:
                    if target <= nums[r]:
                        l = m + 1
                    else:
                        r = m - 1
            else:
                l += 1
        return -1

Rotated Sorted Array II

It is the same as the last one except that the array may contains duplicates. And you do not need to find the index but return true or false.

The code is the same except that you should return T or F.

Find Minimum in Rotated Sorted Array shares the same idea:

class Solution:
    def findMin(self, nums: List[int]) -> int:
        l, r = 0, len(nums) - 1
        ans = float('inf')
        while l <= r:
            m = (l + r) >> 1
            ans = min(ans, nums[m])
            if nums[m] > nums[l]:
                ans = min(ans, nums[l])
                l = m + 1
            elif nums[m] < nums[l]:
                ans = min(ans, nums[m])
                r = m - 1
            else:
                l += 1
        return ans

Rotated Sorted Array yyds

In this case you should return the index of the target in a duplicated array. If you do not know the idea above, this will be a little harder to solve since there are many corner cases.

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        l, r = 0, len(nums) - 1
        ans = float('inf')
        while l <= r:
            m = l + (r - l) // 2
            if target == nums[m]:
                ans = min(ans, m)
                r = m - 1 # do not return since there might be smaller index
                continue
            if nums[m] > nums[l]: # left side is sorted
                if target > nums[m]:
                    l = m + 1
                else:
                    if target >= nums[l]:
                        r = m - 1
                    else:
                        l = m + 1
            elif nums[m] < nums[l]: # right side is sorted
                if target < nums[m]:
                    r = m - 1
                else:
                    if target < nums[r]:
                        l = m + 1
                    elif target > nums[r]:
                        r = m - 1
                    else:
                        if target == nums[l]:
                            ans = min(ans, l)
                            break
                        else:
                            l = m + 1
            else:
                l += 1
        return -1 if ans == float('inf') else ans