D10-树[Java数据结构和算法]

1.数组、链表和树存储方式分析

　　1.1数组的存储方式

　　（1）优点：通过下表当时访问元素，速度快。对于有序数组，还可以使用二分查找提高检索速度

　　（2）缺点：如果检索具体某个值，或者插入值（按照一定顺序）会整体移动，效率较低

　　1.2 链式存储方式的分析

　　（1）优点：在一定程度上对数组存储方式有优化（例如：插入一个数值节点，只需要将插入节点，连接到链表中即可，删除效率也很好）

　　（2）缺点：在进行检索时，效率仍然比较低，比如（检索某个值，需要从头节点开始遍历）

　　1.3 树存储方式的分析

　　能够提高数据存储，读取的效率，比如利用二叉排序树（binary Sort Tree），既可以保证数据的检索速度，同时也可以保证数据的插入，删除，修改的速度。

2.二叉树的概念和常用术语

 　　2.1 二叉树的概念

　　（1）每个节点最多只能有两个子节点的一种形式

　　（2）二叉树的子节点分为左节点和右节点

　　（3）如果该二叉树的所有叶子节点都在最后一层，并且节点总数=2^n-1，n为层数时，称为满二叉树

　　（4）如果该二叉树的所有叶子节点都在最后一层或倒数第二层，而且最后一层的叶子节点在左边连续，倒数第二层的叶子节点在右边连续，称为完全二叉树

　　2.2 二叉树的遍历

　　（1）前序遍历：先输出父节点，再遍历左子树和右子树；

　　（2）中序遍历：先遍历左子树，再输出父节点，再遍历右子树；

　　（3）后序遍历：先遍历左子树，再遍历右子树，最后输出父节点；

　　（4）分析二叉树的前序，中序，后序的遍历步骤

　　　　1）创建一颗二叉树

　　　　2) 前序遍历

　　　　　　2.1）先输出当前节点；（初始的时候事root节点）

　　　　　　2.2）如果左子节点不为空，则递归继续前序遍历；

　　　　　　2.3）如果右子节点不为空，则递归继续前序遍历

　　　　3）中序遍历

　　　　　　3.1）如果当前节点的左子节点不为空，则递归中序遍历；

　　　　　　3.2）输出当前节点；

　　　　　　3.3）如果当前节点的右子节点不为空，则递归中序遍历；

　　　　4）后序遍历

　　　　　　4.1）如果当前节点的左子节点不为空，则递归后序遍历；

　　　　　　4.2）如果当前节点的右子节点不为空，则递归后序遍历；

　　　　　　4.3）输出当前节点；

　　2.3 二叉树的前序，中序，后序的查找步骤

　　（1）前序查找

　　　　1）先判断当前节点的no是否等于要查找的；

　　　　2）如果相等，返回当前节点；

　　　　3）如果不相等，则判断当前节点的左子节点是否为空，如果不为空，则递归前序查找；

　　　　4）如果左递归前序查找，找到节点则返回，否则继续判断，当前节点的右子节点是否为空，如果不为空，则继续向右递归前序查找；

　　（2）中序查找

　　　　1）判断当前节点的左子节点是否为空，如果不为空，则递归中序查找；

　　　　2）如果找到就返回，如果没有找到就和当前节点比较，如果是则返回当前节点，否则继续进行右递归的中序查找；

　　　　3）如果右递归中序查找，找到就返回，否则就返回null；

　　（3）后序查找

　　　　1）判断当前节点的左子节点是否为空，如果不为空就继续向左后序查找；

　　　　2）如果找到就返回，没有找到就判断当前节点的右子节点是否为空，如果不为空就右递归进行后序查找，如果找到就返回；

　　　　3）就和当前节点进行比较，如果是则返回，否则返回null；

　　2.4 二叉树删除节点

　　（1）要求

　　　　1）如果删除的节点是叶子节点，则删除该节点；

　　　　2）如果删除的节点是非叶子节点，则删除该子树；

　　　　3）测试，删除掉5号叶子节点和3号子树；

　　（2）删除思路分析

　　　　1）因为二叉树是单向的，因此判断的是当前节点的子节点是否需要删除，而不是判断当前节点；

　　　　2）如果当前节点的左子节点不为空，并且左子节点就是要删除的节点，将this.left置空，并且返回，结束递归；

　　　　3）如果当前节点的右子节点不为空，并且右子节点就是要删除的节点，将this.right置空，并且返回，结束递归；

　　　　4）如果第2,3步都没有删除节点，那么向左子树递归删除；

　　　　5）如果第4步也没有删除节点，则应当向右子树递归删除；

　　　　6）考虑如果树是空树root，如果只有一个root节点，则等价于将二叉树置空。（第一步）

　　2.5 源代码

package cn.atguigu.Tree;

public class BinaryTreeDemo {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        //先创建一个二叉树
        BinaryTree binaryTree=new BinaryTree();
        //创建需要的节点
        HeroNode root=new HeroNode(1, "宋江");
        HeroNode hero2=new HeroNode(2, "吴用");
        HeroNode hero3=new HeroNode(3, "卢俊义");
        HeroNode hero4=new HeroNode(4, "林冲");
        HeroNode hero5=new HeroNode(5, "关胜");
        
        //先手动创建二叉树
        root.setLeft(hero2);
        root.setRight(hero3);
        hero3.setRight(hero4);
        hero3.setLeft(hero5);
        binaryTree.setRoot(root);
        
        //遍历测试
        /*
         * System.out.println("前序遍历"); binaryTree.preOrder();
         * System.out.println("中序遍历"); binaryTree.infixOrder();
         * System.out.println("后序遍历"); binaryTree.postOrder();
         */
        
        //查找测试
        /*
         * System.out.println("前序查找~~~~");//查找了4次 HeroNode
         * res=binaryTree.preOrderSearch(5); if(res!=null) {
         * System.out.printf("找到了，信息为no=%d,name=%s",res.getNo(),res.getName()); }else {
         * System.out.printf("没有找到no=%d 的英雄",5); } System.out.println();
         * System.out.println("中序查找~~~~");//查找了3次 res=binaryTree.infixOrderSearch(5);
         * if(res!=null) {
         * System.out.printf("找到了，信息为no=%d,name=%s",res.getNo(),res.getName()); }else {
         * System.out.printf("没有找到no=%d 的英雄",5); } System.out.println();
         * System.out.println("后序查找~~~~");//查找了2次 res=binaryTree.postOrderSearch(5);
         * if(res!=null) {
         * System.out.printf("找到了，信息为no=%d,name=%s",res.getNo(),res.getName()); }else {
         * System.out.printf("没有找到no=%d 的英雄",5); }
         */
        
        //删除测试
        System.out.println("删除前前序遍历~~~~");
        binaryTree.preOrder();//1,2,3,5,4
//        binaryTree.delNode(5);
        binaryTree.delNode(3);
        System.out.println("删除后前序遍历~~~~");
        binaryTree.preOrder();//1,2,3,4
    }

}
//定义BinaryTree 二叉树
class BinaryTree{
    private HeroNode root;

    public void setRoot(HeroNode root) {
        this.root = root;
    }
    //删除节点
    public void delNode(int no) {
        if(root!=null) {
            //单独对root节点进行判断
            if(root.getNo()==no) {
                root=null;
            }else {
                root.delNode(no);
            }
        }else {
            System.out.println("空树，不能删除");
        }
    }
    
    //前序遍历
    public void preOrder() {
        if(this.root!=null) {
            this.root.preOrder();
        }else {
            System.out.println("当前二叉树为空，无法遍历");
        }
    }
    
    //中序遍历
    public void infixOrder() {
        if(this.root!=null) {
            this.root.infixOrder();
        }else {
            System.out.println("当前二叉树为空，无法遍历");
        }    
    }
    //后序遍历
    public void postOrder() {
        if(this.root!=null) {
            this.root.postOrder();
        }else {
            System.out.println("当前二叉树为空，无法遍历");
        }    
    }
    
    //前序查找
    public HeroNode preOrderSearch(int no) {
        if(root!=null) {
            return root.preOrderSearch(no);
        }else {
            return null;
        }
    }
    
    //中序查找
    public HeroNode infixOrderSearch(int no) {
        if(root!=null) {
            return root.infixOrderSearch(no);
        }else {
            return null;
        }
    }
    //后序查找
    public HeroNode postOrderSearch(int no) {
        if(root!=null) {
            return root.postOrderSearch(no);
        }else {
            return null;
        }
    }
}


//先创建HeroNode节点
class HeroNode{
    private int no;
    private String name;
    private HeroNode left;//默认null
    private HeroNode right;//默认null
    public HeroNode(int no, String name) {
        this.no = no;
        this.name = name;
    }
    public int getNo() {
        return no;
    }
    public void setNo(int no) {
        this.no = no;
    }
    public String getName() {
        return name;
    }
    public void setName(String name) {
        this.name = name;
    }
    public HeroNode getLeft() {
        return left;
    }
    public void setLeft(HeroNode left) {
        this.left = left;
    }
    public HeroNode getRight() {
        return right;
    }
    public void setRight(HeroNode right) {
        this.right = right;
    }
    @Override
    public String toString() {
        return "HeroNode [no=" + no + ", name=" + name + "]";
    }
    //递归删除节点
    public void delNode(int no) {
        if(this.left!=null&&this.left.no==no) {//如果当前节点的左子节点不为空，并且左子节点就是要删除的节点，将this.left置空，并且返回，结束递归；
            this.left=null;
            return;
        }
        if(this.right!=null&&this.right.no==no) {//如果当前节点的右子节点不为空，并且右子节点就是要删除的节点，将this.right置空，并且返回，结束递归；
            this.right=null;
            return;
        }
        if(this.left!=null) {//向左子树递归删除
            this.left.delNode(no);            
        }
        if(this.right!=null) {//向右子树递归删除
            this.right.delNode(no);
        }
    }
    
    
    //编写前序遍历的方法
    public void preOrder() {
        System.out.println(this);//先输出父节点
        //递归向左子树遍历
        if(this.left!=null) {
            this.left.preOrder();
        }
        //递归向右子树遍历
        if(this.right!=null) {
            this.right.preOrder();
        }
    }
    //中序遍历
    public void infixOrder() {
        //向左子树遍历
        if(this.left!=null) {
            this.left.infixOrder();
        }
        //输出当前节点
        System.out.println(this);
        //向右子树遍历
        if(this.right!=null) {
            this.right.infixOrder();
        }
    }
    //后序遍历
    public void postOrder() {
        //向左子树遍历
        if(this.left!=null) {
            this.left.postOrder();
        }
        //向右子树遍历
        if(this.right!=null) {
            this.right.postOrder();
        }
        //输出当前节点
        System.out.println(this);
    }
    
    //前序查找
    /**
     * 
     * @param no 查找no
     * @return 如果找到就返回该Node，否则返回null
     */
    public HeroNode preOrderSearch(int no) {
        System.out.println("进入前序查找");
        //比较当前节点是否是
        if(this.no==no) {
            return this;
        }
        //向左判断
        HeroNode resNode=null;
        if(this.left!=null) {
            resNode=this.left.preOrderSearch(no);
        }
        if(resNode!=null) {
            return resNode;
        }
        //向右判断
        if(this.right!=null) {
            resNode=this.right.preOrderSearch(no);
        }
        return resNode;
    }
    
    //中序遍历查找
    public HeroNode infixOrderSearch(int no) {
        //向左判断
        HeroNode resNode=null;
        if(this.left!=null) {
            resNode=this.left.infixOrderSearch(no);
        }
        if(resNode!=null) {
            return resNode;
        }
        System.out.println("进入中序查找");
        //判断当前节点
        if(this.no==no) {
            return this;
        }
        //向右判断
        if(this.right!=null) {
            resNode=this.right.infixOrderSearch(no);
        }
        return resNode;
    }
    
    //后序遍历查找
    public HeroNode postOrderSearch(int no) {
        //向左判断
        HeroNode resNode=null;
        if(this.left!=null) {
            resNode=this.left.postOrderSearch(no);
        }
        if(resNode!=null) {
            return resNode;
        }
        //向右判断
        if(this.right!=null) {
            resNode=this.right.postOrderSearch(no);
        }
        if(resNode!=null) {
            return resNode;
        }
        //判断当前节点
        System.out.println("进入后序查找");
        if(this.no==no) {
            return this;
        }else {
            return null;
        }
    }
}

3.顺序存储二叉树

　　3.1顺序存储二叉树的特点

　　（1）顺序二叉树通常只考虑完全二叉树

　　（2）第n个元素的左节点为2*n+1

　　（3）第n个元素的右节点为2*n+2

　　（4）第n个元素的父节点为(n-1)/2

　　（5）n表示二叉树中第几个元素（从0开始编号）

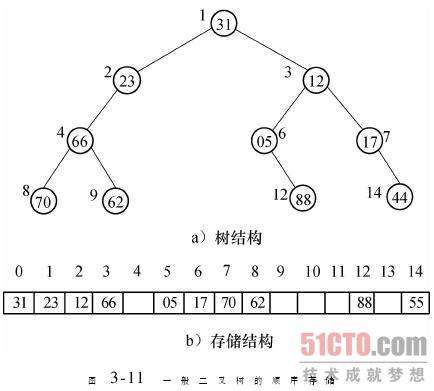
　　3.2 需求:数组{1,2,3,4,5,6,7}，要求以二叉树前序遍历的方式进行遍历，结果应当为{1,2,4,5,3,6,7}

package cn.atguigu.Tree;

public class ArrBinaryTreeDemo {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] arr= {1,2,3,4,5,6,7};
        ArrBinaryTree arrbinaryTree=new ArrBinaryTree(arr);
        arrbinaryTree.preOrder();
    }

}
//编写ArrBinaryTree，实现顺序存储二叉树遍历
class ArrBinaryTree{
    private int[] arr;//存储数据节点的数组

    public ArrBinaryTree(int[] arr) {
        this.arr = arr;
    }
    //重载
    public void preOrder() {
        this.preOrder(0);
    }
    
    //编写一个方法，完成顺序存储二叉树的前序遍历
    /**
     * 
     * @param index 表示数组的下标 
     */
    public void preOrder(int index) {
        //如果数组为空，或者arr.length=0
        if(arr==null||arr.length==0) {
            System.out.println("数组为空，不能按照二叉树的前序遍历");
        }
        //输出当前这个元素
        System.out.println(arr[index]);
        //向左
        if((index*2+1)<arr.length) {
            preOrder(2*index+1);
        }
        //向右
        if((index*2+2)<arr.length) {
            preOrder(2*index+2);
        }
    }
}

 　　3.3 顺序二叉树的实际应用场景是堆排序

4. 线索二叉树

　　4.1 基本介绍

　　（1）n个节点的二叉链表中含有n+1个空指针域，利用二叉链表中的空指针域，存放指向该节点在某种遍历次序下的前驱和后继节点的指针

　　（2）这种添加了线索的二叉链表称为线索链表，相应的二叉树为线索二叉树(Threaded BinaryTree)。根据线索性质的不同，线索二叉树可分为前序线索二叉树，中序线索二叉树，后序线索二叉树三种；

　　（3）一个节点的前一个节点，称为前驱节点；

　　（4）一个节点的后一个节点，称为后继节点；

　　4.2 线索二叉树应用案例

　　（1）当线索化二叉树后，Node节点的属性left和right，有以下两种情况：left指向的是左子树，也可能指向的是前驱节点；right指向的是右子树，也可能指向后继节点；

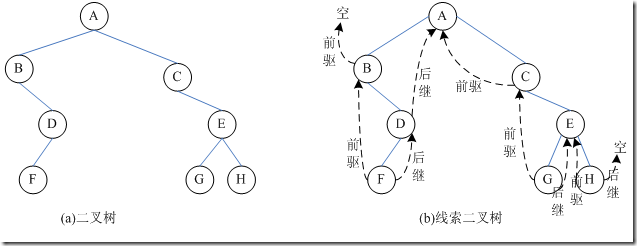　　　　中序遍历的结果：{B,F,D,A,C,G,E,H}

　　（2）源代码

package cn.atguigu.Tree;

public class ThreadedBinaryTreeDemo {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        //中序线索二叉树测试
        ThreadedHeroNode root=new ThreadedHeroNode(1,"tom");
        ThreadedHeroNode node2=new ThreadedHeroNode(3,"jack");
        ThreadedHeroNode node3=new ThreadedHeroNode(6,"smith");
        ThreadedHeroNode node4=new ThreadedHeroNode(8,"mary");
        ThreadedHeroNode node5=new ThreadedHeroNode(10,"king");
        ThreadedHeroNode node6=new ThreadedHeroNode(14,"dim");
        
        //手动创建二叉树
        root.setLeft(node2);
        root.setRight(node3);
        node2.setLeft(node4);
        node2.setRight(node5);
        node3.setLeft(node6);
        
        //测试线索化
        ThreadedBinaryTree tree=new ThreadedBinaryTree();
        tree.setRoot(root);
        tree.threadedNodes();//线索化
        
        //测试,以10节点测试
        ThreadedHeroNode left=node5.getLeft();
        System.out.println("10号节点的前驱节点是："+left);
        
        //使用线索化遍历的方式
        System.out.println("使用线索化的方式遍历，线索化二叉树");
        tree.threadedList();
    }

}
//定义ThreadedBinaryTree 二叉树 实现了线索化功能的二叉树
class ThreadedBinaryTree{
    private ThreadedHeroNode root;
    //为了实现线索化，需要创建要给指向当前节点的新节点的指针
    private ThreadedHeroNode pre=null;
    //在递归进行线索化时，pre总是保留前一个节点
    
    public void setRoot(ThreadedHeroNode root) {
        this.root = root;
    }
    
    //重载
    public void threadedNodes() {
        this.threadedNodes(root);
    }
    //遍历线索化二叉树的方法
    public void threadedList() {
        //定义一个遍历，存储当前遍历的节点，从root开始
        ThreadedHeroNode node=root;
        while(node!=null) {
            //循环的找到leftType=1的节点
            //后面随着遍历而变化，因为当leftType=1时，说明该节点是按照线索化
            //处理后的有效节点
            while(node.getLeftType()==0) {
                node=node.getLeft();
            }
            //输出当前节点
            System.out.println(node);
            //如果当前节点的右指针指向的是后继节点，就一直输出
            while(node.getRightType()==1) {
                node=node.getRight();
                System.out.println(node);
            }
            //替换遍历节点
            node=node.getRight();
        }
    }
    
    //编写对二叉树进行中序线索化的方法
    /**
     * 
     * @param node 当前需要线索化的节点
     */
    public void threadedNodes(ThreadedHeroNode node) {
        //如果node==null，不能线索化
        if(node==null) {
            return;
        }
        //先线索化左子树
        threadedNodes(node.getLeft());
        //线索化当前节点
        //处理当前节点的前驱节点
        if(node.getLeft()==null) {
            //让当前节点的做指针指向当前节点
            node.setLeft(pre);
            node.setLeftType(1);//修改当前节点的指针类型，当前节点指向前驱节点
        }
        //处理后继节点
        if(pre!=null&&pre.getRight()==null) {
            pre.setRight(node);//让前驱节点的右指针指向当前指针
            pre.setRightType(1);//修改前驱节点的指针类型
        }
        //每处理一个节点后，让当前节点是下一个节点的前驱节点 
        pre=node;
        
        //后线索化右子树
        threadedNodes(node.getRight());
    }
}



//先创建ThreadedHeroNode节点
class ThreadedHeroNode{
    private int no;
    private String name;
    private ThreadedHeroNode left;//默认null
    private ThreadedHeroNode right;//默认null
    //说明
    //1.如果leftType==0表明指向左子树，1表示指向前驱节点
    //2如果righttype==0表明指向右子树，1表示指向后继节点
    private int leftType;
    private int rightType;
    
    public int getLeftType() {
        return leftType;
    }
    public void setLeftType(int leftType) {
        this.leftType = leftType;
    }
    public int getRightType() {
        return rightType;
    }
    public void setRightType(int rightType) {
        this.rightType = rightType;
    }
    public ThreadedHeroNode(int no, String name) {
        this.no = no;
        this.name = name;
    }
    public int getNo() {
        return no;
    }
    public void setNo(int no) {
        this.no = no;
    }
    public String getName() {
        return name;
    }
    public void setName(String name) {
        this.name = name;
    }
    public ThreadedHeroNode getLeft() {
        return left;
    }
    public void setLeft(ThreadedHeroNode left) {
        this.left = left;
    }
    public ThreadedHeroNode getRight() {
        return right;
    }
    public void setRight(ThreadedHeroNode right) {
        this.right = right;
    }
    @Override
    public String toString() {
        return "ThreadedHeroNode [no=" + no + ", name=" + name + "]";
    }
}