2020 Multi-University Training Contest 2 In Search of Gold
题目大意:
给你一颗大小是n的树,每一条边都有两个值一个a一个b,选择k条a边,n-1-k 条b边,问这棵树的直径最短是多少?
题解:
很自然的定义 (dp[i][j]) 表示对于子树 (i) ,有 (j) 条边来自 a 的最远距离的最小值。
那么转移方程就是
(dp[u][j]=min(dp[u][j],max(dp[v][x]+a,dp[u][j-x-1]),max(dp[v][x]+b,dp[u][j-x])))
这个转移方程表示的是,如果从子节点v转移,那么有两种选择,一种就是这个子节点要这个条a边,一个是这个子节点不要这条a边的转移。
但是呢,这样转移会出现一个问题。
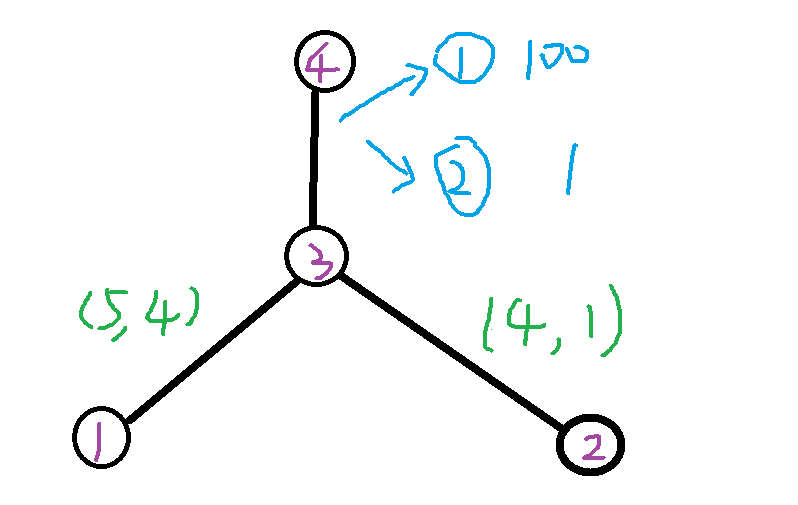
对于这棵树,假设k=1,括号左边表示a,右边表示b,到3这个点有两种可能选择(如果选了一条a边) (5,1) (4,4)
所有按照上面的转移方程3这个点如果选一条a边的结果是 (4,4) 。
这样的话,那么上面3到4这条边是 (1000,1) 那么直径是不是 4+4=8,那么没有下面选择 (5,1) 直径是 5+1 更优,如果下面选择 (5,1) ,那么3到4这条边是(1000,100) 那么也会出现问题。
所以如果直接这样转移肯定会出问题的,那怎么转移是对的呢?
先思考一下为什么这个会影响结果?其实就是因为子树可能成为直径,如果保证子树直径小于等于整棵树的直径,那么是不是就没什么影响了,但是怎么判断子树的直径有没有大于整棵树的直径呢?这个可以二分求解,所以二分一下这个直径长度,如果这个长度子节点合并的时候大于这个直径长度,那么就不从这里转移即可,不从这里转移表示不要这个状态。
最后怎么判断这个check是否为真?这个很好判断,因为 (dp[i][j]) 的转移必须要求以 (i) 为根节点的树的直径都小于等于这个mid。
最后说一下这个复杂度其实只有 (O(n*k*log)) 为什么不是 (O(n*k*k*log)) ,推荐博客:https://blog.csdn.net/lyd_7_29/article/details/79854245
#include <bits/stdc++.h>
#define inf 0x3f3f3f3f
#define inf64 0x3f3f3f3f3f3f3f3f
using namespace std;
typedef long long ll;
const int maxn = 2e4+10;
int head[maxn],nxt[maxn<<1],to[maxn<<1],cnt,a[maxn<<1],b[maxn<<1];
void add(int u,int v,int x,int y){
++cnt,to[cnt]=v,nxt[cnt]=head[u],a[cnt]=x,b[cnt]=y,head[u]=cnt;
++cnt,to[cnt]=u,nxt[cnt]=head[v],a[cnt]=x,b[cnt]=y,head[v]=cnt;
}
ll dp[maxn][22];
//dp[i][j] 表示已i为根节点的子树,选择了j条a边,最远距离最小。
int n,k;
int siz[maxn];
ll tmp[22];
//tmp[i] 表示选了i条a边的最远距离
void dfs(int u,int pre,ll x){
siz[u]=0;
memset(dp[u],0,sizeof(dp[u]));
for(int i=head[u];i;i=nxt[i]){
int v = to[i];
if(v == pre) continue;
dfs(v,u,x);
int num = min(k,siz[u]+siz[v]+1);
for(int j=0;j<=num;j++) tmp[j]=x+1;
for(int j=0;j<=siz[u];j++){
for(int h=0;h<=siz[v]&&h+j<=k;h++){
if(dp[u][j]+dp[v][h]+a[i]<=x){
tmp[j+h+1]=min(tmp[j+h+1],max(dp[u][j],dp[v][h]+a[i]));
}
if(dp[u][j]+dp[v][h]+b[i]<=x){
tmp[j+h]=min(tmp[j+h],max(dp[u][j],dp[v][h]+b[i]));
}
}
}
siz[u]=num;
for(int j=0;j<=siz[u];j++) dp[u][j]=tmp[j];
}
}
bool check(ll x){
dfs(1,0,x);
if(dp[1][k]<=x) return true;
return false;
}
void init(int n){
cnt=0;
for(int i=0;i<=n;i++) head[i]=0;
}
int main(){
int t;
scanf("%d",&t);
while(t--){
scanf("%d%d",&n,&k);
init(n);
for(int i=1;i<n;i++){
int u,v,x,y;
scanf("%d%d%d%d",&u,&v,&x,&y);
add(u,v,x,y);
}
ll l=1,r=inf64,ans=0;
while(l<=r){
ll mid=(l+r)>>1ll;
if(check(mid)) ans=mid,r=mid-1;
else l=mid+1;
}
printf("%lld
",ans);
}
}