【例9.5】城市交通路网
链接:http://ybt.ssoier.cn:8088/problem_show.php?pid=1261
时间限制: 1000 ms 内存限制: 65536 KB
【题目描述】
下图表示城市之间的交通路网,线段上的数字表示费用,单向通行由A->E。试用动态规划的最优化原理求出A->E的最省费用。
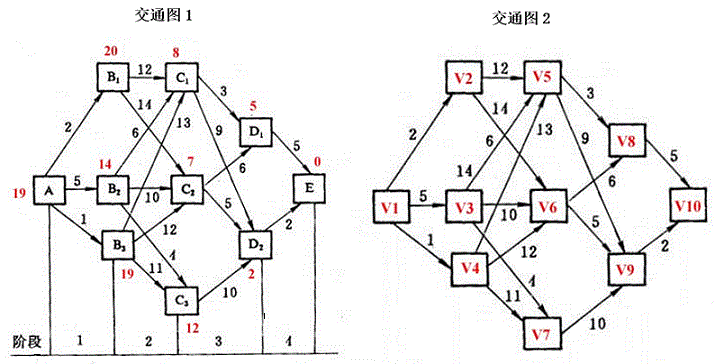
如图:求v1到v10的最短路径长度及最短路径。
【输入】
第一行为城市的数量N;
后面是N*N的表示两个城市间费用组成的矩阵。
【输出】
A->E的最省费用。
【输入样例】
10 0 2 5 1 0 0 0 0 0 0 0 0 0 0 12 14 0 0 0 0 0 0 0 0 6 10 4 0 0 0 0 0 0 0 13 12 11 0 0 0 0 0 0 0 0 0 0 3 9 0 0 0 0 0 0 0 0 6 5 0 0 0 0 0 0 0 0 0 10 0 0 0 0 0 0 0 0 0 0 5 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0
【输出样例】
minlong=19 1 3 5 8 10
题解:f[i]表示第i个城市到终点的最短距离
#include<iostream> #include<cstdio> #include<cstring> using namespace std; int mp[105][105],f[105],a[105]; const int maxn=10000005; int main() { int n; cin>>n; for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) cin>>mp[i][j]; for(int i=1;i<=n;i++)f[i]=maxn; f[n]=0;a[n]=0; for(int i=n-1;i>0;i--) for(int j=i+1;j<=n;j++) if(mp[i][j]&&mp[i][j]+f[j]<f[i]) { f[i]=mp[i][j]+f[j]; a[i]=j; } cout<<"minlong="<<f[1]<<endl; int k=1; printf("1"); while(k) { if(k!=1)printf(" %d",k); k=a[k]; } }