Noip2016day2

zoukankan html css js c++ java

Noip2016day2
P2822 组合数问题

题目描述

组合数 $C_n^mCnm 表示的是从 nn 个物品中选出 mm 个物品的方案数。举个例子，从 (1,2,3)(1,2,3) 三个物品中选择两个物品可以有 (1,2),(1,3),(2,3)(1,2),(1,3),(2,3) 这三种选择方法。根据组合数的定义，我们可以给出计算组合数 C_n^mCnm 的一般公式：$

$C_n^m=frac{n!}{m!(n-m)!}Cnm=m!(n−m)!n!$

其中

小葱想知道如果给定 $C_i^jCij 是 kk 的倍数。$

输入输出格式

输入格式：

第一行有两个整数

接下来

输出格式：

共 $C_i^jCij 是 kk 的倍数。$

输入输出样例
输入样例#1：复制
1 2 3 3

输出样例#1：复制
1
输入样例#2：复制
2 5 4 5 6 7

输出样例#2：复制
0 7
说明

【样例1说明】

在所有可能的情况中，只有 $C_2^1 = 2C21=2 是2的倍数。$

【子任务】

题解：杨辉三角求组合数，中间几组数据忽略了M<N就ＷＡ了，没预处理；求和在线的二维树状数组，可以先dp预处理更优；
#include <bits/stdc++.h> #define ll long long using namespace std; int n,m,k,t,N; int k1, k2; const int M = 2010; ll c1[M][M],c2[M][M],a1[M][M],a2[M][M]; void add(int x, int y, int k){ x++,y++; if(k == 1){ for( ; x <= N; x += x&(-x)) for(int j = y ; j <= N; j += j&(-j)) a1[x][j]++; } if(k == 2){ for( ; x <= N; x += x&(-x)) for(int j = y ; j <= N; j += j&(-j)) a2[x][j]++; } } ll sum(int x, int y, int k){ ll ans = 0; x++,y++; if(k == k1){ for( ; x > 0; x -= x&(-x)) for(int j = y ; j > 0; j -= j&(-j)) ans += a1[x][j]; } if(k == k2){ for( ; x > 0; x -= x&(-x)) for(int j = y ; j > 0; j -= j&(-j)) ans += a2[x][j]; } return ans; } void init(int a, int b, int n){ k1 = a, k2 = b, N = n; c1[0][0] = c2[0][0] = 1; for(int i = 1; i <= n; i++) for(int j = 0; j <= i; j++){ if(!j)c1[i][j] = c2[i][j] = 1; else c1[i][j] = (c1[i - 1][j-1] + c1[i - 1][j]) % k1, c2[i][j] = (c2[i - 1][j-1] + c2[i - 1][j]) % k2; if(!c1[i][j])add(i, j, 1); if(!c2[i][j])add(i, j, 2); } } int main() { // freopen("problem.in","r",stdin); // freopen("problem.out","w",stdout); scanf("%d%d",&t,&k); switch(k){ case 2: case 3: init(2, 3, 5);break; case 4: case 5: init(4, 5, 10);break; case 6: case 7: init(6, 7, 12);break; case 8: case 9: init(8, 9, 105);break; case 10: case 11: init(10, 11, 2005);break; case 12: case 13: init(12, 13, 75);break; case 14: case 15: init(14, 15, 105);break; case 16: case 17: init(16, 17, 105);break; case 18: case 19: init(18, 19, 2005);break; case 20: case 21: init(20, 21, 2005);break; } while(t--){ scanf("%d%d",&n,&m); printf("%lld ",sum(n, m, k)); } return 0; }

View Code
P2827 蚯蚓

题目描述

本题中，我们将用符号

蛐蛐国最近蚯蚓成灾了！隔壁跳蚤国的跳蚤也拿蚯蚓们没办法，蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。

蛐蛐国里现在共有 $a_iai ( i=1,2,dots,ni=1,2,…,n)，并保证所有的长度都是非负整数（即：可能存在长度为 00 的蚯蚓）。$

每一秒，神刀手会在所有的蚯蚓中，准确地找到最长的那一只（如有多个则任选一个）将其切成两半。神刀手切开蚯蚓的位置由常数

蛐蛐国王知道这样不是长久之计，因为蚯蚓不仅会越来越多，还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物，但是救兵还需要

蛐蛐国王希望知道这
蛐蛐国王当然知道怎么做啦！但是他想考考你……

输入输出格式

输入格式：

第一行包含六个整数

第二行包含 $a_1, a_2, dots, a_na1,a2,…,an ，即初始时 nn 只蚯蚓的长度。$

同一行中相邻的两个数之间，恰好用一个空格隔开。

保证 $10^51≤n≤105 ， 0 leq m leq 7 imes 10^60≤m≤7×106 ， 0 < u < v leq 10^90<u<v≤109 ， 0 leq q leq 2000≤q≤200 ， 1 leq t leq 711≤t≤71 ， 0 leq a_i leq 10^80≤ai≤108 。$

输出格式：

第一行输出 $left lfloor frac{m}{t} ight floor$

第二行输出 $left lfloor frac{n+m}{t} ight floor$

同一行中相邻的两个数之间，恰好用一个空格隔开。即使某一行没有任何数需要输出，你也应输出一个空行。

请阅读样例来更好地理解这个格式。

输入输出样例
输入样例#1：复制
3 7 1 1 3 1 3 3 2

输出样例#1：复制
3 4 4 4 5 5 6 6 6 6 5 5 4 4 3 2 2
输入样例#2：复制
3 7 1 1 3 2 3 3 2

输出样例#2：复制
4 4 5 6 5 4 3 2
输入样例#3：复制
3 7 1 1 3 9 3 3 2

输出样例#3：复制
//空行 2
说明

【样例解释1】

在神刀手到来前：3只蚯蚓的长度为3,3,2。

1秒后：一只长度为3的蚯蚓被切成了两只长度分别为1和2的蚯蚓，其余蚯蚓的长度增加了1。最终4只蚯蚓的长度分别为(1,2),4,3。括号表示这个位置刚刚有一只蚯蚓被切断

2秒后：一只长度为4的蚯蚓被切成了1和3。5只蚯蚓的长度分别为：2,3,(1,3),4。

3秒后：一只长度为4的蚯蚓被切断。6只蚯蚓的长度分别为：3,4,2,4,(1,3)。

4秒后：一只长度为4的蚯蚓被切断。7只蚯蚓的长度分别为：4,(1,3),3,5,2,4。

5秒后：一只长度为5的蚯蚓被切断。8只蚯蚓的长度分别为：5,2,4,4,(1,4),3,5。

6秒后：一只长度为5的蚯蚓被切断。9只蚯蚓的长度分别为：（1,4),3,5,5,2,5,4,6。

7秒后：一只长度为6的蚯蚓被切断。10只蚯蚓的长度分别为：2,5,4,6,6,3,6,5,(2,4)。所以，7秒内被切断的蚯蚓的长度依次为3,4,4,4,5,5,6。7秒后，所有蚯蚓长度从大到小排序为6,6,6,5,5,4,4,3,2,2

【样例解释2】

这个数据中只有t=2与上个数据不同。只需在每行都改为每两个数输出一个数即可。

虽然第一行最后有一个6没有被输出，但是第二行仍然要重新从第二个数再开始输出。

【样例解释3】

这个数据中只有t=9与上个数据不同。

注意第一行没有数要输出，但也要输出一个空行。

【数据范围】

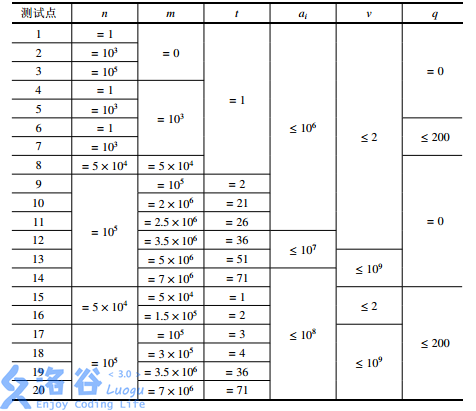
题解：开三个队列，1存原来的，2存第一段，3存第二段，每次找3个队列中最大的，可以保证队列是单调递减的，证明如下：

if La > Lb, 经过m秒后， La1 = p * La + m*q, La2 = （1-P）* L a + m* q;

　　　　　此时砍B ， Lb1 = p*(Lb +m*q), Lb2 = (1-p) * (Lb + m*q); ( p < 1)

　　　　　　　　La1 > Lb1 , La2 > Lb2;

这道题卡常，最后合并3个队列时直接找，不要再开一个数组
#include <bits/stdc++.h> using namespace std; #define ll long long ll w[4][8000005], a[8000005]; int h[4],tt[4]; const ll inf = 1e15; bool cmp(ll a, ll b){return a>b;} void read(ll &x){ ll f=1;x=0;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();} while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();} x*=f; } int main() { //freopen("earthworm.in","r",stdin); //freopen("earthworm.out","w",stdout); double p = 0; int cnt = 0, n, m, q, u, v, t; scanf("%d%d%d%d%d%d",&n,&m,&q,&u,&v,&t); p = u*1.0 / v; for(int i = 1; i <= n; i++)read(w[1][i]); sort(w[1]+1,w[1]+1+n,cmp); h[1] = h[2] = h[3] = 1; tt[1] = n; tt[2] = tt[3] = 0; int tot = n; for(int i = 1; i <= m; i++){ ll b, c, mx = -inf; tot++; int mh; for(int j = 1; j <= 3; j++) if(w[j][h[j]] > mx && h[j] <= tt[j]) mx = w[j][h[j]], mh = j; h[mh]++; //printf("%I64d %d ",mx+cnt,mh); mx += cnt; if(i % t == 0)printf("%lld ",mx); b = floor(p*mx); c = mx- b; cnt += q; w[2][++tt[2]] = b-cnt; w[3][++tt[3]] = c-cnt; } printf(" "); int qq = 0; for(int i = 1; i <= tot; i++){ ll mx = -inf; int mh; for(int j = 1; j <= 3; j++) if(w[j][h[j]] > mx && h[j] <= tt[j]) mx = w[j][h[j]], mh = j; h[mh]++; if(i%t == 0)printf("%lld ",mx+cnt); } return 0; }

View Code
P2831 愤怒的小鸟

题目描述

Kiana 最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于 $y=ax^2+bxy=ax2+bx 的曲线，其中 a,ba,b 是 Kiana 指定的参数，且必须满足 a < 0a<0 ， a,ba,b 都是实数。$

当小鸟落回地面（即

在游戏的某个关卡里，平面的第一象限中有 $left(x_i,y_i ight)(xi,yi) 。$

如果某只小鸟的飞行轨迹经过了 $x_i, y_i ight)(xi,yi) ，那么第 ii 只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；$

如果一只小鸟的飞行轨迹没有经过 $x_i, y_i ight)(xi,yi) ，那么这只小鸟飞行的全过程就不会对第 ii 只小猪产生任何影响。$

例如，若两只小猪分别位于 $y=-x^2+4xy=−x2+4x 的小鸟，这样两只小猪就会被这只小鸟一起消灭。$

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对 Kiana 来说都很难，所以 Kiana 还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。

假设这款游戏一共有

输入输出格式

输入格式：

第一行包含一个正整数

下面依次输入这 $x_i,y_ixi,yi ，表示第 ii 只小猪坐标为 (x_i,y_i)(xi,yi) 。数据保证同一个关卡中不存在两只坐标完全相同的小猪。$

如果

如果

如果

保证 $x_i,y_i < 100<xi,yi<10 ，输入中的实数均保留到小数点后两位。$

上文中，符号

输出格式：

对每个关卡依次输出一行答案。

输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量。

输入输出样例
输入样例#1：复制
2 2 0 1.00 3.00 3.00 3.00 5 2 1.00 5.00 2.00 8.00 3.00 9.00 4.00 8.00 5.00 5.00

输出样例#1：复制
1 1
输入样例#2：复制
3 2 0 1.41 2.00 1.73 3.00 3 0 1.11 1.41 2.34 1.79 2.98 1.49 5 0 2.72 2.72 2.72 3.14 3.14 2.72 3.14 3.14 5.00 5.00

输出样例#2：复制
2 2 3
输入样例#3：复制
1 10 0 7.16 6.28 2.02 0.38 8.33 7.78 7.68 2.09 7.46 7.86 5.77 7.44 8.24 6.72 4.42 5.11 5.42 7.79 8.15 4.99

输出样例#3：复制
6
说明

【样例解释1】

这组数据中一共有两个关卡。

第一个关卡与【问题描述】中的情形相同，2只小猪分别位于（1.00,3.00)和 (3.00,3.00)，只需发射一只飞行轨迹为y = -x^2 + 4x的小鸟即可消灭它们。

第二个关卡中有5只小猪，但经过观察我们可以发现它们的坐标都在抛物线 y = -x^2 + 6x上，故Kiana只需要发射一只小鸟即可消灭所有小猪。

【数据范围】

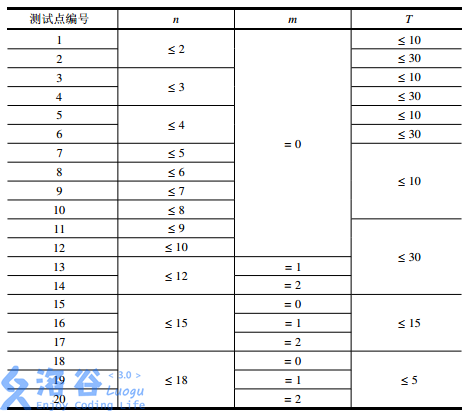
题解：原题还写错了，应该反思；

每只猪有打和不打两个状态，所以状压dp；

O(N*N*2^N) + O(N*N*N) 预处理

dp[s | g[i][j] ] = min(dp[s] +1), dp[0] = 0;

dp[s] 表示s状态需要多少只鸟， g[i][j] 是预处理的鸟的抛物线可以打那些猪；处理g[i][j]时没用的边踢掉，不然会T；
#include <bits/stdc++.h> using namespace std; const int M = 20; double x[M], y[M], a[M][M], b[M][M]; int g[M][M], dp[1<<20]; const double eps = 1e-6; bool build(int i, int j){ a[i][j] = (y[i]/x[i] - y[j]/x[j]) / (x[i] - x[j]); if(a[i][j] >= 0)return false; b[i][j] = (y[i] - a[i][j]*x[i]*x[i]) / x[i]; return 1; } bool check(int i, int j, int k){ double tmp = a[i][j]*x[k]*x[k] + b[i][j] * x[k]; if(fabs(tmp - y[k]) < eps) return 1; return 0; } int main() { //freopen("angrybirds.in","r",stdin); //freopen("angrybirds.out","w",stdout); int T, n, m; scanf("%d",&T); while(T--){ scanf("%d%d",&n,&m); for(int i = 1; i <= n; i++)scanf("%lf%lf",&x[i],&y[i]); memset(g, 0, sizeof(g)); memset(a, 0, sizeof(a)); memset(b, 0, sizeof(b)); for(int i = 0; i <= n; i++){ for(int j = i+1; j <= n; j++){ if(!i)g[i][j] = 1<<(j-1); else if(build(i, j)){ g[i][j] |= 1<<(i-1); g[i][j] |= 1<<(j-1); for(int k = 1; k <= n; k++) if(check(i, j, k))g[i][j] |= (1<<(k-1)); } } } memset(dp, 127, sizeof(dp)); dp[0] = 0; for(int s = 0; s < (1<<n); s++) for(int i = 0; i <= n; i++) for(int j = i; j <= n; j++) dp[s|g[i][j]] = min(dp[s|g[i][j]], dp[s]+1); printf("%d ",dp[(1<<n)-1]); } return 0; }

View Code
O（N*2^N)，
#include <bits/stdc++.h> using namespace std; const int M = 20; double x[M], y[M], a[M][M], b[M][M]; int g[M][M], dp[1<<20]; const double eps = 1e-6; inline bool build(int i, int j){ a[i][j] = (y[i]/x[i] - y[j]/x[j]) / (x[i] - x[j]); if(a[i][j] >= 0)return false; b[i][j] = (y[i] - a[i][j]*x[i]*x[i]) / x[i]; return 1; } inline bool check(int i, int j, int k){ double tmp = a[i][j]*x[k]*x[k] + b[i][j] * x[k]; if(fabs(tmp - y[k]) < eps) return 1; return 0; } inline int min(int a, int b){ return a < b ? a : b; } int down(int s){ int i = 0; while(!(s&(1<<i)))i++; return i+1; } int main() { // freopen("angrybirds.in","r",stdin); // freopen("angrybirds.out","w",stdout); int T, n, m, cnt = 0; scanf("%d",&T); while(T--){ scanf("%d%d",&n,&m); for(int i = 1; i <= n; i++)scanf("%lf%lf",&x[i],&y[i]); memset(g, 0, sizeof(g)); for(int i = 1; i <= n; i++){ for(int j = i+1; j <= n; j++){ if(build(i, j)){ for(int k = 1; k <= n; k++) if(check(i, j, k))g[i][j] |= (1<<(k-1)); } } } for(int i = 1; i <= (1<<n); i++)dp[i] = 28; dp[0] = 0; for(int s = 1; s < (1<<n); s++){ int i = down(s); dp[s] = min(dp[s], dp[s-(1<<(i-1))]+1); for(int j = i+1; j<= n; j++){ int ss = (s&g[i][j]); dp[s] = min(dp[s], dp[s^ss]+1); } } printf("%d ",dp[(1<<n)-1]); } return 0; }

View Code
查看全文

相关阅读:
二分法检索数组
 Linux安装CDH
myeclipse操作hdfs
Linux安装hbase
Linux安装zookeeper
Linux安装msql
fluem全分布环境搭建
 bash: jps: 未找到命令...
自动化项目Jenkins持续集成
 linux卸载mysql====安装新的虚拟机自带的基本都要卸载！？ mysql tomcat java Python可以不用卸载

原文地址：https://www.cnblogs.com/EdSheeran/p/9061037.html

P2822 组合数问题

题目描述

输入输出格式

输入输出样例

说明

P2827 蚯蚓

题目描述

输入输出格式

输入输出样例

说明

P2831 愤怒的小鸟

题目描述

输入输出格式

输入输出样例

说明