问题 A: 老光棍
题目描述
L君和G君在玩一个游戏。G君写下一个字符串A,L君将其复制一遍连接到A串后面得到字符串B,G君又在B的任意位置(包括首尾)插入一个字符得到字符串C。现在你得到了C,请你找出A。
输入
第一行一个整数T,表示有T组数据
每组数据第一行一个整数 n,表示字符串 C 的长度。
每组数据第二行 n 个大写字母,表示字符串 C。
输出
若不存在可能的字符串 A,输出一行“NOT POSSIBLE” ;若存在多个不同的字符串 A 满足条件,输出一行“NOT UNIQUE” ;否则输出一行为满足条件的字符串 A。
样例输入
1 5 ZGZGZ
样例输出
NOT UNIQUE
提示
对于50%的数据,满足2 ≤ n ≤ 2000。
对于100%的数据,满足T ≤ 10,2 ≤ n ≤ 1000001。
部分数据随机。
题解:O(n) 枚举长度, O(1)hash查询是否满足, 如果前半部分可以去掉一个, 后半部分也可以去掉一个, 那么还要比较两个模板是否一样, 那么要去掉,判断细节比较多

#include <iostream> #include<cstdio> using namespace std; const int bas = 2333, maxn = 1000005; int n, rightpos,has[maxn], base[maxn]; char s[maxn]; void init(){ base[0] = 1; for(int i = 1; i <= n; i++) has[i] = has[i-1] * bas + s[i-1], base[i] = base[i-1] * bas; } bool check(int pos){ int st1, ed1, a, b , c, d; if(pos == 1){ a = has[n/2+1]-has[1]*base[n/2], c = has[n] - has[n/2+1]*base[n/2]; b = d = 0; } else if(pos == n){ a = has[n/2], c = has[n-1] - has[n/2] * base[n/2]; b = d = 0; } else if(pos == n/2 +1){ a = has[n/2], c = has[n] - has[n/2+1]*base[n-n/2-1]; b = d = 0; } else if(pos <= n/2){ st1 = n/2 + 1; ed1 = n/2 + pos, a = has[pos-1], b = has[n/2+1] - has[pos]*base[n/2-pos+1]; c = has[ed1] - has[st1]*base[ed1-st1], d = has[n] - has[ed1]*base[n-ed1]; } else if(pos > n/2){ st1 = pos-n/2-1; a = has[st1], b = has[n/2] - has[st1]*base[n/2-st1]; c = has[pos-1] - has[n/2]*base[pos-1-n/2], d = has[n]-has[pos]*base[n-pos]; } if((a==c) && (b==d)){ rightpos = pos;return 1; } return 0; } int main() { int T; scanf("%d", &T); while(T--){ int cnt = 0; scanf("%d", &n); scanf("%s", s); init(); int fg1 = 0, fg2 = 0; if(n%2 == 0){ puts("NOT POSSIBLE"); continue; } for(int i = 1; i <= n/2; i++) if(check(i)){ fg1 = 1;break; } for(int i = n/2+2; i <= n; i++) if(check(i)){ fg2 = 1; break; } if(fg1 && fg2) if(check(n/2+1)) cnt = 1; else cnt = 2; else if(fg1 || fg2) cnt = 1; if(check(n/2+1))cnt = 1; if(cnt == 1){ if(rightpos <= n/2){ for(int i = 1; i <= n/2+1; i++) if(i!=rightpos)printf("%c",s[i-1]); } else { for(int i = n/2+1; i <= n; i++) if(i!=rightpos)printf("%c", s[i-1]); } printf(" "); } else if(cnt > 1)puts("NOT UNIQUE"); else puts("NOT POSSIBLE"); } }
问题 B: 饼干
题目描述
佩琪和贝茜是好朋友。
佩琪最喜欢吃饼干了!但是现在他不准备自己吃,她决定和贝茜分享自己的饼干。佩琪有四种口味的饼干,分别是巧克力味、香草味、红豆味和椰子味。可惜的是,佩琪已经把椰子味的饼干全吃光了,所以现在只剩下前三种了233。。。
巧克力味饼干能带来A的美味度,香草味饼干能带来B的美味度,而红豆味饼干可以带来A+B的美味度。
佩琪会拿出不多于N块饼干作为送给贝茜的礼物。
为了显得真诚,她想让她拿出的饼干的美味度之和恰好为K。
为了显得体面,她决定用一个精美的盒子来装这些饼干。盒子内部有N个位置,每个位置都可以放一块饼干,或者不放。
现在佩琪想知道有多少种方案可以既显得真诚又显得体面。两种方案不同,当且仅当盒子中某个位置放置的饼干味道不同,或者一个放了饼干而另一个没有。
佩琪自己当然不会做啦,所以她决定请你来帮她解决这个问题。为了防止答案过大,你只需要告诉她答案对998244353取模的结果就行了。
输入
输入只有一行,包含四个整数,分别为N、A、B、K。
输出
输出一行一个整数,即答案对998244353取模的结果。
样例输入
4 1 2 5
样例输出
40
提示
对于前30%的数据,1≤N≤10,0≤K≤500
对于前50%的数据,1≤N≤1000,0≤K≤3000;
对于前80%的数据,1≤N≤1e5,0≤K≤2e10;
对于100%的数据,1≤N≤1e7,0≤K≤1e15,0≤A,B ≤1e5。
题解:我们可以求出n个盘子里放m个苹果的方案, 美味度可以枚举a的数量,b的数量也确定了, 那么a+b怎么办呢?
我们发现没有限制的放a, 没有限制的放b, 有些就会又放a又放b, 相当于a+b, 是不是很妙? 所以方案数 = C(a) * C(b) 。
还要, 这又是一道细节多的要死的题;

#include<iostream> #include<cstdio> #define p 998244353 #define ll long long using namespace std; const int maxn = 1e7 + 5; ll fac[maxn]; ll a, b, k, n; ll ans; ll mi(long long a,long long b) { long long anss=1; for(;b;b>>=1,a=a*a%p) if(b&1) anss=anss*a%p; return anss; } ll exgcd(ll a, ll b, ll &x, ll &y){ if(b == 0){ x=1;y=0;return a; } ll x0, y0; ll d = exgcd(b, a%b, x0, y0); x = y0; y = x0 - (a/b)*y0; return d; } ll in(ll a){ ll x, y; exgcd(a, p, x, y); return (x%p + p) %p; } ll C(ll pp, ll q){ return fac[n] * in(fac[pp]) % p * in(fac[n-pp]) % p * fac[n] %p * in(fac[q]) %p *in(fac[n-q]) % p; } int main ( ) { scanf ( "%lld%lld%lld%lld", &n, &a, &b, &k ); fac[0] = 1; for(ll i = 1; i <= n; i++) fac[i] = fac[i-1]*i % p; if(a==0&&b!=0) swap(a,b); if(!a && !b&&k!=0) ; else if(!a&&!b&&!k) ans=mi(4,n); else if(!b){ int fg = 0; if(k % a) fg = 1; int t = k/a; if(fg == 0) ans = fac[n] * in(fac[t]) % p * in(fac[n-t]) % p*mi(2,n)%p; } else { for(ll i = 0; i <= n; i++) if(i * a > k)break; else if( (k - a*i) % b == 0){ ll t = (k - a*i) / b; if(t <= n)ans = (ans + C(i , t)) % p; //printf("%lld ", ans); } } printf ("%lld", ans); return 0; }
问题 C: 空间宝石
题目描述
zP1nG很清楚自己打不过灭霸,所以只能在自己出的题里欺负他。
咳咳。
这一次他得到了空间宝石Tesseract。
世界之树连接着九界,此时灭霸和zP1nG都在九界的某个地方。而九界是相互无法到达的。zP1nG为了追杀灭霸,决定使用空间宝石的力量到达灭霸身边。因为zP1nG不擅长使用空间宝石,无法直接开一条从自己的位置到灭霸的位置的传送门,所以他只能无意识地使用空间宝石的力量。zP1nG想知道,在自己胡乱地使用空间宝石后,通过传送门到达灭霸的位置最少需要多长时间。
具体地,九界的编号为0~8,共有n道传送门,第i道传送门为优先级为pi,由ui到vi,需要花费wi个时间的单向门。传送的规则为:zP1nG按顺序穿过的传送门的优先级必须是单调不降的。例如,zP1nG穿过了三道传送门到达灭霸的位置,这三道传送门的优先级分别为1→2→2即为一种合法的方式,而优先级分别为1→2→1是不合法的。
zP1nG会使用q次宝石的力量来尝试进行传送:其中第i次尝试会打开数道传送门,这些传送门的优先级会形成si个区间。例如,在某次尝试中zP1nG打开了三个区间[1,2],[4,7],[9,10],那么优先级在这三个区间内的传送门将全部被打开并允许zP1nG穿过。你需要告诉zP1nG在此情况下从自己的位置zi到达灭霸所在处ti所需的最短时间。尝试结束后所有传送门会关闭。
输入
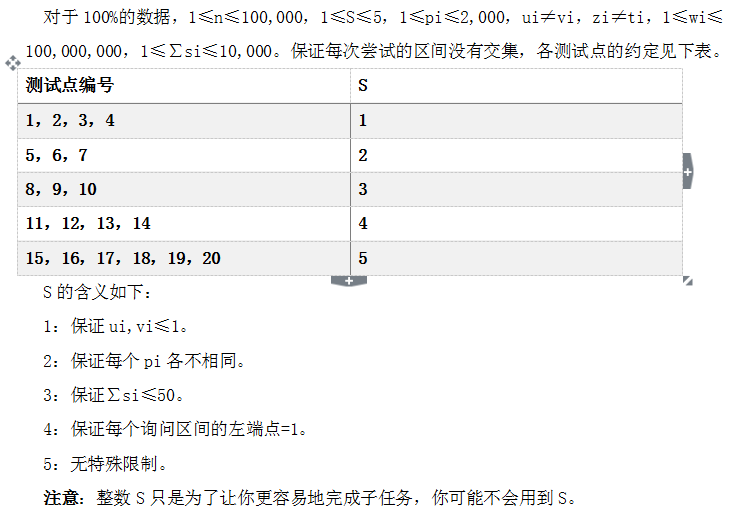
第1行包含两个正整数n和S,S的含义见数据范围与约定所述。
第2至n+1行每行包含4个正整数pi,ui,vi,wi。
第n+2行包含一个正整数q。
第n+3至第n+q+2行每行若干个正整数,其中前三个数为zi,ti,si,之后为2*si个正整数,表示每个区间的左右端点。
各变量具体含义见题目描述所述。
输出
对于zP1nG进行的每次尝试,输出一行一个数表示从zP1nG的位置到灭霸的位置所需的最短时间,如果zP1nG无法到达灭霸的位置则输出-1。
样例输入
6 2
1 2 4 1
2 1 3 3
3 1 2 2
4 3 4 5
5 2 4 3
6 1 4 2
4
1 4 1 1 3
1 4 1 1 4
1 4 2 5 5 2 3
1 4 1 1 6
样例输出
-1
8
5
2
提示
题解:这是一个神奇的解法,我们发现矩阵乘法是
a[i][j] = sum( b[i][k] + c[k][j] ); 如果把他改成a[i][j] = min( b[i][k] + c[k][j] ), 是不是就成Floyd了;
表示从i 到 j的最短路;那么优先级怎么办?——线段树;
每个优先级开一棵线段树,只能从优先级低的地方更新过来,所以询问的时候排一道序,然后用线段树合并,因为矩阵a[i][j]表示的是从i到j,所以必须要按优先级更新(思考为什么)

#include <bits/stdc++.h> using namespace std; #define maxn 10005 #define inf 1000000008 const int lim = 2005; struct Q{ int l, r; }q[maxn]; /*struct Edge{ int p, u, v, w; }e[maxn]; bool cmp2(Edge a, Edge b){ return a.p < b.p; }*/ bool cmp(const Q &a,const Q &b){ return a.l < b.l; } int tot; struct Maxtri{ int dis[10][10]; void init(){ for(int i = 0; i <= 8; i++) for(int j = 0; j <= 8; j++) dis[i][j] = (i == j) ? 0 : inf; } }G[lim+1]; Maxtri merge(Maxtri a, Maxtri b){ Maxtri c; c.init(); for(int k = 0; k < 9; k++) for(int i = 0; i < 9; i++) for(int j = 0; j < 9; j++) c.dis[i][j] = min(c.dis[i][j], a.dis[i][k]+b.dis[k][j]); return c; }; struct Node { Node * ls, * rs; Maxtri now; }pool[lim << 2], *tail = pool, *root; Node * build(int l = 1, int r = lim){ Node * nd = ++tail; if(l == r)nd -> now = G[l]; else { int m = (l + r) >> 1; nd -> ls = build(l, m); nd -> rs = build(m+1, r); nd -> now = merge(nd -> ls -> now, nd -> rs ->now); } return nd; } #define Ls l, mid, nd -> ls #define Rs mid+1, r, nd -> rs Maxtri query(int L, int R, int l = 1, int r = lim, Node * nd = root){ if(L <= l && R >= r)return nd->now; int mid = (l + r) >> 1; Maxtri ans; bool fg = 0; if(L <= mid){ ans = query(L, R, Ls); fg = 1; } if(R > mid) if(fg) ans = merge(ans, query(L, R, Rs)); else ans = query(L, R, Rs); return ans; } int main(){ int cas, n, S; scanf("%d%d", &n, &S); for(int i = 1; i <= lim; i++)G[i].init(); for(int i = 1; i <= n; i++){ int p, u, v, w; scanf("%d%d%d%d", &p, &u, &v, &w); G[p].dis[u][v] = min(G[p].dis[u][v], w); } for(int t = 1; t <= lim; t++) for(int k = 0; k < 9; k++) for(int i = 0; i < 9; i++) for(int j = 0; j < 9; j++) G[t].dis[i][j] = min(G[t].dis[i][j], G[t].dis[i][k]+G[t].dis[k][j]); root = build(); scanf("%d", &cas); while(cas--){ int st, ed, siz; scanf("%d%d%d", &st, &ed, &siz); for(int i = 1; i <= siz; i++) scanf("%d%d", &q[i].l, &q[i].r); sort(q+1, q+1+siz, cmp); Maxtri ans = query(q[1].l, q[1].r); for(int i = 2; i <= siz; i++){ ans = merge(ans, query(q[i].l, q[i].r)); } ans.dis[st][ed] < inf ? printf("%d ", ans.dis[st][ed]) : puts("-1"); } }
