P1273 有线电视网
题目描述
某收费有线电视网计划转播一场重要的足球比赛。他们的转播网和用户终端构成一棵树状结构,这棵树的根结点位于足球比赛的现场,树叶为各个用户终端,其他中转站为该树的内部节点。
从转播站到转播站以及从转播站到所有用户终端的信号传输费用都是已知的,一场转播的总费用等于传输信号的费用总和。
现在每个用户都准备了一笔费用想观看这场精彩的足球比赛,有线电视网有权决定给哪些用户提供信号而不给哪些用户提供信号。
写一个程序找出一个方案使得有线电视网在不亏本的情况下使观看转播的用户尽可能多。
输入输出格式
输入格式:
输入文件的第一行包含两个用空格隔开的整数N和M,其中2≤N≤3000,1≤M≤N-1,N为整个有线电视网的结点总数,M为用户终端的数量。
第一个转播站即树的根结点编号为1,其他的转播站编号为2到N-M,用户终端编号为N-M+1到N。
接下来的N-M行每行表示—个转播站的数据,第i+1行表示第i个转播站的数据,其格式如下:
K A1 C1 A2 C2 … Ak Ck
K表示该转播站下接K个结点(转播站或用户),每个结点对应一对整数A与C,A表示结点编号,C表示从当前转播站传输信号到结点A的费用。最后一行依次表示所有用户为观看比赛而准备支付的钱数。
输出格式:
输出文件仅一行,包含一个整数,表示上述问题所要求的最大用户数。
输入输出样例
说明
样例解释
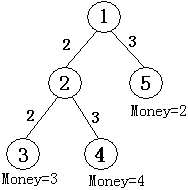
如图所示,共有五个结点。结点①为根结点,即现场直播站,②为一个中转站,③④⑤为用户端,共M个,编号从N-M+1到N,他们为观看比赛分别准备的钱数为3、4、2,从结点①可以传送信号到结点②,费用为2,也可以传送信号到结点⑤,费用为3(第二行数据所示),从结点②可以传输信号到结点③,费用为2。也可传输信号到结点④,费用为3(第三行数据所示),如果要让所有用户(③④⑤)都能看上比赛,则信号传输的总费用为:
2+3+2+3=10,大于用户愿意支付的总费用3+4+2=9,有线电视网就亏本了,而只让③④两个用户看比赛就不亏本了。
题解:裸的树上背包,和树上染色差不多:https://www.cnblogs.com/EdSheeran/p/9353225.html

#include<bits/stdc++.h> using namespace std; const int M = 3005; const int inf = -1e8; int h[M], siz[M], val[M], tot, dp[M][M], dep[M]; int n, m; struct edge{int v, nxt, w;}G[M << 2]; void add(int u, int v, int w){ G[++tot].v = v; G[tot].w = w; G[tot].nxt = h[u]; h[u] = tot; } void dfs(int u, int f){ dp[u][0] = 0; for(int i = h[u]; i; i = G[i].nxt){ int v = G[i].v; if(v == f)continue; dfs(v, u); siz[u] += siz[v]; for(int q = siz[u]; q; q--) for(int p = min(siz[v], q); p; p--){ if(dp[u][q - p] > inf) dp[u][q] = max(dp[u][q], dp[u][q - p] + dp[v][p] - G[i].w); } } if(u > n - m){ siz[u] = 1; dp[u][1] = val[u]; } //printf(" %d ",u); //for(int i = 0; i <= n; i++)printf("%d ", dp[u][i]); } int main(){ scanf("%d%d", &n, &m); memset(dp, 0x8f, sizeof(dp)); int x, u, v, w; for(int i = 1; i <= n - m; i++){ scanf("%d", &x); while(x--){ scanf("%d%d", &v, &w); add(i, v, w);///add(v, u, w); } } for(int i = n - m + 1; i <= n; i++)scanf("%d", val + i); dfs(1, 0); int ans = 0; for(int v = m; v; v--) if(dp[1][v] >= 0){ ans = v;break; } printf("%d ", ans); } /* 8 4 2 2 2 4 5 2 3 4 7 2 2 5 4 6 5 1 8 7 2 3 9 12 */
题目描述
国际象棋是世界上最古老的博弈游戏之一,和中国的围棋、象棋以及日本的将棋同享盛名。据说国际象棋起源于易经的思想,棋盘是一个8 imes 88×8大小的黑白相间的方阵,对应八八六十四卦,黑白对应阴阳。
而我们的主人公小Q,正是国际象棋的狂热爱好者。作为一个顶尖高手,他已不满足于普通的棋盘与规则,于是他跟他的好朋友小W决定将棋盘扩大以适应他们的新规则。
小Q找到了一张由N×M个正方形的格子组成的矩形纸片,每个格子被涂有黑白两种颜色之一。小Q想在这种纸中裁减一部分作为新棋盘,当然,他希望这个棋盘尽可能的大。
不过小Q还没有决定是找一个正方形的棋盘还是一个矩形的棋盘(当然,不管哪种,棋盘必须都黑白相间,即相邻的格子不同色),所以他希望可以找到最大的正方形棋盘面积和最大的矩形棋盘面积,从而决定哪个更好一些。
于是小Q找到了即将参加全国信息学竞赛的你,你能帮助他么?
输入输出格式
输入格式:
包含两个整数NN和MM,分别表示矩形纸片的长和宽。接下来的NN行包含一个N ×M的0101矩阵,表示这张矩形纸片的颜色(00表示白色,11表示黑色)。
输出格式:
包含两行,每行包含一个整数。第一行为可以找到的最大正方形棋盘的面积,第二行为可以找到的最大矩形棋盘的面积(注意正方形和矩形是可以相交或者包含的)。
输入输出样例
说明
对于20\%20%的数据,N, M ≤ 80N,M≤80
对于40\%40%的数据,N, M ≤ 400N,M≤400
对于100\%100%的数据,N, M ≤ 2000N,M≤2000
题解:一道毒瘤单调栈,我们可以预处理(i,j)向上最多扩张多少个,当第(i, j)确定后,若(i + 1, j)和他不同,那他上面合法部分一定与i的部分互异(这是此题关键);
然后就变成了一个求01最大自矩阵的O(N*M)的单调栈算法了;模版:https://www.cnblogs.com/EdSheeran/p/8459824.html

#include<bits/stdc++.h> using namespace std; const int M = 1005; struct Maxtri{int h, w, id;}tp[M]; bool a[M][M]; int up[M][M], t; int pf(int a){return a*a;} int main(){ int n, m, ans = 0, ans2 = 0; scanf("%d%d", &n, &m); for(int i = 1; i <= n; i++) for(int j = 1; j <= m; j++){ scanf("%d", &a[i][j]); } for(int i = 1; i <= m; i++)up[n][i] = 1; for(int i = n - 1; i; i--) for(int j = 1; j <= m; j++) up[i][j] = (a[i][j] ^ a[i + 1][j]) ? up[i + 1][j] + 1 : 1; for(int i = 1; i <= n; i++){ t = 0; for(int j = 1; j <= m; j++){ int w = 0; if(a[i][tp[t].id] ^ a[i][j] == 0) while(t){ w += tp[t].w; ans = max(ans, w * tp[t].h); ans2 = max(ans2, pf(min(tp[t].h, w))); t--; } w = 0; if(tp[t].h > up[i][j]){ while(t && tp[t].h > up[i][j]){ w += tp[t].w; ans = max(ans, w * tp[t].h); ans2 = max(ans2, pf(min(tp[t].h, w))); t--; } } tp[++t].h = up[i][j], tp[t].id = j, tp[t].w = w + 1; w = 0; if(j == m && t){ while(t){ w += tp[t].w; ans = max(ans, w * tp[t].h); ans2 = max(ans2, pf(min(tp[t].h, w))); t--; } } } } printf("%d %d ", ans2, ans); }
题目描述
上午的训练结束了,THU ACM小组集体去吃午餐,他们一行N人来到了著名的十食堂。这里有两个打饭的窗口,每个窗口同一时刻只能给一个人打饭。由于每个人的口味(以及胃口)不同,所以他们要吃的菜各有不同,打饭所要花费的时间是因人而异的。另外每个人吃饭的速度也不尽相同,所以吃饭花费的时间也是可能有所不同的。
THU ACM小组的吃饭计划是这样的:先把所有的人分成两队,并安排好每队中各人的排列顺序,然后一号队伍到一号窗口去排队打饭,二号队伍到二号窗口去排队打饭。每个人打完饭后立刻开始吃,所有人都吃完饭后立刻集合去六教地下室进行下午的训练。
现在给定了每个人的打饭时间和吃饭时间,要求安排一种最佳的分队和排队方案使得所有人都吃完饭的时间尽量早。
假设THU ACM小组在时刻0到达十食堂,而且食堂里面没有其他吃饭的同学(只有打饭的师傅)。每个人必须而且只能被分在一个队伍里。两个窗口是并行操作互不影响的,而且每个人打饭的时间是和窗口无关的,打完饭之后立刻就开始吃饭,中间没有延迟。
现在给定N个人各自的打饭时间和吃饭时间,要求输出最佳方案下所有人吃完饭的时刻。
输入输出格式
输入格式:
第一行一个整数N,代表总共有N个人。
以下N行,每行两个整数 Ai,Bi。依次代表第i个人的打饭时间和吃饭时间。
输出格式:
一个整数T,代表所有人吃完饭的最早时刻。
输入输出样例
说明
所有输入数据均为不超过200的正整数。
题解:贪心+DP;一道好题;
首先顺序的确定是按吃饭时间的大在前确定的,DP考虑在1、2号窗口吃饭;
dp[i][j] 表示第i个人打完饭,在1号窗口总的打饭时间为 j 的最早结束时间;
如果他在一号窗口,就是 max(dp[i][j - p[i].a], j + p[i].b),可能是之前的时间更慢,也可能当前的最慢;
同理,在二号窗口,就是max(dp[i][j], sum[i] - j + p[i].b),这个我们可以通过一个前缀和确定二号的时间;
然后两者取min

#include<bits/stdc++.h> using namespace std; const int M = 205; struct Point{int a, b;}p[M]; bool cmp(Point s, Point t){ return s.b > t.b; } int dp[M][M*M], sum[M]; int main(){ int n, ans = 1e9; scanf("%d", &n); for(int i = 1; i <= n; i++)scanf("%d%d", &p[i].a, &p[i].b); sort(p + 1, p + 1 + n, cmp); for(int i = 1; i <= n; i++) sum[i] = sum[i - 1] + p[i].a; memset(dp, 127, sizeof(dp)); dp[0][0] = 0; for(int i = 1; i <= n; i++) for(int j = 0; j <= sum[i]; j++){ dp[i][j] = max(dp[i - 1][j], sum[i] - j + p[i].b); if(j >= p[i].a) dp[i][j] = min(dp[i][j], max(dp[i - 1][j - p[i].a], j + p[i].b)); } for(int i = 0; i <= sum[n]; i++)ans = min(ans, dp[n][i]); printf("%d ", ans); }
题目描述
这次小可可想解决的难题和中国象棋有关,在一个N行M列的棋盘上,让你放若干个炮(可以是0个),使得没有一个炮可以攻击到另一个炮,请问有多少种放置方法。大家肯定很清楚,在中国象棋中炮的行走方式是:一个炮攻击到另一个炮,当且仅当它们在同一行或同一列中,且它们之间恰好 有一个棋子。你也来和小可可一起锻炼一下思维吧!
输入输出格式
输入格式:
一行包含两个整数N,M,之间由一个空格隔开。
输出格式:
总共的方案数,由于该值可能很大,只需给出方案数模9999973的结果。
输入输出样例
说明
样例说明
除了3个格子里都塞满了炮以外,其它方案都是可行的,所以一共有2*2*2-1=7种方案。
数据范围
100%的数据中N和M均不超过100
50%的数据中N和M至少有一个数不超过8
30%的数据中N和M均不超过6
题解:此题关键是当前行与上一行的状态无关,这样就和以往的DP不同;
一行、一列最多放2个炮,影响这行的是之前每列放了多少个炮;
dp[i][j]表示有i列放了1个, j列放了2个;
然后转移就是细节比较多的分类讨论+数学计算;

#include<bits/stdc++.h> using namespace std; #define ll long long const ll mod = 9999973; ll dp[105][105][105]; inline ll moc(ll a){return a >= mod ? a - mod : a;} int main(){ int n, m; ll ans = 0; scanf("%d%d", &n, &m); int u = 0; dp[0][0][0] = 1; for(int k = 0; k < n; k++){ memset(dp[u^1], 0, sizeof(dp[u^1])); for(int j = 0; j <= m; j++) for(int i = 0; i <= m - j; i++) if(dp[u][i][j]){ ll t = dp[u][i][j]; dp[u^1][i][j] = moc(dp[u^1][i][j] + t); if(m-i-j > 0) dp[u^1][i+1][j] = moc(dp[u^1][i+1][j] + t * 1LL*(m-i-j) % mod); if(m-i-j > 1) dp[u^1][i+2][j] = moc(dp[u^1][i+2][j] + t * 1LL*(m-i-j)*(m-i-j-1)/2 % mod); if(i) dp[u^1][i-1][j+1] = moc(dp[u^1][i-1][j+1] + t * 1LL*i % mod); if(i > 1) dp[u^1][i-2][j+2] = moc(dp[u^1][i-2][j+2] + t * 1LL*i*(i-1)/2 % mod); if(m-i-j && i) dp[u^1][i][j+1] = moc(dp[u^1][i][j+1] + t * 1LL*(m-i-j)*i % mod); } u ^= 1; } for(int j = 0; j <= m; j++) for(int i = 0; i <= m - j; i++) ans = (ans + dp[u][j][i]) % mod;//, printf("%d %d %lld ",i,j,dp[u][i][j]); printf("%lld ", ans); }
