
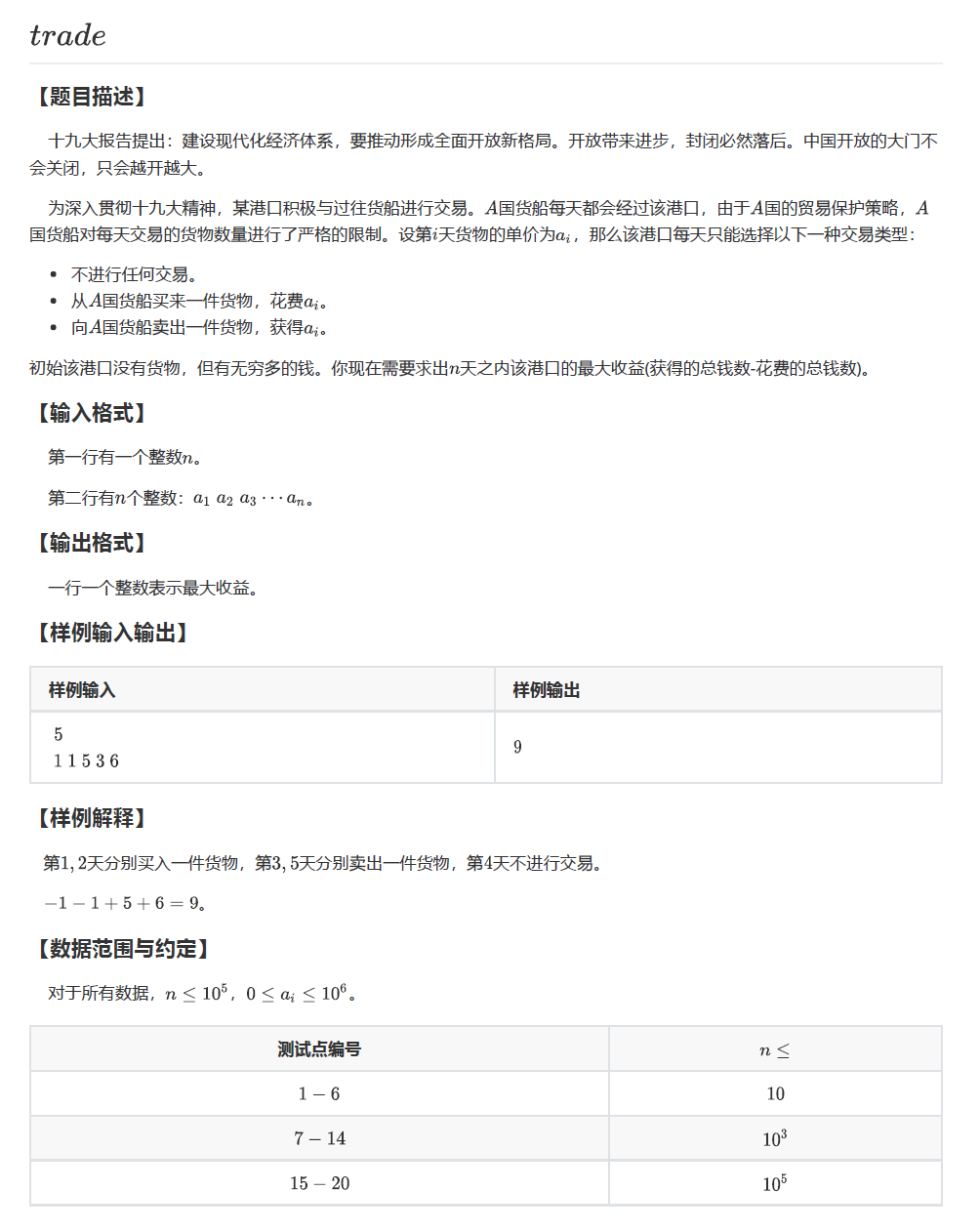



题解:
第一题:其实上次做过一次,但是这次搞了半天都没搞出来;
这是典型的后悔贪心,我们开两个小根堆,第一个堆存现在有那些可以卖出去,第二个后悔堆存卖出的;
如果取可以第一个堆的更优,我们加上利润,把这个卖出的物品丢掉,然后把物品卖出放进后悔堆,表示我当前这个这个物品或许应该买进,对后面的贡献更大;
否则还是加上利润,然后我们把第二个堆的这个物品放回第一个堆,因为这个物品不是我们真正卖掉的,他只是中间的一个媒介(实际卖掉的是这个物品进第二个堆是堆1pop掉的物品),所以他是可以继续对后面产生贡献的;

#include<bits/stdc++.h> using namespace std; priority_queue <int, vector<int>, greater<int> > q1, q2; int a[100005], inf = 2e9; int main(){ freopen("trade.in","r",stdin); freopen("trade.out","w",stdout); int n; long long ans = 0; scanf("%d", &n); for(int i = 1; i <= n; i++){ scanf("%d", &a[i]); if(q1.empty() && q2.empty())q1.push(a[i]); else { int b1 = inf, b2 = inf; if(!q1.empty()) b1 = q1.top(); if(!q2.empty()) b2 = q2.top(); if(b1 >= a[i] && b2 >= a[i]) q1.push(a[i]); else if(b1 <= b2) { ans += 1LL*(a[i] - b1); q1.pop(); q2.push(a[i]); } else { ans += 1LL*(a[i] - b2); q1.push(b2); q2.pop(); q2.push(a[i]); } } } printf("%lld ", ans); }
第二题:打表+莫队


#include<bits/stdc++.h> using namespace std; #define ll long long #define RG register const int M2 = 1e5 + 5; ll ret[M2], fac[M2], vfac[M2]; const ll mod = 1e9 + 7; inline ll moc(ll a){return a >= mod ? a - mod : a;} ll ksm(ll a, int b){ ll ret=1; for(;b;b>>=1,a=a*a%mod) if(b&1)ret=ret*a%mod; return ret; } int N = 1e5, inv2, siz = 300, block[M2]; struct Query{int n, m, id;}q[M2]; bool cmp(Query a, Query b){return block[a.m] == block[b.m] ? a.n < b.n : a.m < b.m;} void init(){ fac[0] = vfac[0] = 1; for(ll i = 1; i <= N; i++) { fac[i] = fac[i - 1] * i % mod; block[i] = i/siz + 1; } inv2 = ksm(2, mod - 2); vfac[N] = ksm(fac[N], mod - 2); for(ll i = N - 1; i; i--) vfac[i] = vfac[i + 1] * (i + 1) % mod; } ll C(int n, int m){ if(m > n) return 0; return fac[n] * vfac[m] % mod * vfac[n-m] % mod; } int main(){ int id, Q; freopen("sum.in","r",stdin); freopen("sum.out","w",stdout); scanf("%d", &id); init(); scanf("%d", &Q); for(int i = 1; i <= Q; i++) scanf("%d%d", &q[i].n, &q[i].m), q[i].id = i; sort(q + 1, q + 1 + Q, cmp); int n = 0, m = 0; ll ans = 1; for(int i =1; i <= Q; i++){ while(q[i].m < m){ ans = (ans - C(n, m) + mod) % mod; m--; } while(q[i].n > n){ ans = (2LL*ans - C(n, m) + mod) % mod; n++; } while(q[i].m > m){ m++; ans = (ans + C(n, m)) % mod; } while(q[i].n < n){ n--; ans = (ans + C(n, m)) * inv2 % mod; } //if(i!=1)printf("%d %d %lld ", n,m,ans); ret[q[i].id] = ans; } for(int i = 1; i <= Q; i++)printf("%lld ", ret[i]); return 0; }
第三题:其实算一个模拟吧,二分+并查集合并
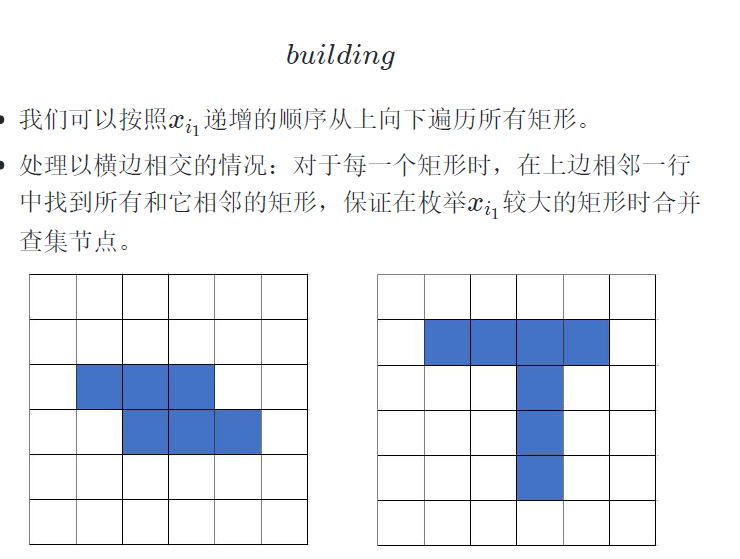
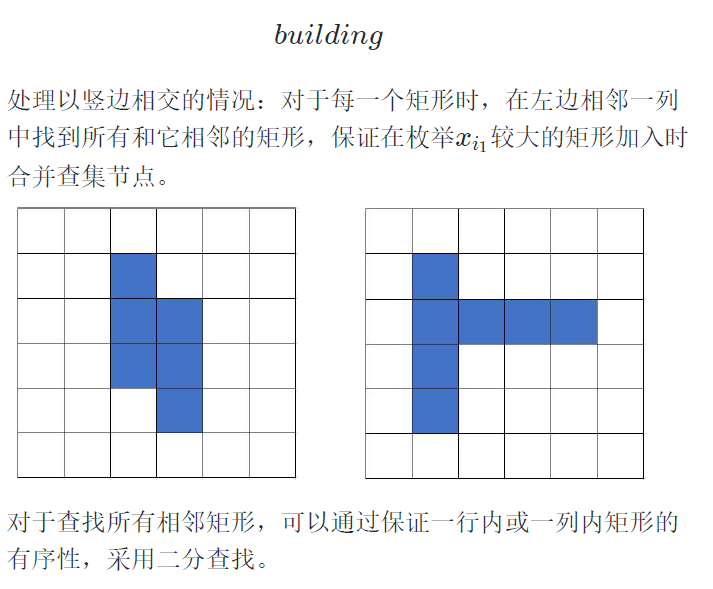

#include<bits/stdc++.h> using namespace std; #define For(a, b, c) for(int a=b;a<=c;a++) const int M = 1e5 + 10; int sum[M], cf[M], fa[M], mix, ans[M], scc[M]; struct Edge{int u, v;}; vector <Edge> G[M]; struct Node{ int id, mi, mx; bool operator < (const Node &rhs)const { return mi < rhs.mi || (mi == rhs.mi && mx < rhs.mx); } }; vector <Node> row[M], lie[M]; struct Init{int xs,ys,xe,ye;}p[M]; int find(int x){ if(x == fa[x]) return x; return fa[x] = find(fa[x]); } void uni(int x, int y){ int fx = find(x), fy = find(y); if(fx != fy) mix++, fa[fx] = fy; } int read(){ int x=0,f=1;char c=getchar(); while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*=f; } int main(){ freopen("building.in","r",stdin); freopen("building.out","w",stdout); int cas; scanf("%d", &cas); int n, m, k, Q; int xs,ys,ye,xe; scanf("%d%d%d%d", &n, &m, &k, &Q); For(i, 1, k){ xs = read(), ys = read(), xe = read(), ye = read(); p[i] = (Init){xs,ys,xe,ye}; if(xs == xe) sum[xs] += ye - ys + 1; else cf[xs]++, cf[xe+1]--; row[xs].push_back((Node){i, ys, ye}); lie[ys].push_back((Node){i, xs, xe}); } For(i, 1, n) sort(row[i].begin(), row[i].end()); For(i, 1, m) sort(lie[i].begin(), lie[i].end()); For(i, 1, k){ int dwn = p[i].xe + 1; int pos = upper_bound(row[dwn].begin(), row[dwn].end(), (Node){0, p[i].ye, m+1}) - row[dwn].begin() - 1; for(; pos >= 0 && row[dwn][pos].mx >= p[i].ys; pos--) G[dwn].push_back((Edge){i, row[dwn][pos].id}); int rg = p[i].ye + 1; pos = upper_bound(lie[rg].begin(), lie[rg].end(), (Node){0, p[i].xe, n+1}) - lie[rg].begin() - 1; for(; pos >= 0 && lie[rg][pos].mx >= p[i].xs; pos--) G[max(p[i].xs, lie[rg][pos].mi)].push_back((Edge){i, lie[rg][pos].id}); } int tot = 0; For(i, 1, k) fa[i] = i; For(i, 1, n){ tot += row[i].size(); int siz = G[i].size(); For(j, 0, siz-1){ int u = G[i][j].u, v = G[i][j].v; uni(u, v); } scc[i] = tot - mix; } For(i, 1, n) cf[i] += cf[i-1]; For(i, 1, n){ cf[i] += cf[i-1]; sum[i] += sum[i-1]; ans[i] = sum[i] + cf[i]; } while(Q--){ int opt, u; opt = read(), u = read(); printf("%d ", opt ? scc[u] : ans[u]); } }
