这些都是难度很大的DP,我自己没想出来了一道(而且考代码细节)
题目描述
给出一列数字,需要你添加任意多个逗号将其拆成若干个严格递增的数。如果有多组解,则输出使得最后一个数最小的同时,字典序最大的解(即先要满足最后一个数最小;如果有多组解,则使得第一个数尽量大;如果仍有多组解,则使得第二个数尽量大,依次类推……)。
输入输出格式
输入格式:
共一行,为初始的数字。
输出格式:
共一行,为拆分之后的数列。每个数之间用逗号分隔。行尾无逗号。
输入输出样例
[1] 3456 [2] 3546 [3] 3526 [4] 0001 [5] 100000101
[1] 3,4,5,6 [2] 35,46 [3] 3,5,26 [4] 0001 [5] 100,000101
说明
【题目来源】
lzn改编
【数据范围】
对于10%的数据,输入长度<=5
对于30%的数据,输入长度<=15
对于50%的数据,输入长度<=50
对于100%的数据,输入长度<=500
题解:一道好题,两次DP;这种有两个限制的都是先确定一维,再确定另一维
先正着做一次,dp[i]表示以i结尾的符合条件的并满足最后一个数最小的序列长度;
这样就可以确定最后一段的长度,我们再此基础上又反着做一次,求字典序最大的解

#include<cstdio> #include<string> #include<cstring> using namespace std; int dp[505]; char s[500]; bool check(int s1, int t1, int s2, int t2){ while(s[s2] == '0' && s2 <= t2)s2++; if(s2 > t2)return 0; while(s[s1] == '0' && s1 <= t1)s1++; if(s1 > t1)return 0; if(t2-s2>t1-s1) return 1; if(t2-s2<t1-s1) return 0; for(;s2<=t2; s2++, s1++){ if(s[s2] < s[s1])return 0; if(s[s2] > s[s1])return 1; } return 0; } int main(){ while(scanf("%s", s+1)){ int n = strlen(s + 1); if(n == 1 && s[1] == '0')break; for(int i = 1; i <= n; i++){ dp[i] = i; for(int j = i - 1; j; j--){ if(check(j-dp[j]+1, j, j+1, i)){ dp[i] = i - j; break; } } } int st = n-dp[n]; dp[st+1] = dp[n]; for(int i = st; i; i--){ if(s[i] == '0'){ dp[i]=dp[i+1]+1; continue; } for(int j = st+1; j > i; j--){ if(check(i, j-1, j, j+dp[j]-1)){ dp[i] = j - i; break; } } } int nw = 1; while(nw <= n){ int i; for(i = nw; i <= dp[nw]+nw-1; i++) printf("%c",s[i]); if(i!=n+1) printf(","); nw = i; } puts(""); } }
题目描述
小F 的学校在城市的一个偏僻角落,所有学生都只好在学校吃饭。学校有一个食堂,虽然简陋,但食堂大厨总能做出让同学们满意的菜肴。当然,不同的人口味也不一定相同,但每个人的口味都可以用一个非负整数表示。 由于人手不够,食堂每次只能为一个人做菜。做每道菜所需的时间是和前一道菜有关的,若前一道菜的对应的口味是a,这一道为b,则做这道菜所需的时间为(a or b)-(a and b),而做第一道菜是不需要计算时间的。其中,or 和and 表示整数逐位或运算及逐位与运算,C语言中对应的运算符为“|”和“&”。
学生数目相对于这个学校还是比较多的,吃饭做菜往往就会花去不少时间。因此,学校食堂偶尔会不按照大家的排队顺序做菜,以缩短总的进餐时间。
虽然同学们能够理解学校食堂的这种做法,不过每个同学还是有一定容忍度的。也就是说,队伍中的第i 个同学,最多允许紧跟他身后的Bi 个人先拿到饭菜。一旦在此之后的任意同学比当前同学先拿到饭,当前同学将会十分愤怒。因此,食堂做菜还得照顾到同学们的情绪。 现在,小F 想知道在满足所有人的容忍度这一前提下,自己的学校食堂做完这些菜最少需要多少时间。
输入输出格式
输入格式:
第一行包含一个正整数C,表示测试点的数据组数。 每组数据的第一行包含一个正整数N,表示同学数。 每组数据的第二行起共N行,每行包含两个用空格分隔的非负整数Ti和Bi,表示按队伍顺序从前往后的每个同学所需的菜的口味和这个同学的忍受度。 每组数据之间没有多余空行。
输出格式:
包含C行,每行一个整数,表示对应数据中食堂完成所有菜所需的最少时间。
输入输出样例
说明
对于第一组数据:
同学1允许同学2或同学3在他之前拿到菜;同学2允许同学3在他之前拿到菜;同学3比较小气,他必须比他后面的同学先拿菜……
一种最优的方案是按同学3、同学2、同学1、同学4、同学5做菜,每道菜所需的时间分别是0、8、1、6及1。
【数据规模和约定】
对于30%的数据,满足1 ≤ N ≤ 20。
对于100%的数据,满足1 ≤ N ≤ 1,000,0 ≤ Ti ≤ 1,000,0 ≤ Bi ≤ 7,1 ≤ C ≤ 5。
存在30%的数据,满足0 ≤ Bi ≤ 1。
存在65%的数据,满足0 ≤ Bi ≤ 5。
存在45%的数据,满足0 ≤ Ti ≤ 130。
题解:神奇的状压DP;以下题解摘自洛谷:


#include <iostream> #include <cstring> #include <cstdio> #include <algorithm> using namespace std; #define ll long long const int M = 1005, inf = 2e9; int dp[M][(1<<8) + 1][20]; //(a or b)-(a and b) int t[M], h[M]; int w(int a, int b){ if(a <= 0) return 0; return t[a] ^ t[b]; } void up(int &a, int b){ a = min(a, b); } int main(){ int n, T; scanf("%d", &T); while(T--){ scanf("%d", &n); for(int i = 1; i <= n; i++)scanf("%d%d", &t[i], &h[i]); memset(dp, 127, sizeof(dp)); dp[1][0][7] = 0; for(int i = 1; i <= n; i++){ for(int s = 0; s < (1<<8); s++){ for(int k = -8; k <= 7; k++){ if(dp[i][s][k + 8] > inf) continue; //printf("%d %d %d %d ", i, s, k, dp[i][s][k + 8]); if(s & 1) up(dp[i + 1][s >> 1][k + 7], dp[i][s][k + 8]); else { int limit = inf; for(int j = 0; j <= 7; j++) if(!(s & (1<<j))){ if(i + j > limit)continue; up(limit, i + j + h[i + j]); int z = w(i + k, i + j); up(dp[i][s |(1<<j)][j + 8], dp[i][s][k + 8] + z); } } } } } int ans = inf; for(int k = -8; k <= 0; k++) ans = min(ans, dp[n + 1][0][k + 8]); printf("%d ", ans); } }
题目描述
有一个a*b的整数组成的矩阵,现请你从中找出一个n*n的正方形区域,使得该区域所有数中的最大值和最小值的差最小。
输入输出格式
输入格式:
第一行为3个整数,分别表示a,b,n的值
第二行至第a+1行每行为b个非负整数,表示矩阵中相应位置上的数。每行相邻两数之间用一空格分隔。
输出格式:
仅一个整数,为a*b矩阵中所有“n*n正方形区域中的最大整数和最小整数的差值”的最小值。
输入输出样例
说明
问题规模
(1)矩阵中的所有数都不超过1,000,000,000
(2)20%的数据2<=a,b<=100,n<=a,n<=b,n<=10
(3)100%的数据2<=a,b<=1000,n<=a,n<=b,n<=100
题解:


#include <cstdio> #include <cstdlib> #include <ctime> #include <algorithm> #include <cstring> using namespace std; const int M = 1005; int lo[105], a[M][M][12], b[M][M][12]; int A, B, n; void init(){ for(int qi = 1; qi <= 10; qi++) for(int i = 1; i + (1<<qi) - 1 <= A; i++) for(int j = 1; j <= B; j++){ a[i][j][qi] = min(a[i][j][qi-1], a[i + (1<<(qi-1))][j][qi-1]); b[i][j][qi] = max(b[i][j][qi-1], b[i + (1<<(qi-1))][j][qi-1]); } } struct P{int v, id;}q1[M], q2[M]; int main(){ scanf("%d%d%d", &A, &B, &n); lo[0] = -1; for(int i = 1; i <= n; i++) lo[i] = lo[i/2] + 1; int pi = lo[n]; for(int i = 1; i <= A; i++) for(int j = 1; j <= B; j++){ scanf("%d", &a[i][j][0]); b[i][j][0] = a[i][j][0]; } init(); int mx = 2e9; for(int i = 1; i <= A - n + 1; i++){ int h1 = 1, h2 = 1, t1 = 0, t2 = 0; for(int j = 1; j <= B; j++){ int a1 = min(a[i][j][pi], a[i+n-1 - (1<<pi) + 1][j][pi]); int b1 = max(b[i][j][pi], b[i+n-1 - (1<<pi) + 1][j][pi]); if(j > n) mx = min(mx, q2[h2].v - q1[h1].v); if(h1 <= t1 && j - q1[h1].id + 1 > n)h1++; if(h2 <= t2 && j - q2[h2].id + 1 > n) h2++; while(h1 <= t1 && a1 <= q1[t1].v) t1--; while(h2 <= t2 && b1 >= q2[t2].v) t2--; q1[++t1].v = a1, q1[t1].id = j; q2[++t2].v = b1, q2[t2].id = j; //printf("%d %d %d %d %d ", mx, i, j, a1, b1); } mx = min(mx, q2[h2].v - q1[h1].v); } printf("%d ", mx); }
题目描述
传说很久以前,大地上居住着一种神秘的生物:地精。
地精喜欢住在连绵不绝的山脉中。具体地说,一座长度为N的山脉H可分为从左到右的N段,每段有一个独一无二的高度Hi,其中Hi是1到N之间的正整数。
如果一段山脉比所有与它相邻的山脉都高,则这段山脉是一个山峰。位于边缘的山脉只有一段相邻的山脉,其他都有两段(即左边和右边)。
类似地,如果一段山脉比所有它相邻的山脉都低,则这段山脉是一个山谷。
地精们有一个共同的爱好——饮酒,酒馆可以设立在山谷之中。地精的酒馆不论白天黑夜总是人声鼎沸,地精美酒的香味可以飘到方圆数里的地方。
地精还是一种非常警觉的生物,他们在每座山峰上都可以设立瞭望台,并轮流担当瞭望工作,以确保在第一时间得知外敌的入侵。
地精们希望这N段山脉每段都可以修建瞭望台或酒馆的其中之一,只有满足这个条件的整座山脉才可能有地精居住。
现在你希望知道,长度为N的可能有地精居住的山脉有多少种。两座山脉A和B不同当且仅当存在一个i,使得Ai≠Bi。由于这个数目可能很大,你只对它除以P的余数感兴趣。
输入输出格式
输入格式:
输入文件goblin.in仅含一行,两个正整数N, P。
输出格式:
输出文件goblin.out仅含一行,一个非负整数,表示你所求的答案对P取余之后的结果。
输入输出样例
说明

【数据规模和约定】
对于20%的数据,满足N≤10;
对于40%的数据,满足N≤18;
对于70%的数据,满足N≤550;
对于100%的数据,满足3≤N≤4200,P≤1e9。
题解:一道好题,神奇的转移,主要要抓住数据的性质
摘自https://www.cnblogs.com/ciao-sora/p/5988265.html
一个多月前“过”了这道题,还自欺欺人地认为懂了这道题,这直接导致了昨晚多校联测2的T3爆炸,现在想来简直是道水题,不过还是要有“懂得这题怎么做”的前提。。。地精部落这道题可以约化为另一个问题:对于n的排列,告诉你每个数相比于前一个数是大了、小了、还是都可以,求这样的排列的方案数。
先说这一题叭,看过很多其他人的题解,依然是云里雾里,因此我会写的详细一点。我的写法可能与其他人有些不同,但是本质是完全一样的。
首先令f(i, j)表示已经考虑完i的排列了,最后一个数是j,且它为山谷的方案数。这里特别注意!这个i的排列并不一定非要是闭区间[1, i]里的数!这种排列仅仅表示一个大小关系,一种相对的关系,有种离散化的感觉(也可以理解为考虑完i个数了,最后一个数是其中第j小的,且它为山谷的方案数)。这一点非常重要,一定要理解,如不理解可以先往下看,我后面会举个例子。类似地,令g(i, j)表示已经考虑完i的排列了,最后一个数是j,且它为山峰的方案数。那么状态转移方程就是:
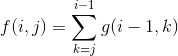 ①
①
为什么是这样呢?首先f数组的值一定是从g数组转移过来的,因为如果这个是山谷,那么上一个就是山峰。那么为什么等于后面那一串呢?考虑这个例子,7253,这是你填完最后一个数字3后的某个方案。很显然,这种方案应该属于状态f(4, 2),因为已经考虑4个数了,3是其中第2小的。那么f(4, 2)这种状态可以从g(3, 2)与g(3, 3)转移过来,在7253这个例子中,f(4, 2)是从g(3, 2)转移过来的,因为在725中,5是第2小的。那么前i - 1个数中,最小能小到多少呢?(当然是考虑最小的,因为越大,就越可能转移到当前状态,所以最大能大到第i - 1小)答案是能小到j。因为前i个数中第j小的,必然比前i - 1个数中第j小的要小!可以通过刚刚7253这个例子来感受一下,3是前4个数中第2小的,5是前3个数中第2小的。
这个弄懂了之后,我们又可以发现一个很容易发现、非常显然的结论:把一个符合条件的n的排列,对于没一个数i,将其改为n + 1 - i,新的排列依然符合条件,并且原来的山峰变成山谷,山谷变成山峰,因此有:
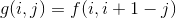 ②
②
联立①②,得

用一个辅助变量s,就可以O(1)转移了,最后ans = (f[n][1] + f[n][2] + ... + f[n][n]) * 2,因为f表示的是最后一个为山谷,根据那个显然的结论,可以得到等量的最后一个为山峰的方案数。在加一个滚动数组压缩空间就可以过了。

#include<bits/stdc++.h> using namespace std; int mod, n, f[2][5005]; int moc(int a){return a >= mod ? a - mod : a;} int main(){ scanf("%d%d", &n, &mod); f[1][1] = 1; int u = 1; for(int i = 2; i <= n; i++){ u ^= 1; memset(f[u], 0, sizeof(f[u])); for(int j = i - 1; j; j--) f[u][j] = moc(f[u][j + 1] + f[u ^ 1][i - j]); } int ans = 0; for(int i = 1; i <= n; i++) ans = moc(ans + 2 * f[u][i] % mod); printf("%d " ,ans); }
农夫约翰决定给站在一条线上的N(1 <= N <= 200,000)头奶牛制作一张全家福照片,N头奶牛编号1到N。
于是约翰拍摄了M(1 <= M <= 100,000)张照片,每张照片都覆盖了连续一段奶牛:第i张照片中包含了编号a_i 到 b_i的奶牛。但是这些照片不一定把每一只奶牛都拍了进去。
在拍完照片后,约翰发现了一个有趣的事情:每张照片中都有且仅有一只身上带有斑点的奶牛。约翰意识到他的牛群中有一些斑点奶牛,但他从来没有统计过它们的数量。 根据照片,请你帮约翰估算在他的牛群中最多可能有多少只斑点奶牛。如果无解,输出“-1”。
Input
输入输出格式
输入格式:
* Line 1: Two integers N and M.
* Lines 2..M+1: Line i+1 contains a_i and b_i.
输出格式:
* Line 1: The maximum possible number of spotted cows on FJ's farm, or -1 if there is no possible solution.
输入输出样例
说明
There are 5 cows and 3 photos. The first photo contains cows 1 through 4, etc.
From the last photo, we know that either cow 3 or cow 4 must be spotted. By choosing either of these, we satisfy the first two photos as well.
题解:貌似用差分约束会T,题解给了一种限制左右端点的巧妙做法;

这个解释可能好一些:https://www.cnblogs.com/Y-E-T-I/p/7240100.html

#include <cstdio> #include <cstdlib> #include <ctime> #include <algorithm> #include <cstring> using namespace std; const int M = 200005; int f[M], q[M], lf[M], rg[M]; int main(){ int n, m, x, y; scanf("%d%d", &n, &m); for(int i = 1; i <= n+1; i++) rg[i] = i-1; for(int i = 1; i <= m; i++){ scanf("%d%d", &x, &y); rg[y] = min(rg[y], x-1); lf[y+1] = max(lf[y+1], x); } for(int i = n; i; i--)rg[i] = min(rg[i], rg[i+1]); for(int i = 2; i <= n+1; i++) lf[i] = max(lf[i], lf[i-1]); int j = 1, h = 1, t = 1; q[1] = 0; for(int i = 1; i <= n+1; i++){ while(j<=rg[i]){ if(f[j] == -1) {j++;continue;} while(h <= t && f[j] > f[q[t]])t--; q[++t] = j; j++; } while(h <= t && q[h] < lf[i])h++; if(h <= t) f[i] = f[q[h]] + (i != n+1); else f[i] = -1; } printf("%d ", f[n+1]); }
