平时十七测

题解：

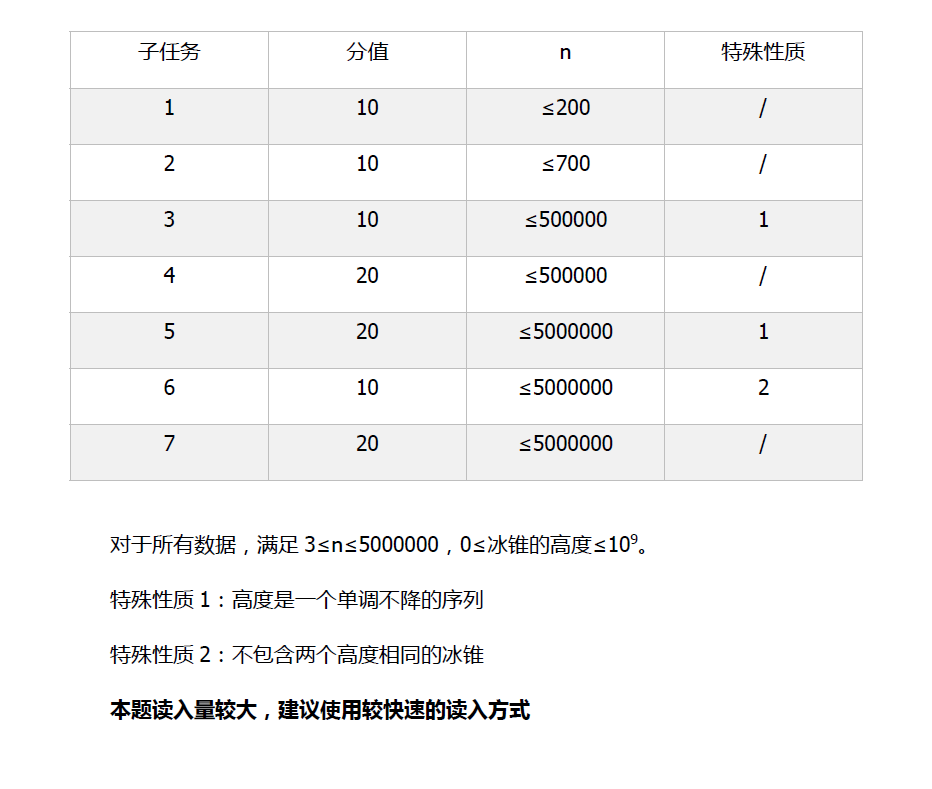
第一题：看数据范围是O（n）,而且很像单调栈；

如果不是环，维护一个单调递减的栈，弹栈的时候计算贡献，对于重复的元素，我们记一个size；

环怎么办，显然是拆了，从最高的地方拆，那么就不可能有跨过他的元素，这样搞一遍单调栈就可以了；

对于最高的元素再统计一下只有往外可以建边的贡献；

#include<bits/stdc++.h>
using namespace std;

const int M = 5e6 + 10;
int a[M], b[M], c[M];
struct node{int cnt, w;}q[M];
int read(){
    int x = 0; int f = 1; char c = getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c<='9'&&c>='0'){x=x*10+c-'0';c=getchar();}
    return x*=f;
}

int main(){
    freopen("jolyne.in","r",stdin);
    freopen("jolyne.out","w",stdout);
    int n = read(), mx = 0;
    long long ans = 0;
    for(int i = 1; i <= n; i++) {
        b[i] = read();
        if(b[i] > b[mx]) mx = i; 
    }
    int y = 0;
    for(int i = mx; i <= n; i++)
        a[++y] = b[i];
    for(int i = 1; i < mx; i++)
        a[++y] = b[i];
    mx = a[n];
    memset(b, 0, sizeof(b));b[n]=1;
    for(int i = n - 1; i > 1; i--){
        b[i] = a[i] >= mx;
        mx = max(a[i], mx);
    }
    mx = a[2];c[2] = 1;
    for(int i = 3; i <= n; i++){
        c[i] = a[i] >= mx;
        mx = max(a[i], mx);
    }
    int h = 1, t = 0;
    for(int i = 1; i <= n; i++){
        while(h <= t && a[i] > q[t].w){
            ans += q[t].cnt;
            t--;
        }
        if(h <= t && q[t].w == a[i]){
            ans += q[t].cnt;
            q[t].cnt++;
            if(h != t) ans++;
            continue;
        }
        else if(h <= t)ans++; 
        q[++t] = (node) { 1, a[i] };
        //printf("%d %d
", i, ans);
    }
    for(int i = 1; i <= n; i++) ans += (b[i] && !c[i]);
    printf("%lld
", ans);
}

第二题：DP， 这道题是一道思维题，如果一直想这个过程是怎么搞的，就GG了；

f(i,0)代表第一次到第i号房间所用步数，f(i,1)代表第二次到达房间所用步数

sum[i]：f[i][1]-f[i][0]的前缀和

f[i][0] = f[i-1][1] + 1;

f[i][1] = f[p[i]][1] - f[p[i]][0] + f[p[i]+1][1] - f[p[i]][0] + …… + f[i-1][1] - f[i-1][0] + f[i][0] + i - p[i] + 1 = sum[i-1] - sum[p[i] - 1] + f[i][0] + i - p[i] + 1;

#include<bits/stdc++.h>
using namespace std;
const int M = 1000005;
int a[M];
#define ll long long
ll f[M][2], sum[M];
const ll mod = 1e9 + 7;

int main(){
    freopen("rideon","r",stdin);
    freopen("rideon","w",stdout);
    int n;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
    f[1][0] = 0;
    f[1][1] = 1;
    sum[1] = 1;
       for(int i = 2; i <= n; i++)
    {
        f[i][0] = (f[i - 1][1] + 1)%mod;
        f[i][1] = ((f[i][0] + sum[i - 1]) % mod - sum[a[i] - 1] + i - a[i] + 1 + mod) % mod;
        sum[i] = (sum[i - 1] + f[i][1] - f[i][0]+mod)%mod;
        // cout <<i<<":"<< f[i][0] << " " << f[i][1] <<" "<<sum[i]<< endl;
    }
    ll ans = (f[n][1] + 1+mod)%mod;
    cout << ans<< endl;

}

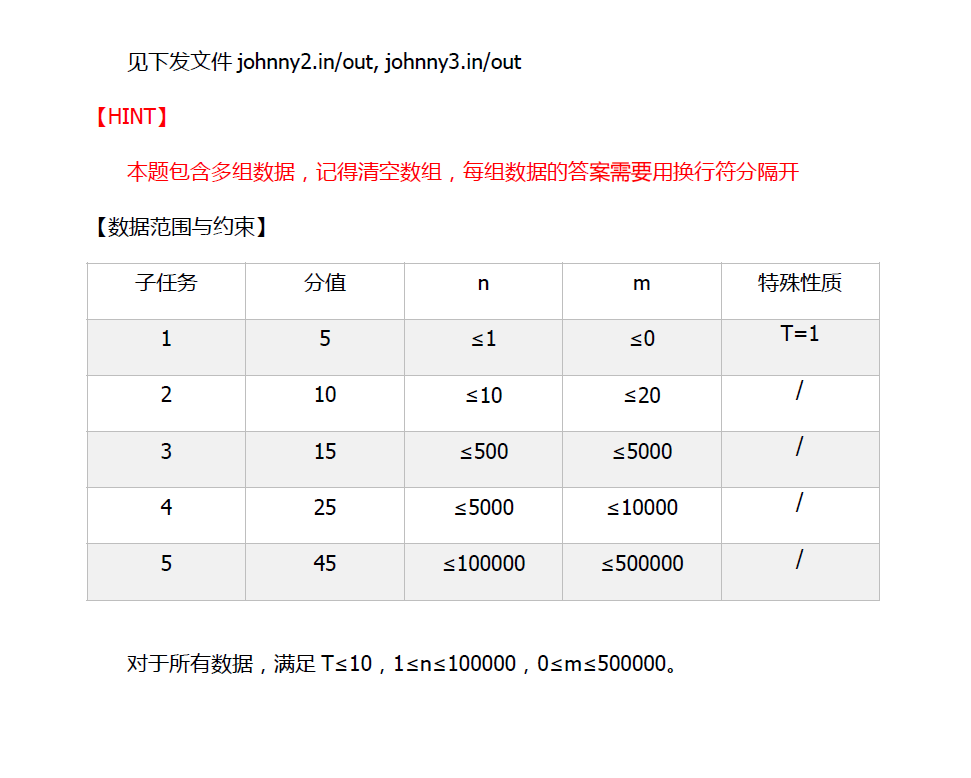
第三题：这道题很像AIRPORT，但是每次我都会忘记有一个叫拓扑的算法；

#include<bits/stdc++.h>
using namespace std;

const int INF=1e9;
const int N=5e5+10;
const int M=2e6+10;
int n,m,h,t,mn,ans;
int du[M],qs[M],w[M];
priority_queue<int>p,q; 

struct Tst
{
    int head[N],dis[N],du[N],tot;

    struct edge{int nxt, u, v;}G[M];

    inline void add(int x,int y){
        G[++tot].nxt = head[x]; head[x] = tot; G[tot].v = y; G[tot].u = x;
    }
    inline void clear(){
        tot = 0;
        memset(head, 0, sizeof(head));
        memset(du, 0, sizeof(du));
    }

    inline void solve(int S)
    {
        memset(dis,0,sizeof(dis));
        h=t=1;qs[1]=S;
        while(h<=t)
        {
            int x=qs[h++];
            for(int i=head[x];i;i=G[i].nxt)
            {
                int y=G[i].v;
                dis[y]=max(dis[y],dis[x]+1);
                du[y]--;
                if(!du[y])
                    qs[++t]=y;
            }
        }
    }
};
Tst A,B;

inline void dele(int x)
{
    q.push(x);
    while(!p.empty() && !q.empty() && q.top()==p.top())
    {
        q.pop();
        p.pop();
    }
}

int read(){
    int x = 0; int f = 1; char c = getchar();
    while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();}
    while(c<='9'&&c>='0'){x=x*10+c-'0';c=getchar();}
    return x*=f;
}
void init(){
    A.clear();
    B.clear();
    memset(du, 0, sizeof(du));
    while(!q.empty())q.pop();
    while(!p.empty())p.pop();
}


int main()
{
    freopen("johnny.in","r",stdin);
  freopen("johnny.out","w",stdout);
    int T;
    T = read();
    while(T--){
        init();
        n=read();m=read();
        for(int i=1;i<=m;++i)
        {
            int u,v;
            u=read();v=read();
            du[v]++;A.du[v]++;B.du[u]++;
            A.add(u,v);B.add(v,u);
        }
        for(int i=1;i<=n;++i)
        {
            du[i]++;du[n+1]++;
            A.du[i]++;A.du[n+1]++;
            B.du[i]++;B.du[0]++;
            A.add(0,i);A.add(i,n+1);
            B.add(i,0);B.add(n+1,i);
        }
        A.solve(0);B.solve(n+1);
    
        for(int i=1;i<=m+2*n;++i)
            w[i]=A.dis[A.G[i].u]+B.dis[A.G[i].v]-1;
    
        h=t=1;qs[1]=0;
        mn=INF;
        while(h<=t)
        {
            int x=qs[h++];
            for(int i=B.head[x];i;i=B.G[i].nxt)
            dele(w[i]);
            if(x!=0 && x!=n+1)
            {
                int y=p.top();
                if(y<mn)
                    mn=y,ans=x;
                else if(mn==y)ans = min(ans, x);
            }
            for(int i=A.head[x];i;i=A.G[i].nxt)
            {
                int y=A.G[i].v;
                p.push(w[i]);
                du[y]--;
                if(!du[y])
                    qs[++t]=y;
            }
        }
        printf("%d %d
",ans,mn);    
    }

    

    return 0;
}