Summary: Depth-first Search(DFS)

There are generally two methods to write DFS algorithm, one is using recursion, another one is using stack. （reference from Wiki Pedia）

Pseudocode for both methods:

A recursive implementation of DFS:

procedure DFS(G,v):
      label v as discovered
      for all edges from v to w in G.adjacentEdges(v) do
          if vertex w is not labeled as discovered then
              recursively call DFS(G,w)

A non-recursive implementation of DFS(using stack):

  procedure DFS-iterative(G,v):
      let S be a stack
      S.push(v)
      while S is not empty
            v ← S.pop() 
            if v is not labeled as discovered:
                label v as discovered
                for all edges from v to w in G.adjacentEdges(v) do
                    S.push(w)

The non-recursive implementation is similar to breadth-first search but differs from it in two ways: it uses a stack instead of a queue, and it delays checking whether a vertex has been discovered until the vertex is popped from the stack rather than making this check before pushing the vertex.

Here's another good explenation: http://www.algolist.net/Algorithms/Graph/Undirected/Depth-first_search

Depth-first search, or DFS, is a way to traverse the graph. Initially it allows visiting vertices of the graph only, but there are hundreds of algorithms for graphs, which are based on DFS. Therefore, understanding the principles of depth-first search is quite important to move ahead into the graph theory. The principle of the algorithm is quite simple: to go forward (in depth) while there is such possibility, otherwise to backtrack.

Algorithm

In DFS, each vertex has three possible colors representing its state:

white: vertex is unvisited;

gray: vertex is in progress;

black: DFS has finished processing the vertex.

NB. For most algorithms boolean classification unvisited / visited is quite enough, but we show general case here.

Initially all vertices are white (unvisited). DFS starts in arbitrary vertex and runs as follows:

1. Mark vertex u as gray (visited).
2. For each edge (u, v), where u is white, run depth-first search for u recursively.
3. Mark vertex u as black and backtrack to the parent.

Example. Traverse a graph shown below, using DFS. Start from a vertex with number 1.

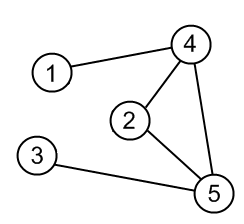	Source graph.
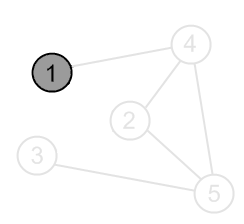	Mark a vertex 1 as gray.
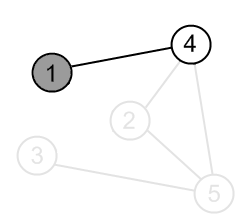	There is an edge (1, 4) and a vertex 4 is unvisited. Go there.
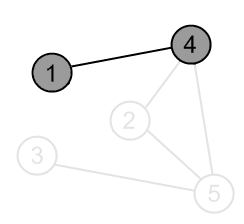	Mark the vertex 4 as gray.
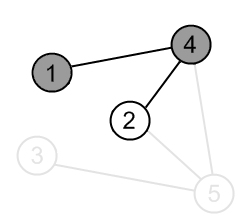	There is an edge (4, 2) and vertex a 2 is unvisited. Go there.
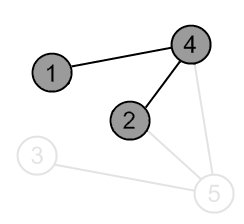	Mark the vertex 2 as gray.
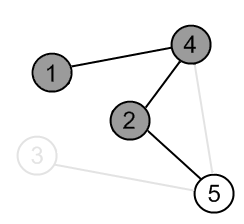	There is an edge (2, 5) and a vertex 5 is unvisited. Go there.
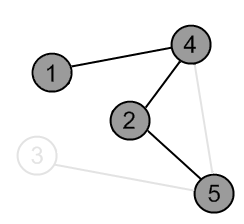	Mark the vertex 5 as gray.
	There is an edge (5, 3) and a vertex 3 is unvisited. Go there.
	Mark the vertex 3 as gray.
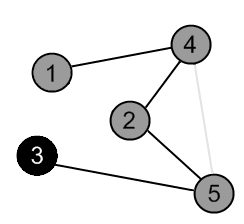	There are no ways to go from the vertex 3. Mark it as black and backtrack to the vertex 5.
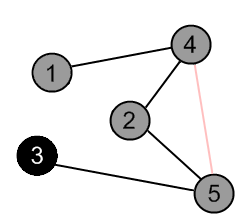	There is an edge (5, 4), but the vertex 4 is gray.
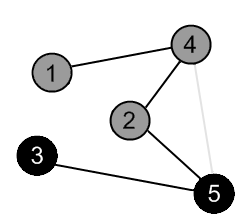	There are no ways to go from the vertex 5. Mark it as black and backtrack to the vertex 2.
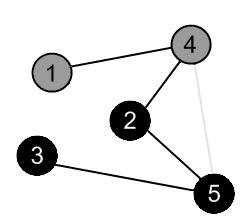	There are no more edges, adjacent to vertex 2. Mark it as black and backtrack to the vertex 4.
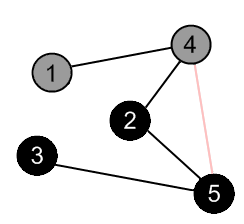	There is an edge (4, 5), but the vertex 5 is black.
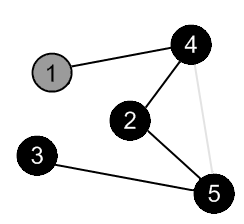	There are no more edges, adjacent to the vertex 4. Mark it as black and backtrack to the vertex 1.
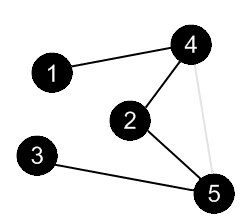	There are no more edges, adjacent to the vertex 1. Mark it as black. DFS is over.

Complexity analysisIf a graph is disconnected, DFS won't visit all of its vertices. For details, see finding connected components algorithm.As you can see from the example, DFS doesn't go through all edges. The vertices and edges, which depth-first search has visited is a tree. This tree contains all vertices of the graph (if it is connected) and is called graph spanning tree. This tree exactly corresponds to the recursive calls of DFS.

Assume that graph is connected. Depth-first search visits every vertex in the graph and checks every edge its edge. Therefore, DFS complexity is O(V + E). As it was mentioned before, if an adjacency matrix is used for a graph representation, then all edges, adjacent to a vertex can't be found efficiently, that results in O(V²)complexity. You can find strong proof of the DFS complexity issues in [1].

Java Implementation

public class Graph {
…    
     
enum VertexState {
          White, Gray, Black 
      }
     
      public void DFS()
      {
            VertexState state[] = new VertexState[vertexCount];
            for (int i = 0; i < vertexCount; i++)
                  state[i] = VertexState.White;
            runDFS(0, state);
      }
     
      public void runDFS(int u, VertexState[] state)
      {
            state[u] = VertexState.Gray;
            for (int v = 0; v < vertexCount; v++)
                  if (isEdge(u, v) && state[v] == VertexState.White)
                        runDFS(v, state);
            state[u] = VertexState.Black;
      }
}