学习日记(2.19 BP神经网络完整代码解读)

BP网络实现手写数字识别代码解读

1.添加偏置

#添加偏置
        temp=np.ones([X.shape[0],X.shape[1]+1])
        temp[:,0:-1]=X
        X=temp

np.ones()函数

numpy.ones()函数的功能是返回一个全都是1的N维数组，其中shape（用来指定返回数组的大小）、dtype（数组元素的类型）、order（是否以内存中的C或Fortran连续（行或列）顺序存储多维数据）。后两个参数都是可选的，一般只需设定第一个参数。

shape[]的功能是： 0查询行数，1查询列数

temp=np.ones([X.shape[0],X.shape[1]+1])
#在这里的作用就是先产生一个和X一样多行但是多一列的全部是1的数组
temp[:,0:-1]=X
#用X数组的值覆盖整个新数组的所有行，第一列到最后一列，最后一列依旧全是1
X=temp
#再把整个增加一列偏置的数组给数据集X，得到带有偏置的数据集

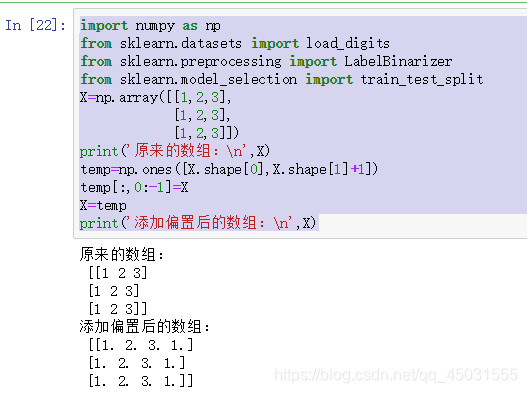
举一个小例子：

import numpy as np
from sklearn.datasets import load_digits
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split
X=np.array([[1,2,3],
            [1,2,3],
            [1,2,3]])#使用python中的数组使一定要先numpy.array
print('原来的数组：
',X)
temp=np.ones([X.shape[0],X.shape[1]+1])
temp[:,0:-1]=X
X=temp
print('添加偏置后的数组：
',X)

运行结果：

2.随机选取一个数据并将其转换为2维

i =np.random.randint(X.shape[0])#随机选取一个数据
            x=[X[i]]
            x=np.atleast_2d(x)#转为2维数据

函数解析：

numpy.random.randint(low, high=None, size=None, dtype='l')

用于产生随机数，随机数组
low: int
生成的数值最低要大于等于low。
（hign = None时，生成的数值要在[0, low)区间内）
high: int (可选)
如果使用这个值，则生成的数值在[low, high)区间。
size: int or tuple of ints(可选)
输出随机数的尺寸，比如size = (m * n* k)则输出同规模即m * n* k个随机数。默认是None的，仅仅返回满足要求的单一随机数。
dtype: dtype(可选)：
想要输出的格式。如int64、int等等

import numpy as np
from sklearn.datasets import load_digits
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split
i=np.random.randint(low=5,high=10,size=5)#产生一个在(5,10)之间的长度为5的一位数组
print('产生一个在(5,10)之间的长度为5的一位数组:
',i)
j=np.random.randint(low=5,high=10,size=(2,3))#产生一个在(5,10)之间的2行3列的数组
print('产生一个在(5,10)之间的2行3列的数组:
',j)

运行截图：

i =np.random.randint(X.shape[0])#随机选取一个数据
#X.shape[0]是这个数组的行数，我们在所有行中挑选出一行，i就是这一行的行数
            x=[X[i]]#用x保存行数
            x=np.atleast_2d(x)#转为2维数据
            #np.atleast_Xd转换为X维的数组
       

BP算法部分

            L1=sigomid(np.dot(x,self.V))#隐藏层的输出
            L2=sigomid(np.dot(L1,self.W))#输出层的输出
            
            L2_delta=(y[i]-L2)*dsigomid(L2)
            L1_delta=L2_delta.dot(self.W.T)*dsigomid(L1)
            
            self.W+=lr*L1.T.dot(L2_delta)
            self.V+=lr*x.T.dot(L1_delta)

下面的部分可能会涉及到我昨天的博客记录到的BP算法推导

函数 numpy.dot()

dot是用来计算矩阵乘法的，dot(x,y) 中 x是 mn的矩阵，y是nm的矩阵
配上图片公式可能会更有利于理解,因为这是在循环中，我就把第一轮的数学公式和代码匹配

L1=sigomid(np.dot(x,self.V))#隐藏层的输出

L2=sigomid(np.dot(L1,self.W))#输出层的输出

#根据delta学习规则求偏导数， （traget-真实值）X sigomid函数的导数 X 前面隐藏层∑和权值的偏导数 
L2_delta=(y[i]-L2)*dsigomid(L2)

L1_delta=L2_delta.dot(self.W.T)*dsigomid(L1)

第一行代码是：

第二行代码：


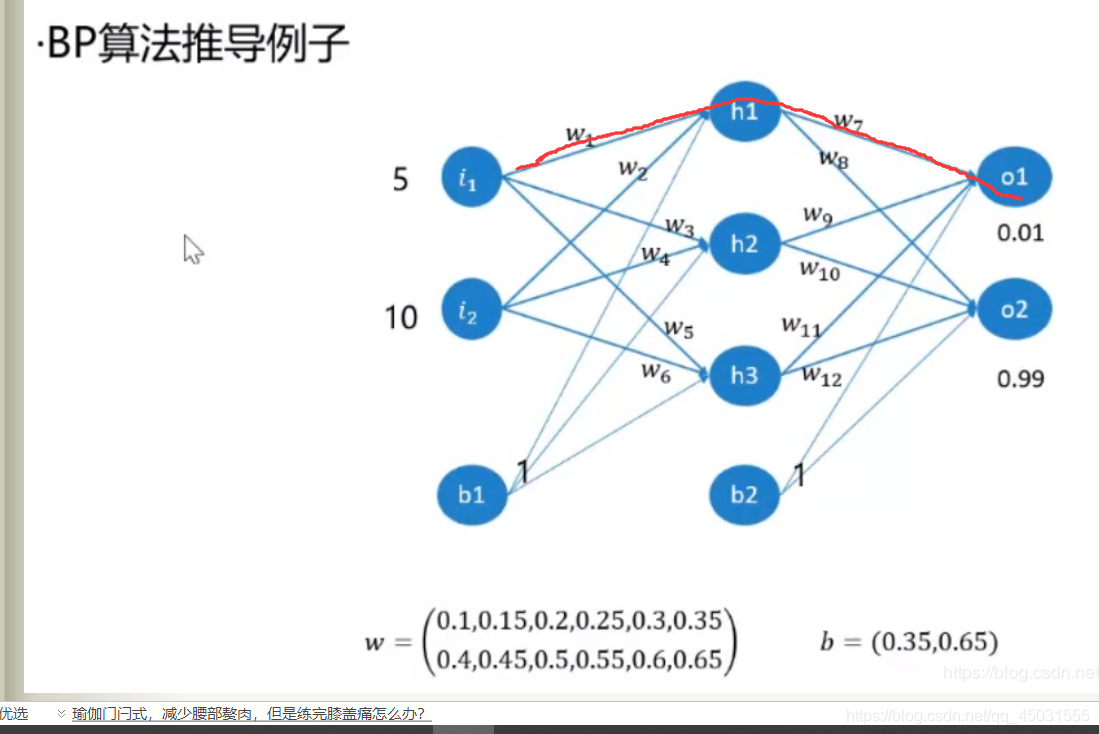
权重w1和权重w7的计算过程是有重复的故在算出W7 偏导后的数值依然可以参与计算到W1的delta，代码算法和公式推导并不是一一对应的，跟着感觉走是了。我们推导的时候，是先算出 △W7再 算△W1，并没有发现他们的偏导中是存在一定关系的，L2_delta.dot(self.W.T)就是把∑求和 net和out的关系。而dsigomid(L1)这又是求偏导的关系，算出来就是 关于输入层和隐藏层之间的w的delta。

#delta 算出来了就用来改变原来权重的数值，使之不断更新
self.W+=lr*L1.T.dot(L2_delta)
self.V+=lr*x.T.dot(L1_delta)

这里就很好理解了，只要能理解一轮做出的训练，就基本上理解了BP反向传播思想。

反馈训练状况：

#每训练1000次预测一次准确率
            if n%1000==0:
                predictions=[]
                for j in range(X_test.shape[0]):
                    o=self.predict(X_test[j])
                    predictions.append(np.argmax(o))#获取预测结果
                accuracy=np.mean(np.equal(predictions,y_test))
                print('epoch:',n,'accuracy:',accuracy)

函数解读：

numpy.argmax(array,axis=n)#返回n维的最大索引

numpy.mean()#对所有元素求平均值，可以算出精确度

numpy.equal()#判断两个数组是否相同

 def predict(self,x):
            temp=np.ones(x.shape[0]+1)
            temp[0:-1]=x
            x=temp
            x=np.atleast_2d(x)#转化为2维数据
            
            L1=sigomid(np.dot(x,self.V))#隐藏层输出
            L2=sigomid(np.dot(L1,self.W))#输出层输出
            return L2

用test测试集的数据来正向计算出输出层的数值，把这些数值放在一起和y_test做对比，反馈出当前模型的精确度。

BP神经网络识别手写数字

可能有的朋友很好奇数据集从哪里来的下面给大家展示一下：

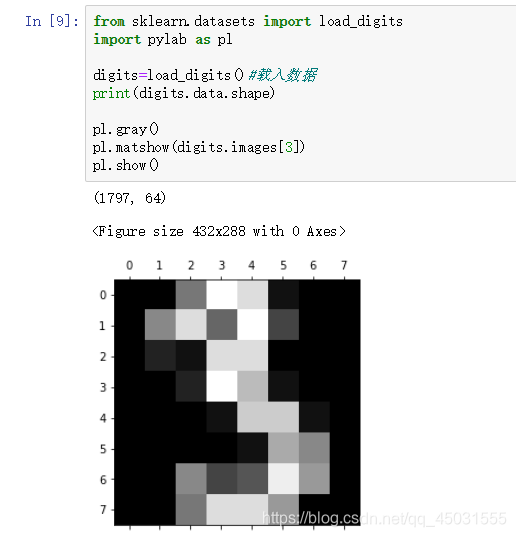
用灰度的二维(8X8)数组来写数字
下面是BP识别代码

import numpy as np
from sklearn.datasets import load_digits
from sklearn.preprocessing import LabelBinarizer
from sklearn.model_selection import train_test_split

def sigomid(x):
    return 1/(1+np.exp(-x))
def dsigomid(x):
    return x*(1-x)

class NeuralNetwork:
    def __init__(self,layers):#(64,100,10)
        #权值的初始化，范围-1到1
        self.V=np.random.random((layers[0]+1,layers[1]+1))*2-1
        self.W=np.random.random((layers[1]+1,layers[2]))*2-1
        
    def train(self,X,y,lr=0.11,epochs=10000):
        #添加偏置
        temp=np.ones([X.shape[0],X.shape[1]+1])
        temp[:,0:-1]=X
        X=temp
        
        for n in range(epochs+1):
            i =np.random.randint(X.shape[0])#随机选取一个数据
            x=[X[i]]
            x=np.atleast_2d(x)#转为2维数据
            
            L1=sigomid(np.dot(x,self.V))#隐藏层的输出
            L2=sigomid(np.dot(L1,self.W))#输出层的输出
            
            L2_delta=(y[i]-L2)*dsigomid(L2)
            L1_delta=L2_delta.dot(self.W.T)*dsigomid(L1)
            
            self.W+=lr*L1.T.dot(L2_delta)
            self.V+=lr*x.T.dot(L1_delta)
            
            #每训练1000次预测一次准确率
            if n%1000==0:
                predictions=[]
                for j in range(X_test.shape[0]):
                    o=self.predict(X_test[j])
                    predictions.append(np.argmax(o))#获取预测结果
                accuracy=np.mean(np.equal(predictions,y_test))
                print('epoch:',n,'accuracy:',accuracy)
                
    def predict(self,x):
            temp=np.ones(x.shape[0]+1)
            temp[0:-1]=x
            x=temp
            x=np.atleast_2d(x)#转化为2维数据
            
            L1=sigomid(np.dot(x,self.V))#隐藏层输出
            L2=sigomid(np.dot(L1,self.W))#输出层输出
            return L2
        
digits=load_digits()#载入数据
X=digits.data#数据
y=digits.target#标签
#输入数据归一化
X-=X.min()
X/=X.max()

nm=NeuralNetwork([64,100,10])#创建网络输入层是64，隐藏层是100，输出层是10
X_train,X_test,y_train,y_test=train_test_split(X,y)#这里不写其他参数默认的是1/4是测试数据，其他为训练
labels_train=LabelBinarizer().fit_transform(y_train)#标签二值化
labels_test=LabelBinarizer().fit_transform(y_test)#标签二值化

print('start~~')

nm.train(X_train,labels_train,epochs=20000)

print('end')

精确度情况：

百分之95左右的精确度，可以基本上完成手写数字的预测。

用sklearn库的神经网络实现识别

from sklearn.neural_network import MLPClassifier
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import classification_report,confusion_matrix
digits = load_digits()#载入数据
x_data = digits.data #数据
y_data = digits.target #标签

# 标准化
scaler = StandardScaler()
x_data = scaler.fit_transform(x_data)
x_train,x_test,y_train,y_test = train_test_split(x_data,y_data) #分割数据1/4为测试数据，3/4为训练数据
mlp = MLPClassifier(hidden_layer_sizes=(100,50) ,max_iter=500)
mlp.fit(x_train,y_train )
predictions = mlp.predict(x_test)
print(classification_report(y_test, predictions))
print(confusion_matrix(y_test,predictions))

引入混淆矩阵概念

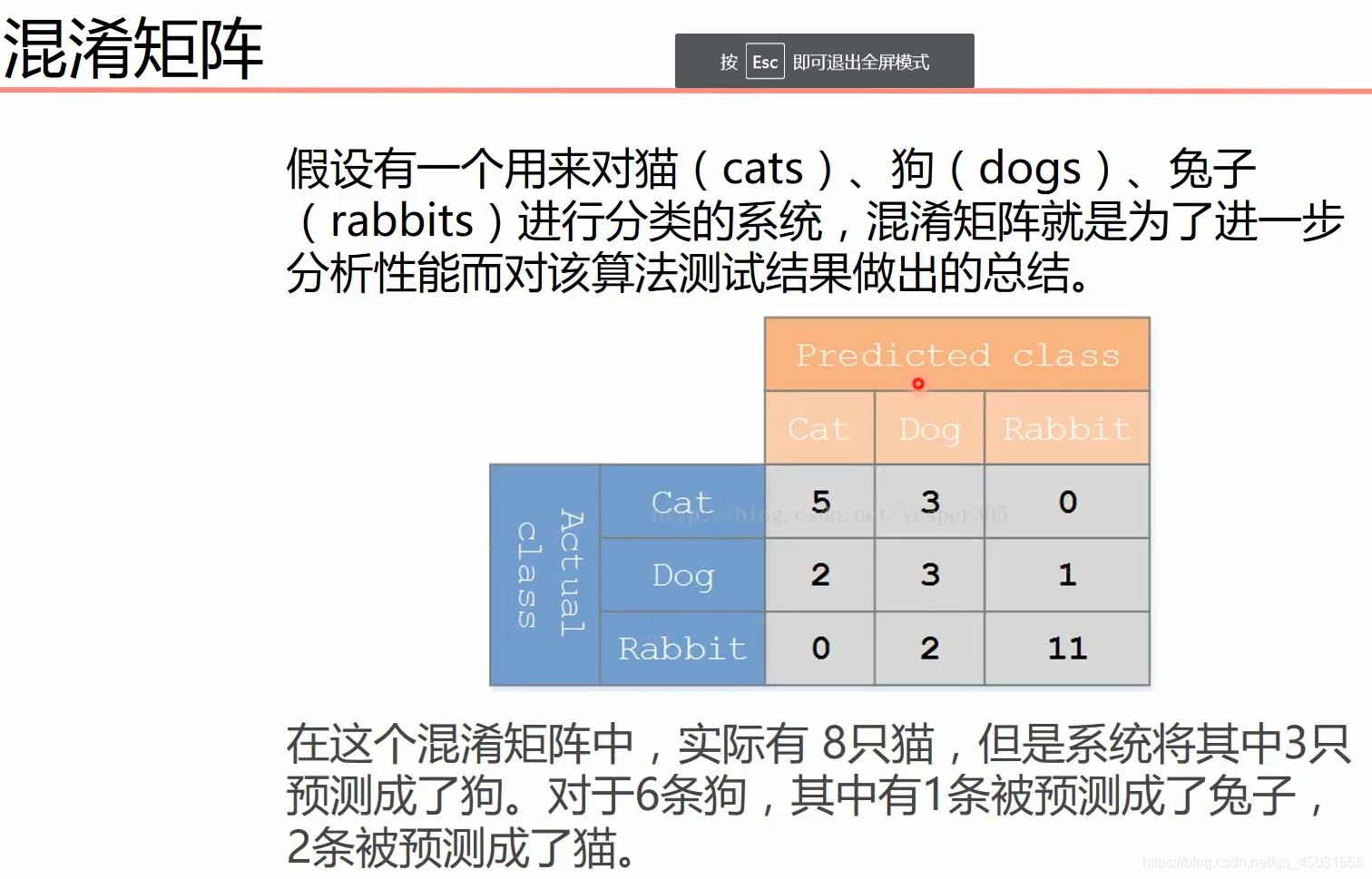
就像是一个坐标系，左边是真实值对应的标签，上面是目标值对应的标签，每一个坐标都代当前真实值被预测成当前目标值的个数
我们运行以上代码，打印出对应的混淆矩阵可以具体观察预测情况

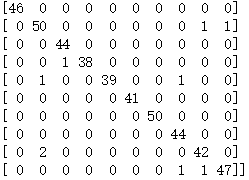
拿第2行举例，有50个1被预测成1，1个1被预测成8，1个1被预测成9
以上就是我个人通过看网课AI--MOOC
还有哔哩哔哩上的一些课程BP算法推导
这三天的博客第一天 对着教学视频敲代码，运行成功，获取一些数据处理，语法上的知识。
第二天：
自己看教学视频，在草稿纸上演算，跟着视频做，搞清楚变量关系，有了一点思路，慢慢理解了BP到底是怎么反向传播的。
第三天：
把代码和算法公式结合起来，解决了一些语法的问题，也解开了手写数字神秘的面纱