引言:
许多互联网公司在招聘前端开发人才时,不仅考察面试者对于前端知识的掌握程度,数据结构与算法也渐渐成为了默许的要求。
除了考察链表、二叉树、图等数据结构以外,在算法中最具有代表性的就是“手撕”快速排序算法。
快速排序算法,对于大多数人而言确实具有一定的难度。排序思路,代码设计以及难以理解的递归思想。
本文一步步带你写基于原生JavaScript语言的快速排序算法。
思想:
快速排序最核心的是分治思想,顾名思义,分而治之。
简单来说就是,按照一个标准(也称基准),将一个集合划分为多个集合,分开求解。
再通俗一点就是,将强大的敌军分成一块一块的,再逐个击破。
举个例子:

这个数组是乱序的。现在我们模拟快速排序的过程。
首先第一趟是这样的:
1.我们规定基准是当前数组第一个元素,也就是array[0]。
2.将当前数组遍历,比基准小的放left里,大的放right里。
3.一趟完成时,array会被划分为left、mid和right三部分。
如图所示:没有比mid小的元素,所以left数组里是空的;除mid外,其他比mid值大的元素全在right里。
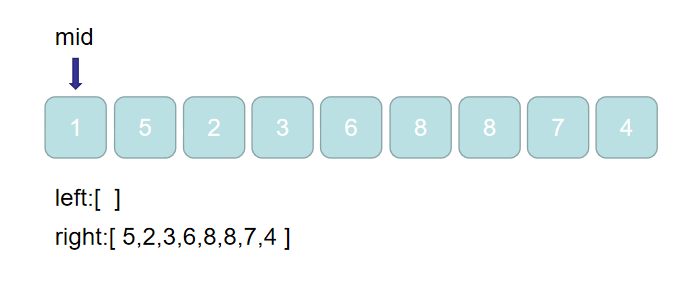
第二趟也是同样的道理:
1.对于left数组为空,则忽略。
2.对于right数组,里边的元素数量不止一个,那么就可以进行第二趟快排了:
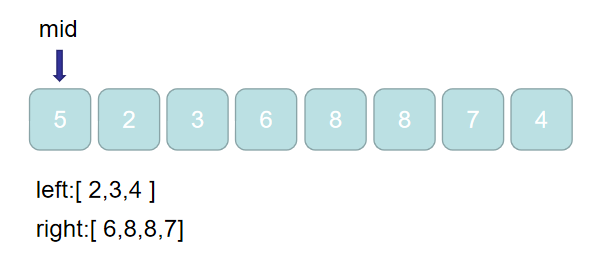
接着再对left和right分别进行划分,快排,宏观看来就是这样:
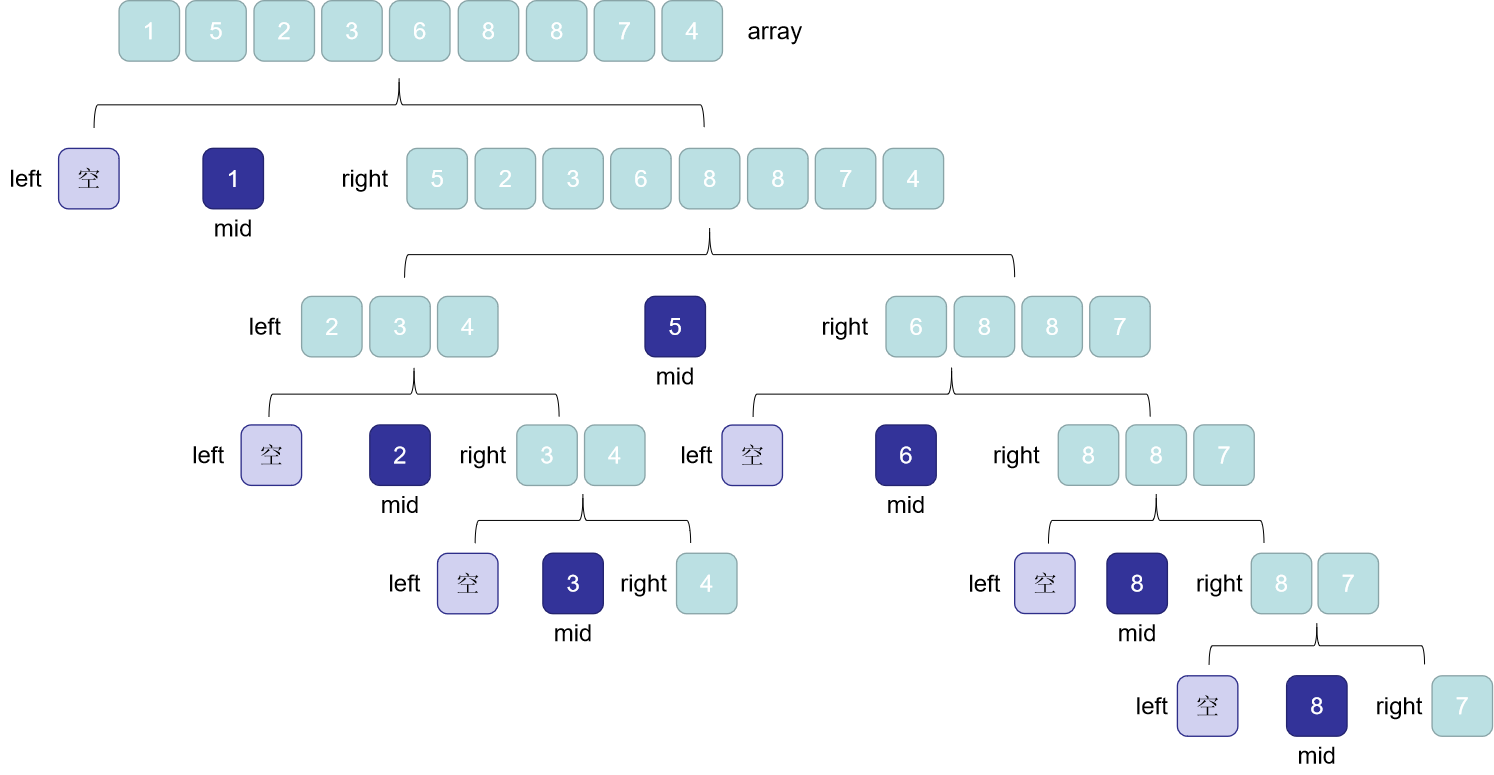
这种结构是不是非常熟悉,有点像二叉树呢?
设计与实现:
我们搞懂了过程,现在我们需要设计算法了。
在笔试中需要手撕快排,最好的办法就是尽量精简代码,写着也容易,看着也舒服!
根据前边我们看到的结构,是不是能够联想到二叉树的遍历呢?
二叉树遍历最精简的代码就是使用递归。(不管先序、中序还是后序)
说白了,递归就是在函数中调用自己,返回自己。
但最重要的还是要有个终止条件,也就是当数组中的元素数量不大于一个时,就没必要排序了。
无论怎样,先定义个quickSort方法:
function quickSort(arr) { if (arr.length <= 1) { return arr; } }
然后我们还需要定义数组left和right,还要将mid初始化为arr[0]。
function quickSort(arr) { if (arr.length <= 1) { return arr; } let left = []; let right = []; let mid = arr[0]; }
这时我们就要遍历数组了,从mid后边的元素开始。
若第i个元素比mid小,就放到left中。
若第i个元素比mid大或者一样大,就放到right中。
所以,上代码:
function quickSort(arr) { if (arr.length <= 1) { return arr; } let left = []; let right = []; let mid = arr[0]; for (let i = 1; i < arr.length; i++) { if (arr[i] < mid) { left.push(arr[i]); } else { right.push(arr[i]); } } }
这样,第一趟排序的结果就可以知道了,我们用js的concat方法将left、mid和right拼接一下。
function quickSort(arr) { if (arr.length <= 1) { return arr; } let left = []; let right = []; let mid = arr[0]; for (let i = 1; i < arr.length; i++) { if (arr[i] < mid) { left.push(arr[i]); } else { right.push(arr[i]); } } return left.concat(mid, right); }
我们运行一下,看结果:
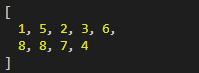
我们用流程推理一下,果然是第一趟排序的结果。
接下来,我们需要进行第二趟、第三趟……最后一趟排序。
这时我们就要用到递归思想了,我们需要对left和right再进行quickSort方法的调用。
那么显而易见,这么写就顺理成章了:
function quickSort(arr) { if (arr.length <= 1) { return arr; } let left = []; let right = []; let mid = arr[0]; for (let i = 1; i < arr.length; i++) { if (arr[i] < mid) { left.push(arr[i]); } else { right.push(arr[i]); } } return quickSort(left).concat(mid, quickSort(right)); }
好了,这个方法写完了,一切都是那么合理,我们调用一下看看结果:
console.log(quickSort([1, 5, 2, 3, 6, 8, 8, 7, 4]));
和想象中的一样,一切都在计划中:

至此,快速排序就写完了,至少在笔试中这么写足够用了!
分析:
对于快速排序,平均情况的时间复杂度为:O(n*lgn)。
当一个序列基本有序,就个别一个元素位置不对,那么也就是快速排序算法的最差情况,时间复杂度为:O(n*n)。
所以,与其他排序算法相比,快速排序的性价比还是最高的,因此使用也最广泛。