最优贸易
前言
一眼瞄到题面中的样例图示——图论!
再去读题,想到了最短路暴力求解,根据数据范围分析一下,拿(50pts)应该是没问题的(虽然暴力的时间复杂度真的大的可怕,大概是(O(n^3)))
所以,下面会介绍我的暴力最短路版实现以及正解版实现(正解之一:分层图)
暴力最短路
PS:大家可以直接跳到后面看分层图的讲解qwq
怎么用最短路来骗范围小的暴力分呢?
枚举呗!我们循环枚举每一种珂行的买入卖出方案,然后比较出其中的最大值即可
其中可行的方案必须满足以下规则(设每个点的价格为(c[i]),买入点为(i),卖出点为(j)):
-
路径必须是从起点(1)到终点(n)(其中可多次经过任意点)即:(1)和(i)必须连通,(i)和(j)必须连通,(j)和(n)必须连通
-
(c[j])必须(>)(c[i]),因为目的是赚钱,所以肯定低入高出啊!否则就不进行贸易了
满足以上条件后我们就可以将(c[j]-c[i])与(ans)作比较,最后输出保存了最大答案的(ans)即可(注意, (1)和(n)这两个点也可能作为买入点或卖出点)
这个思路还是很容易就编出代码的(Dijkstra和SPFA是一样的(50pts)):
#include <bits/stdc++.h>
using namespace std;
queue<int> q;
int n,m,x,y,z,tot,ans,c[500010];
int dis[5201][5201],vis[500010],head[500010];
struct node {
int to,net;
} e[500010];
inline void add(int u,int v) {
e[++tot].to=v;
e[tot].net=head[u];
head[u]=tot;
}
inline void spfa(int s) {
for(register int i=1;i<=n;i++) {
vis[i]=0;
dis[s][i]=20050206;
}
dis[s][s]=0;
vis[s]=1;
q.push(s);
while(!q.empty()) {
int x=q.front();
q.pop();
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(dis[s][v]>dis[s][x]+1) {
dis[s][v]=dis[s][x]+1;
if(!vis[v]) {
vis[v]=1;
q.push(v);
}
}
}
}
}
int main() {
scanf("%d%d",&n,&m);
for(register int i=1;i<=n;i++) {
scanf("%d",&c[i]);
}
for(register int i=1;i<=m;i++) {
scanf("%d%d%d",&x,&y,&z);
add(x,y);
if(z==2) add(y,x);
}
for(register int i=1;i<=n;i++) {
spfa(i);
}
for(register int i=1;i<=n;i++) {
for(register int j=1;j<=n;j++) {
if(dis[j][n]==20050206) continue;
if(c[j]-c[i]<=ans||c[j]<=c[i]) continue;
if(dis[1][i]!=20050206&&dis[i][j]!=20050206) {
ans=c[j]-c[i];
}
}
}
printf("%d",ans);
return 0;
}
分层图(正解之一)
这题还能分层图??!!
在看到了这篇题解的标题后,简直是顿悟啊!如果对分层图比较熟悉,题意转换能力较好的OIer应该还是想得出来(跟我没啥关系...)
不了解分层图为何物的,可以看我的这篇题解 (虽然讲的是分层图最短路,但是也可以辅助了解分层图qvq)
- 来解释一下为什么会想到分层图
题目中明确表示贸易只会进行一次!
那我们将买入标记为第一层与第二层连边,边权为(-c[i]);将卖出标记为第二层与第三层连边,边权为(c[i])。然后从起点(1)走到(3*n)的最长路就是我们最终的答案!
(有点不好理解?那我们来看看图,这图有点大..不好意思啊)
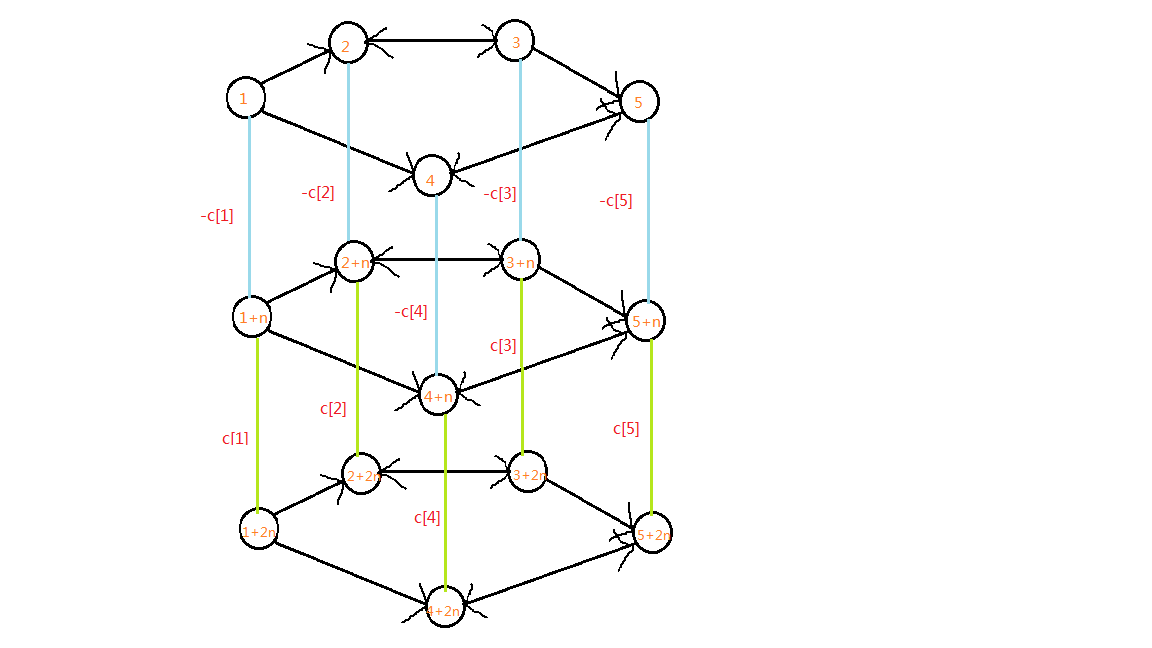
蓝色的线表示的就是买入,绿色的线表示的就是卖出,旁边的东西就是边权
在每一层中,有边相连的两个点的边权为0就好,这样不会影响结果
现在给出(100pts)的AC代码qwq:
#include <bits/stdc++.h>
using namespace std;
int n,m,u,v,z,tot,c[300010];
int dis[300010],head[300010];
priority_queue<pair<int,int> > q;
struct node {
int to,net,val;
} e[300010];
inline void add(int u,int v,int w) {
e[++tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
inline void dijkstra() {
for(register int i=1;i<=3*n;i++) dis[i]=-20050206; //注意是3*n而不只是n!
dis[1]=0;
q.push(make_pair(0,1));
while(!q.empty()) {
int x=q.top().second;
int y=q.top().first;
q.pop();
if(dis[x]>y) continue;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(dis[v]<dis[x]+e[i].val) { //取最长路
dis[v]=dis[x]+e[i].val;
q.push(make_pair(dis[v],v));
}
}
}
}
int main() {
scanf("%d%d",&n,&m);
for(register int i=1;i<=n;i++) scanf("%d",&c[i]);
for(register int i=1;i<=m;i++) { //每一层中连边
scanf("%d%d%d",&u,&v,&z);
add(u,v,0);
add(u+n,v+n,0);
add(u+n+n,v+n+n,0);
if(z==2) { //双向边
add(v,u,0);
add(v+n,u+n,0);
add(v+n+n,u+n+n,0);
}
}
for(register int i=1;i<=n;i++) { //层与层之间连边
add(i,i+n,-c[i]);
add(i+n,i+n+n,c[i]);
}
dijkstra();
printf("%d",max(0,dis[3*n]));
return 0;
}
最后,如果有任何不懂或不对的地方,欢迎大家在底下留言,我会及时回复,谢谢orz