双调路径
前言
可能是我语文不太好,题目没读懂,感谢同桌帮助我理清题意
题意
对着图讲吧:
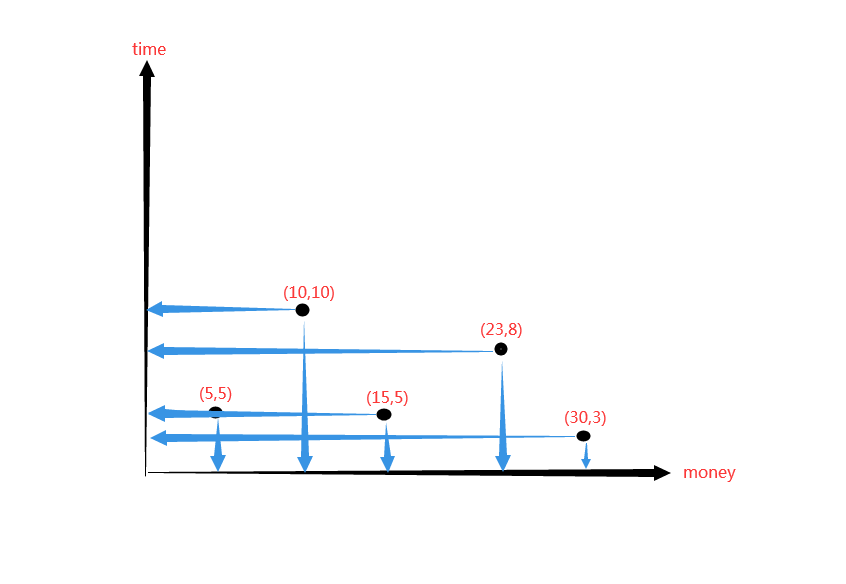
如图,横轴表示花费的金钱,纵轴表示花费的时间,点表示一条路径
-
点((5,5))和点((30,3))是优秀点
-
点((10,10))、点((15,5))和点((23,8))是无用点
来解释一下:
-
点((5,5))明显比点((15,5))优秀,因为花费同样时间,花费金钱少的优秀
-
点((10,10))和点((23,8))则肯定是无用点,因为它们花费的时间和金钱都多
-
点((5,5))和点((30,3))都是优秀点,因为一个花费的金钱少,一个花费的时间少(相当于不同维度)
推广为一般性问题:
设我们当前的路径表示为((x,y)),下一条路径表示为((u,v))
-
如果 (u) 比 (x) 小但 (v) 比 (y) 大,那么两条路都暂为优秀
-
如果 (u) 比 (x) 大但 (v) 比 (y) 小,那么两条路都暂为优秀
-
如果 (u) 比 (x) 小且 (v) 比 (y) 小,那么((u,v))暂为优秀,而((x,y))一定为无用点
分析
题目要求求出从 (s) 到 (e) 的最小路径条数
理解了题意,那么应该很容易就能想出双限制的最短路做法吧(别在意名字...)
什么意思?
普通最短路就是距离限制,我们通过 (dis[x]) 表示到达点 (x) 的最小距离
本题最短路则是限制距离(时间)和花费,那我们就加一维嘛!
—— 用 (dis[x][y]) 表示到达点 (x) 花费 (y) 块钱的最小距离(时间)
最后枚举花费 (i) ,然后找到优秀点 (dis[e][i]),有多少优秀点答案就是多少
怎么判断是否是优秀点?
设一个变量 (ans) (=) (2005020600)(极大值就可以) ,如果当前的 (dis[e][i]) (<) (ans) ,则是优秀点( (ans) 表示的是时间)
代码
感觉上面讲的还是挺清楚了qwq,现在贴出代码:
PS:没加树状数组优化什么的,跑得确实有点慢,(1s+)
#include <bits/stdc++.h>
using namespace std;
queue<pair<int,int> > q;
int n,m,s,E,p,r,c,t,tot,sum,ans=2005020600,maxn;
int dis[101][30001],vis[101][3001],head[520010];
struct node {
int to,ti,val,net;
} e[520010];
inline void add(int u,int v,int w,int tim) {
e[++tot].ti=tim;
e[tot].to=v;
e[tot].val=w;
e[tot].net=head[u];
head[u]=tot;
}
inline void spfa(int s) { //其实就是板子
for(register int i=1;i<=n;i++) {
for(register int j=0;j<=maxn;j++) {
dis[i][j]=2005020600;
}
}
dis[s][0]=0; //到达点s花费0的最短时间为0
vis[s][0]=1;
q.push(make_pair(s,0)); //为了不开两个queue,我选择开pair
while(!q.empty()) {
int x=q.front().first;
int y=q.front().second;
q.pop();
vis[x][y]=0;
for(register int i=head[x];i;i=e[i].net) {
int v=e[i].to;
if(dis[v][y+e[i].val]>dis[x][y]+e[i].ti) {
dis[v][y+e[i].val]=dis[x][y]+e[i].ti;
if(!vis[v][y+e[i].val]) {
vis[v][y+e[i].val]=1;
q.push(make_pair(v,y+e[i].val)); //注意第二个存的是花费还不是dis[v][y+e[i].val]!
}
}
}
}
}
int main() {
scanf("%d%d%d%d",&n,&m,&s,&E);
for(register int i=1;i<=m;i++) {
scanf("%d%d%d%d",&p,&r,&c,&t);
add(p,r,c,t);
add(r,p,c,t);
maxn+=c; //maxn表示最多的花费上限
}
spfa(s);
for(register int i=0;i<=maxn;i++) { //枚举花费找答案
if(dis[E][i]<ans) {
sum++;
ans=dis[E][i];
}
}
printf("%d",sum);
return 0;
}
最后,如果这篇题解有任何问题或不懂的地方,欢迎下方留言区评论,我会及时回复、改正,谢谢大家啊orz