[JSOI2013]侦探 JYY

P5954 [JSOI2013]侦探 JYY

说明

2020.9.14的考试题

考场上没想出来，之后借鉴了学长的思路才改正。

---

思路

设给出的已知事件为 (x)

• 朴素想法

对于每个 (x)，显然所有子孙是要选的，那么我们就只需要考虑祖先怎么选。

首先任选一个父亲往上走直到走到一个入度为0的点 (top)，然后再从 (top) 往下标记所有点（这些点就全部都要输出）

如果此时还存在一个入度为0且没被标记过的点能够走到 (x)，则说明 (x) 的父亲相互矛盾，即样例二的情况，那么所有的父亲都不能选

但是，这样做就会遗漏掉一种情况，而且大概率会 (T) 掉

• 完整思路

来看样例四，我们会发现：即使 (x=3) 的父亲相互矛盾，但是输出却不止3，而还有4

这样我们的朴素算法就被 (Hack) 掉了，看一下图：

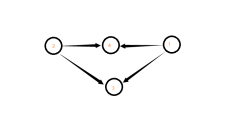
归纳一下，样例四的情况即：即使当前 (x) 的所有父亲不能选，但是所有父亲有除 (x) 以外的公共儿子（例如点4），那么这些公共儿子也一定会被选

这种情况怎么处理？

设当前已经确定要输出的数的个数为 (sum)

我们首先将每个点的所有祖先存入对应的 (set) 中，然后对于每个不是 (x) 的点 (i) 进行一次 (check)，判断所有不在 (i) 的路径上的点中已经被确定的数的个数 (cnt) 是否等于 (sum)

如果小于 (sum)，则说明当前点 (i) 一定会被选中输出。因为剩余的被确定的数（即 (sum-cnt)）只可能存在于当前点 (i) 所在的路径上，那么 (i) 一定会被选中

(check) 算法框架：

1. 找到除当前点 (i) 的父节点以外的入度为0的点

2. 然后遍历找到的这些点的子孙

3. 所有以上找到的点就是不存在于当前点 (i) 路径上的点

有一点抽象，来看一个例子：

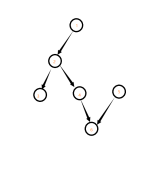
则有：

set[1]={1}
set[2]={1,2}
set[3]={1,2,3}
set[4]={1,2,4}
set[5]={5}
set[6]={1,2,4,6}

假设当前点 (i=2)，那么 ({5，6}) 就是找到的不存在于 (i) 的路径上的点

---

代码

如果思路有些不懂也不要急，结合下面的代码理解，多画一下样例，就好了qwq

#include <bits/stdc++.h>
using namespace std;
set<int> fa[20010];
int d,m,n,x,y,tot,sum;
int in[20010],vis[20010],head[200010],viss[20010];

struct node {
	int to,net;	
} e[200010];

void add(int u,int v) {
	e[++tot].to=v;
	e[tot].net=head[u];
	head[u]=tot;
}

void bfs1(int now) {
	queue<int> q;
	memset(viss,0,sizeof(viss));
	q.push(now);
	viss[now]=1;
	while(!q.empty()) {
		int xx=q.front();
		q.pop();
		fa[xx].insert(now);
		for(int i=head[xx];i;i=e[i].net) {
			int v=e[i].to;
			if(viss[v]) continue;
			q.push(v);
			viss[v]=1;
		}
	}
}

int check(int now) {
	queue<int> q;
	memset(viss,0,sizeof(viss));
	for(int i=1;i<=d;i++) {
		if(fa[now].find(i)==fa[now].end()&&!in[i]) q.push(i),viss[i]=1;  //除x的父节点以外入度为0的节点（即不在x的路径上） 
	}
	int cnt=0;
	while(!q.empty()) {
		int xx=q.front();
		q.pop();
		cnt+=vis[xx];  //统计其中被确定的数的个数 
		for(int i=head[xx];i;i=e[i].net) {
			int v=e[i].to;
			if(viss[v]) continue;
			viss[v]=1;
			q.push(v);
		}
	}
	return cnt;
}

void bfs2() {
	queue<int> q;
	for(int i=1;i<=d;i++) {
		if(vis[i]) q.push(i);
	}
	while(!q.empty()) {
		int xx=q.front();
		q.pop();
		for(int i=head[xx];i;i=e[i].net) {
			int v=e[i].to;
			if(vis[v]) continue;
			vis[v]=1;
			q.push(v);
		}
	}
}

int main() {
	scanf("%d%d%d",&d,&m,&n);
	for(int i=1;i<=m;i++) {
		scanf("%d%d",&x,&y);
		add(x,y);
		in[y]++;
	}
	for(int i=1;i<=n;i++) {
		scanf("%d",&x); 
		vis[x]=1;  //所有被确定的事件不用管 
		sum++;  //sum表示已经被确定的事件个数 
	}
	for(int i=1;i<=d;i++) bfs1(i);   //找到每个点i的所有祖先 
	for(int i=1;i<=d;i++) {
		if(vis[i]) continue;
		if(check(i)<sum) {  //如果不在i的路径上的点中被确定的数的个数小于sum，则说明当前i一定会被选 
			vis[i]=1;
			sum++;
		}
	}
	bfs2();   //最后遍历标记所有能被确定的数，输出 
	for(int i=1;i<=d;i++) {
		if(vis[i]) printf("%d ",i);
	}
	return 0;
}

---