题目描述
给出一个n个点,m条边的无向图,求图的割点。
关于割点
在无向连通图中,如果将其中一个点以及所有连接该点的边去掉,图就不再连通,那么这个点就叫做割点(cut vertex / articulation point)。
题解
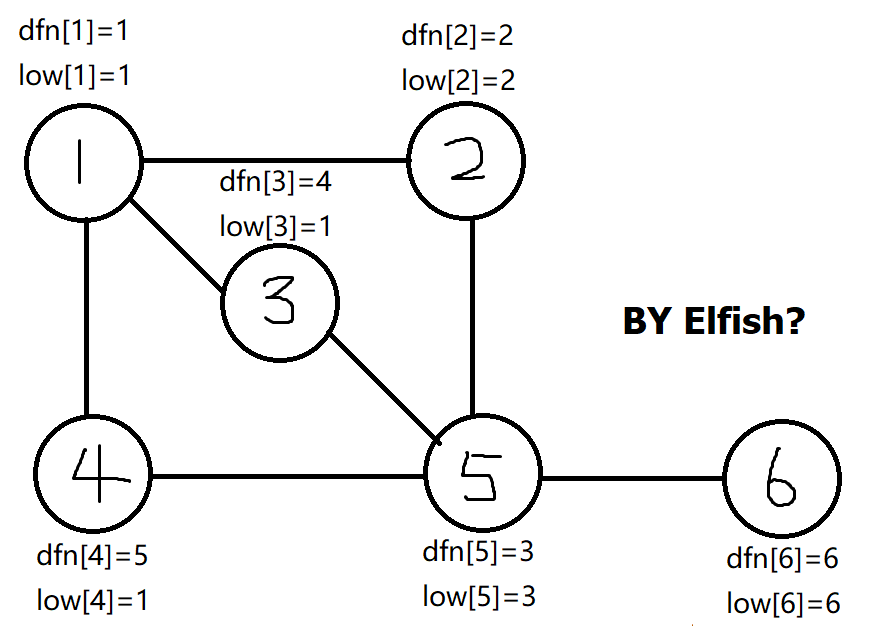
在一个无向图里的割点分为两种,第一种就是一棵树的根节点并且他的度要大于等于2,删去这个点他的子树就不连通了(如上图的1号点)。
第二种就要用到tarjan算法的思想,tarjan求出每个点的dfs顺序,然后记录他子树中能访问到的dfn最早的点。如果一个点不为根且他的子树的low大于他的dfn,即他的子树要在访问过他之后才能访问那个点,那么这个点删去以后图也会不连通。(如上图中的5,6号点必须在访问5之后才能访问到)。
代码
//洛谷3388 割点 tarjan #include<iostream> #include<cstdio> #include<algorithm> #include<cstring> using namespace std; int n,m,cnt,head[100005]; int dfn[100005],low[100005],cut[100005]; struct edge{ int next,to; }e[200005]; void insert(int u,int v){ cnt++; e[cnt].next=head[u];e[cnt].to=v; head[u]=cnt; } int top,ind,k; void tarjan(int x,int root){ dfn[x]=low[x]=++ind; int du=0; for(int i=head[x];i;i=e[i].next){ int s=e[i].to; if(!dfn[s]){ tarjan(s,root); low[x]=min(low[s],low[x]); if(low[s]>=dfn[x]&&x!=root)cut[x]=1; if(x==root)du++; } low[x]=min(dfn[s],low[x]); } if(x==root&&du>=2)cut[root]=1; } int mx=0; int ans; int main(){ scanf("%d%d",&n,&m); int u,v,t; for(int i=1;i<=m;i++){ scanf("%d%d",&u,&v); insert(u,v); insert(v,u); } for(int i=1;i<=n;i++){ if(!dfn[i])tarjan(i,i); } for(int i=1;i<=n;i++){ if(cut[i])mx++; } printf("%d ",mx); for(int i=1;i<=n;i++){ if(cut[i]){ printf("%d ",i); } } return 0; }