普通莫队

n个数，区间查询[L,R]出现了几种数字

时间复杂度(O(nsqrt n))

莫队的基本操作就是把n个数进行分块，每一块有(sqrt n)个，有(sqrt n)块，然后离线查询，把查询进行排序，按照分块位置排序，如果在同一个分块，那么就按照右区间排序，然后对于每一个排序进行暴力遍历即可
我们开一个数组cnt[i]，记录i出现的次数。显然，我们如果已经得到了[l, r]的cnt数组，我们可以O(1)得到[l, r + 1]、[l, r - 1]、[l + 1, r]、[l - 1, r]的cnt数组，只需要将变化的数++或--就可以了。所以莫队题思考在于如何维护add和del

算法

1.先进行分块，每块有分成(sqrt n)个,bein[j] = i表示第j个数属于第i个分块

for(int i = 1; i <= ceil((double)n/sqrt(n)); i++)
    for(int j = (i - 1) * sqrt(n) + 1; j <= i * sqrt(n); j++)
        bein[j] = i;

2.把查询进行离线并排序

struct Query{
    int l, r, id;
}q[maxn];

方法1：先按照查询区域的左区间所处的分块大小排序，如果位与同一个分块，那么久按照右区间排序

bool cmp(Query a,Query b){
    return bein[a.l] == bein[b.l] ? a.r < b.r : bein[a.l] < bein[b.l];
}

方法2：

bool cmp1(Query a, Query b) {
    return (bein[a.l] ^ bein[b.l]) ? bein[a.l] < bein[b.l] : ((bein[a.l] & 1) ? a.r < b.r : a.r > b.r);
}

for(int i = 1; i <= m; i++){
    scanf("%d%d", &q[i].l, &q[i].r);
    q[i].id = i;
}
sort(q + 1, q + m + 1, cmp1);

3.移动左右指针

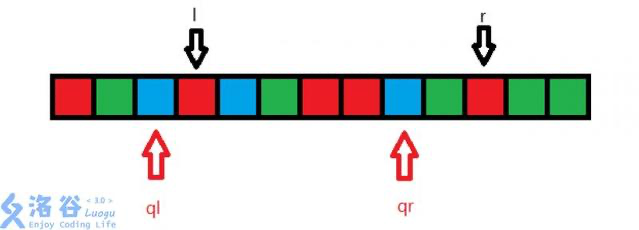
首先定义l为左指针，r为右指针,

左指针要初始化为1，右指针初始化为0，如果l = 0，那么先l++,a[1]统计1次，r++，a[1]又被统计1次

对于排序后的每一个查询

while(l < q[i].l)del(l++);//l右移
while(l > q[i].l)add(--l);//l左移
while(r < q[i].r)add(++r);//r右移
while(r > q[i].r)del(r--);//r左移

其中now表示当前查询区域不同数值的个数

void add(int x){//加入操作
    if(cnt[a[x]] == 0) now++;//如果a[x]这个数在之前没有出现过，
    ++cnt[a[x]];//这个数出现了一次
}

void del(int x){//删除操作
    --cnt[a[x]];
    if(cnt[a[x]] == 0) --now;//在这次操作后，[l,r]里，a[x]这个数没出现过了
}

那么

ans[q[i].id] = now;//当前查询区间的值就是now了

4.输出

for(int i = 1; i <= m; i++)
    printf("%d
", ans[i]);

关于时间复杂度

在while里面右指针是递增的，所以一个分块每次最多(O(n)),(sqrt n)个分块就是(O(nsqrt n))

在while里面左指针每个查询都在一个分块里移动为(sqrt n)，m个查询就是(O(msqrt n))

进行分块(O(n))

输入数据(O(n))

离线查询(O(mlogm))

所以是(O(nsqrt n))

注意

莫队是一个离线算法，不支持在线操作带修改

#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int maxn = 1e6 + 5;
int cnt[maxn],a[maxn];//cnt[i]表示数字i出现的次数，a[]是输入的数
int l = 1,r,now;//l是左指针,r是右指针,now是不同数字的个数
int bein[maxn],ans[maxn];//bein[]分块
void add(int x){//加入操作,右移
    if(cnt[a[x]] == 0)++now;
    ++cnt[a[x]];
}
void del(int x){//删除操作，左移
    --cnt[a[x]];
    if(cnt[a[x]] == 0)--now;
}
struct Query{
    int l,r,id;
}q[maxn];
bool cmp(Query a,Query b){
    return bein[a.l] == bein[b.l] ? a.r < b.r : bein[a.l] < bein[b.l];
}
int cmp1(Query a, Query b) {
    return (bein[a.l] ^ bein[b.l]) ? bein[a.l] < bein[b.l] : ((bein[a.l] & 1) ? a.r < b.r : a.r > b.r);
}
int main(){
    int n;
    scanf("%d",&n);
    for(int i = 1; i <= ceil((double)n / sqrt(n)); i++)
        for(int j = (i - 1) * sqrt(n) + 1; j <= i * sqrt(n); j++)
            bein[j] = i;
    for(int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    int m;
    scanf("%d",&m);
    for(int i = 1; i <= m; i++){
        scanf("%d%d", &q[i].l, &q[i].r);
        q[i].id = i;
    }
    sort(q + 1, q + m + 1, cmp1);

    for(int i = 1; i <= m; i++){
        while(l < q[i].l)del(l++);//l右移
        while(l > q[i].l)add(--l);//l左移
        while(r < q[i].r)add(++r);//r右移
        while(r > q[i].r)del(r--);//r左移
        ans[q[i].id] = now;
    }
    for(int i = 1; i <= m; i++){
        printf("%d
", ans[i]);
    }
    return 0;
}

题

统计(sum_{i=1}^{k}c_i^2)

传送门

其中(c_i)表示数字i在([l,r])中出现的次数，k是最大值

cnt[i]记录i出现的次数，那么

如果cnt[a[i]]++, ((x + 1)^2 = x^2+2x + 1)也就是now = now + 2 * cnt[a[i]] + 1

如果cnt[a[i]]--，((x - 1 )^2 =x ^2 -2x + 1)也就是now = now - 2 *cnt[a[i]] + 1

因为是统计出现次数，所以不需要判断是否出现过

void add(int x){
    now += (cnt[a[x]] << 1) + 1;
    cnt[a[x]]++;
}
void del(int x){
    now -= (cnt[a[x]] << 1) - 1;
    cnt[a[x]]--;
}

统计(sum_{i=1}^kC_{x_i}^2)

传送门

设区间[L,R] 总排列方式为(C_n^2 = frac{n*(n-1)}{2})

设(x_i)表示在该区间(i)出现的次数那么符合情况的排列方式有(sum_{i = 1}^k C_{x_i}^2 = frac{x_i * (x_ - 1)}{2})

对于增加1个数(C_{x+1}^2 = frac{x*(x + 1)}{2} = frac{x * (x-1)}{2} + x = C_x^2 + x)

对于减去1个数(C_{x-1}^2 = frac{(x -1)(x-2)}{2} = frac{x*(x-1)}{2} - (x-1) = C_x^2 -(x - 1))

查询区间异或和为k的个数

传送门

求[l,r]里异或和为k的个数，

• a[x]记录的是异或前缀和，因为是前缀和，所以([L,R])的异或和为$a[L-1] xor a[R] $ ，也就意味着

  while (l < q[i].l) { del(l - 1); ++l; }
  while (l > q[i].l) { l--, add(l - 1); } 
  

• cnt[i]还在存数i出现的次数

• $a xor b = c (等价于)a xor c = b$

• 如果要求出异或和为k的个数，只需把now加上cnt[a[x] ^ k]即可因为a[x] ^ z = k,那么我们只需要知道，值为z的有多少个即可

对于这题，牛客有一道题，给出一个数列a，求出异或值为0的不同字段数量

因为最大值是(2^{30} -1),而且只查询一次，所以不能用莫队

#include <iostream>
#include <map>
#define ll long long
using namespace std;
const int maxn = 2e5 + 5;
std::map<ll, ll> mp;
ll a[maxn],b[maxn];
int main(){
    int n;
    cin >> n;
    ll ans = 0;
    for(int i = 1; i <= n; i++){
        cin >> a[i];
        b[i] = a[i] ^ b[i - 1];
        if(b[i] == 0)ans++;//[1,i]异或和为0
        ans += mp[b[i]];//[l,i]异或和为0，l≠1
        mp[b[i]]++;
    }
    cout << ans << endl;
    return 0;
}