P1593 因子和

传送门
首先，求因子和，想到公式,用唯一分解定理求约数和

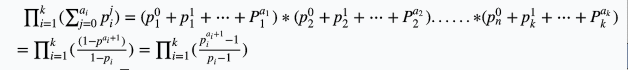
然后对于(a^b)看成b个上面的a相乘，然后所有的(p_i)一直加到(p_i^{b*a_i})即可
注意的一个地方在于，模很小，也就是说，在求逆元时要注意一下。

逆元存在的条件是a不是p的倍数，才存在inv(a,p)

那么如果说我求得的(p_i - 1)是mod的倍数，那么需要直接化简

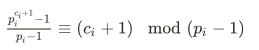
#include <iostream>
#include <cstdio>
#define ll long long
using namespace std;
const int mod = 9901;
const int N = 30;
ll pr[N], cou[N], tot = 0;
ll a, b;
void cal(int n){
    for(int i = 2; i * i <= n; i++){
        if(n % i == 0){
            pr[++tot] = i;
            while(n % i == 0) n /= i, cou[tot]++;
            cou[tot] *= b; 
        }
    }
    if(n > 1) pr[++tot] = n, cou[tot] = b; 
}
ll pow(ll a, ll b, ll p){
    ll ans = 1; a %= p;
    while(b){
        if(b & 1) ans = ans * a % p;
        a = a * a % p;
        b >>= 1;
    }
    return ans;
}
ll inv(ll a, ll p){
    return pow(a, p - 2, p); 
}
int main(){
    cin >> a >> b;
    cal(a);
    ll ans = 1;
    for(int i = 1; i <= tot; i++){
        if(pr[i] % mod == 1) {
            ans = ans * (cou[i] + 1) % mod;
            continue;
        }
        ll now = (pow(pr[i], cou[i] + 1, mod) - 1 + mod) % mod;
        now = now * inv(pr[i] - 1, mod) % mod;
        ans = ans * now % mod;
    }
    printf("%lld
", (ans + mod) % mod);
    return 0;
}