看懂题意的请直接跳过下一坨! 本人有表达障碍!
==========================================
题意: (题意真的很难很难懂啊!!! 去他娘的**)
有一个王国,王国里有一个国王(编号为1),他有(编号为2~n) n-1个臣子(这些臣子并不全和他有直接关系)
然后呢 国王要去打架,但是只有当他的x%个及以上的直系下属(与他有直接关系的臣子)做好打架的准备了,他才能去打架
他的直系下属也有下属,也要其中x%及以上的下属做好打架准备了,那些直系下属才会开始准备打架...直到最后一层下属(也就是没有下属的那些人)他们会直接开始准备打架
当然 (除了国王)所有臣子准备打架都需要时间$t_i$;
有一个上限时间T 臣子们准备的总时间不能超过T
给的是n(包括国王 共n个人(国王加臣子)),T
接下来是编号2~n的臣子们的信息(1号是国王) $p_i$和$t_i$
$p_i$代表该臣子是 编号为pi的人 的下属
$t_i$代表该臣子 准备打架需要的时间
问的是: 不超过T的情况下,准备战斗的臣子要尽量多,求x的最大值
是不是看了这么大一坨还是不知道讲什么...
那么我们来看个案例:
6 3 1 2 2 2 2 1 1 2 1 4
n=6 T=3 就是1个国王 5个臣子 臣子们要在3单位时间内准备好打架
接着
2号:1 2 3号:2 2 4号:2 1 5号:1 2 6号:1 4
他们的关系图是这样的:
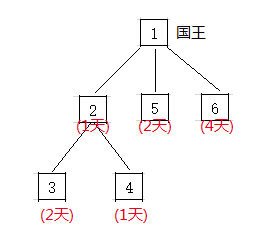
这些人中 3、4、5、6都是没有下属的 因此都可以直接开始准备打架
如果x是100,那么就是需要100%以上的下属完成准备,也就是当3、4完成2才能开始 ;当2、5、6完成1才能去打架
(3、4、5、6同时开始准备,3、4都完成过去了2天, 也就是第三天2可以开始准备(此时5也完成了),然后过了4天2、5、6都完成,1就可以去打架了,所以x==100时总共用了4天)
如果x是50,那么就是需要50%以上的下属完成准备,也就是当3或4完成 2才能开始 ;当2、5、6中有2个人(ceil(3/2)=2)完成 1才能去打架
(3、4、5、6同时开始准备,第一天结束4完成,此时已经满足“2号的50%及以上的下属完成”,于是2开始准备,第2天结束,2准备完成,此时5也完成了,这样就满足了“1号的50%及以上的下属完成”,1就可以去打架了,所以x==50时总共用了2天)
题目的上限T==3也就是必须要在3天内完成准备 显然x==100的时候需要4天不满足,而x==50的时候需要2天,满足。
=================================================
呃 到这里 才讲完题目...
好了 那么怎么做呢?
我们先倒着思考,要是我们已知x(百分比),继而来判断能不能满足“准备天数<=上限天数T”的条件 是不是就简单了很多呢,只要傻傻的相加就好了呢o(^▽^)o
好 那么我们就来枚举每一个百分比能不能满足条件 然后找个最大的!
浮点误差是$10^{-4}$那么0到100就总共$10^6$个情况,然后每个情况都要判断,最坏要加$10^4$次(n上限$10^4$)
那么就是O($10^4 imes 10^6$),Time Limit:500ms
啊哦不够额 ( ̄▽ ̄)
那就二分呗~~上下限分别是0和100,结束的条件就是 fabs(l-r)<$10^{-4}$ 咯~~
然后就结束了...
然后一交WA *****
坑爹的居然要LL
时间上限T明明只有$10^6$,$t_i$明明只有100,$10^4$个100加起来也才$10^6$嘛!为什么要LL!
对啊!!写这么大一坨就是为了吐槽一个LL啊!

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 const double eps=1e-4; 5 6 vector<LL> son[10005], tmp, tot; 7 int a[10005]; 8 LL sum[10005]; 9 10 int main() 11 { 12 int n, t; 13 scanf("%d%d", &n, &t); 14 for(int i=2;i<=n;i++) 15 { 16 int x; 17 scanf("%d%d",&x,&a[i]); 18 son[x].push_back(i); 19 } 20 a[1]=0; 21 double l=0, r=100, ans; 22 while(fabs(l-r)>=eps) 23 { 24 double m=(l+r)/2.0; 25 memset(sum, -1, sizeof(sum)); 26 tmp.clear(); 27 tmp.push_back(1); 28 while(!tmp.empty()) 29 { 30 int p=tmp[tmp.size()-1]; 31 if(!son[p].size()) 32 sum[p]=a[p], tmp.pop_back(); 33 else 34 { 35 if(sum[son[p][0]]==-1) 36 { 37 for(int i=0;i<son[p].size();i++) 38 tmp.push_back(son[p][i]); 39 continue; 40 } 41 tot.clear(); 42 for(int i=0;i<son[p].size();i++) 43 tot.push_back(sum[son[p][i]]); 44 sort(tot.begin(), tot.end()); 45 int pp; 46 for(int i=0;i<son[p].size();i++) 47 if((i+1)*100.0/son[p].size()>=m) 48 { 49 pp=i; 50 break; 51 } 52 sum[p]=tot[pp]+(LL)a[p]; 53 tmp.pop_back(); 54 } 55 } 56 if(sum[1]<=t) 57 ans=m, l=m; 58 else 59 r=m; 60 } 61 printf("%.7lf ", ans); 62 return 0; 63 }
