最小生成树
Kruskal
我们考虑这样一件事情,那就是,求出一个联通图,使得所有边权之和最小。
我们考虑这样一件事情,将所有边按照权值从小到大排序,每次取最小的,并且边的两端不连通的边连接。
于是说,这棵生成树两点之间的路径中,边权最大值最小,且边权之和最小。
证明详见 oi-wiki
复杂度:
- 暴力:(O(n^2+m))
- 二叉堆:(O((n+m)log n))
- ( ext{Fib}) 堆:(O(nlog n+m))
Prim
咕咕咕
Boruvka
咕咕咕
非严格次小生成树
枚举每一条边,倍增求生成树中, (u) 到 (v) 的路径中非严格小于这条边的最大权值,计算如果替换后的生成树大小。
对于每条边的答案取 (min) 。
严格最小生成树
同样倍增,求路径中严格小于新增边权的最大边,其余同上。
DAG 上的最小生成树
题意:给定一张 DAG ,用多条以 (1) 开始的路径覆盖尽可能多的点,并且使路径长度之和最短。
先用一遍 ( ext{dfs}) 求出可以到达的点的个数以及可能经过的所有边。
考虑给 DAG 上的每个点赋值点权,使得每条边上边的起点不小于边的终点。
将本来的 “以边权从小到大排序” 给为 “先以终点的点权从大到小排序,再以边权排序” 。
这样可以保证生成树上每一条边都是合法的。
$ exttt{code}$
#include<bits/stdc++.h>
using namespace std;
#define Maxn 100005
#define Maxm 1000005
typedef long long ll;
inline int rd()
{
int x=0;
char ch,t=0;
while(!isdigit(ch = getchar())) t|=ch=='-';
while(isdigit(ch)) x=x*10+(ch^48),ch=getchar();
return x=t?-x:x;
}
int n,m,tot,cnt,sum;
int h[Maxn],fa[Maxn];
int hea[Maxn],nex[Maxm<<1],ver[Maxm<<1];
ll edg[Maxm<<1],ans;
bool vis[Maxn];
void add(int x,int y,ll d){ ver[++tot]=y,nex[tot]=hea[x],hea[x]=tot,edg[tot]=d; }
struct Data { int u,v; ll w; }edge[Maxm<<1];
int Find(int x){ return (fa[x]==x)?x:(fa[x]=Find(fa[x])); }
bool cmp(Data x,Data y) // 按照点权、边权排序
{
if(h[x.v]!=h[y.v]) return h[x.v]>h[y.v];
return x.w<y.w;
}
void bfs() // 可以到达的点与边
{
queue<int> q;
q.push(1),vis[1]=true;
while(!q.empty())
{
int cur=q.front(); q.pop();
for(int i=hea[cur];i;i=nex[i])
{
edge[++cnt]=(Data){cur,ver[i],edg[i]};
if(!vis[ver[i]]) vis[ver[i]]=true,q.push(ver[i]);
}
}
}
int main()
{
n=rd(),m=rd();
for(int i=1;i<=n;i++) h[i]=rd(),fa[i]=i;
for(int i=1,x,y,d;i<=m;i++)
{
x=rd(),y=rd(),d=rd();
if(h[x]>=h[y]) add(x,y,1ll*d);
if(h[y]>=h[x]) add(y,x,1ll*d);
}
bfs();
sort(edge+1,edge+cnt+1,cmp);
for(int i=1,x,y;i<=cnt;i++)
{
x=Find(edge[i].u),y=Find(edge[i].v);
if(x!=y) fa[x]=y,sum++,ans+=edge[i].w;
}
printf("%d %lld
",++sum,ans);
return 0;
}
瓶颈生成树
咕咕咕
最小瓶颈路
咕咕咕
Kruskal 重构树
可悲的 Kruskal 只能满足两点之间路径最大边权最小,
贪婪的人们从不满足于弱小的 Kruskal,可悲的天才们沉迷于更为强大的结构,并残忍侵占了弱小的空间复杂度,将恶毒的眼光投向了可悲的时间复杂度。
于是我们考虑这样一件事情,那就是,用 Kruskal 够构建出一棵更为厉害的树,考虑将它叫做 Kruskal 重构树。
重构树将边权转移到点上,并每次连接两个连通块时都将两个连通块的顶部连到新建的点上。
比如我们现在有这样一棵树:
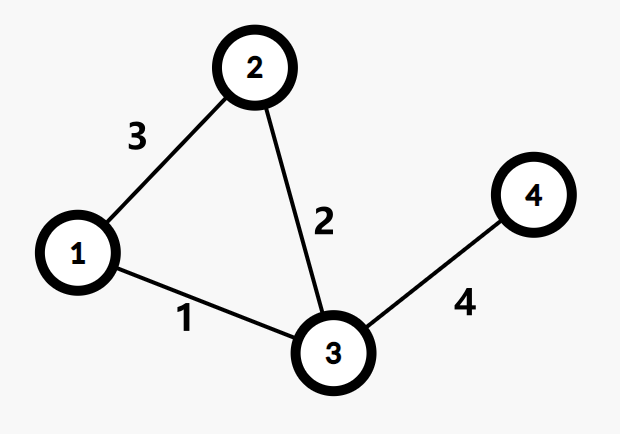
就可以生成这样一棵树:
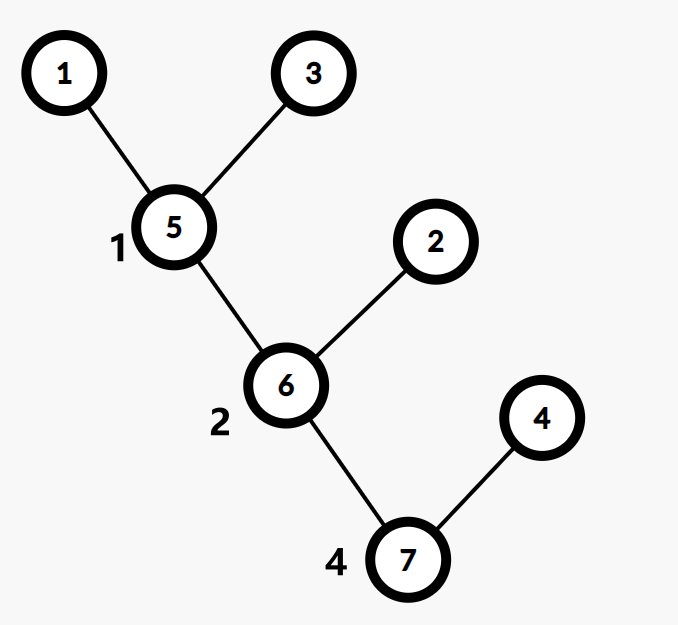
Kruskal 有一些优秀的性质:
-
它是一棵二叉树,满足堆的性质。
-
两个点的 (lca) 为这两个点的路径上的边权最小 (/) 大值。
-
一个根节点以下的所有点都可以用边权不超过 (/) 少于根节点权值的边联通,也就是说,到点 (x) 的简单路径上最小边权最大值 (le val) 的所有点 (y) 均在 Kruskal 重构树上的某一棵子树内,且恰好为该子树的所有叶子节点。
那么,根据这个性质,我们就可以快速解决 P4768 [NOI2018] 归程 啦!