排序是数据处理中十分常见且核心的操作,虽说实际项目开发中很小几率会需要我们手动实现,毕竟每种语言的类库中都有n多种关于排序算法的实现。但是了解这些精妙的思想对我们还是大有裨益的。本文简单温习下最基础的三类算法:选择,冒泡,插入。
先定义个交换数组元素的函数,供排序时调用
/**
* 交换数组元素
* @param arr
* @param a
* @param b
*/
public static void swap(int []arr,int a,int b){
arr[a] = arr[a]+arr[b];
arr[b] = arr[a]-arr[b];
arr[a] = arr[a]-arr[b];
}
简单选择排序
简单选择排序是最简单直观的一种算法,基本思想为每一趟从待排序的数据元素中选择最小(或最大)的一个元素作为首元素,直到所有元素排完为止,简单选择排序是不稳定排序。
在算法实现时,每一趟确定最小元素的时候会通过不断地比较交换来使得首位置为当前最小,交换是个比较耗时的操作。其实我们很容易发现,在还未完全确定当前最小元素之前,这些交换都是无意义的。我们可以通过设置一个变量min,每一次比较仅存储较小元素的数组下标,当轮循环结束之后,那这个变量存储的就是当前最小元素的下标,此时再执行交换操作即可。代码实现很简单,一起来看下。
代码实现
/**
* 简单选择排序
*
* @param arr
*/
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int min = i;//每一趟循环比较时,min用于存放较小元素的数组下标,这样当前批次比较完毕最终存放的就是此趟内最小的元素的下标,避免每次遇到较小元素都要进行交换。
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[min]) {
min = j;
}
}
//进行交换,如果min发生变化,则进行交换
if (min != i) {
swap(arr,min,i);
}
}
}
简单选择排序通过上面优化之后,无论数组原始排列如何,比较次数是不变的;对于交换操作,在最好情况下也就是数组完全有序的时候,无需任何交换移动,在最差情况下,也就是数组倒序的时候,交换次数为n-1次。综合下来,时间复杂度为O(n2)
冒泡排序
冒泡排序的基本思想是,对相邻的元素进行两两比较,顺序相反则进行交换,这样,每一趟会将最小或最大的元素“浮”到顶端,最终达到完全有序

代码实现
在冒泡排序的过程中,如果某一趟执行完毕,没有做任何一次交换操作,比如数组[5,4,1,2,3],执行了两次冒泡,也就是两次外循环之后,分别将5和4调整到最终位置[1,2,3,4,5]。此时,再执行第三次循环后,一次交换都没有做,这就说明剩下的序列已经是有序的,排序操作也就可以完成了,来看下代码
/**
* 冒泡排序
*
* @param arr
*/
public static void bubbleSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
boolean flag = true;//设定一个标记,若为true,则表示此次循环没有进行交换,也就是待排序列已经有序,排序已然完成。
for (int j = 0; j < arr.length - 1 - i; j++) {
if (arr[j] > arr[j + 1]) {
swap(arr,j,j+1);
flag = false;
}
}
if (flag) {
break;
}
}
}
根据上面这种冒泡实现,若原数组本身就是有序的(这是最好情况),仅需n-1次比较就可完成;若是倒序,比较次数为 n-1+n-2+...+1=n(n-1)/2,交换次数和比较次数等值。所以,其时间复杂度依然为O(n2)。综合来看,冒泡排序性能还还是稍差于上面那种选择排序的。
直接插入排序
直接插入排序基本思想是每一步将一个待排序的记录,插入到前面已经排好序的有序序列中去,直到插完所有元素为止。
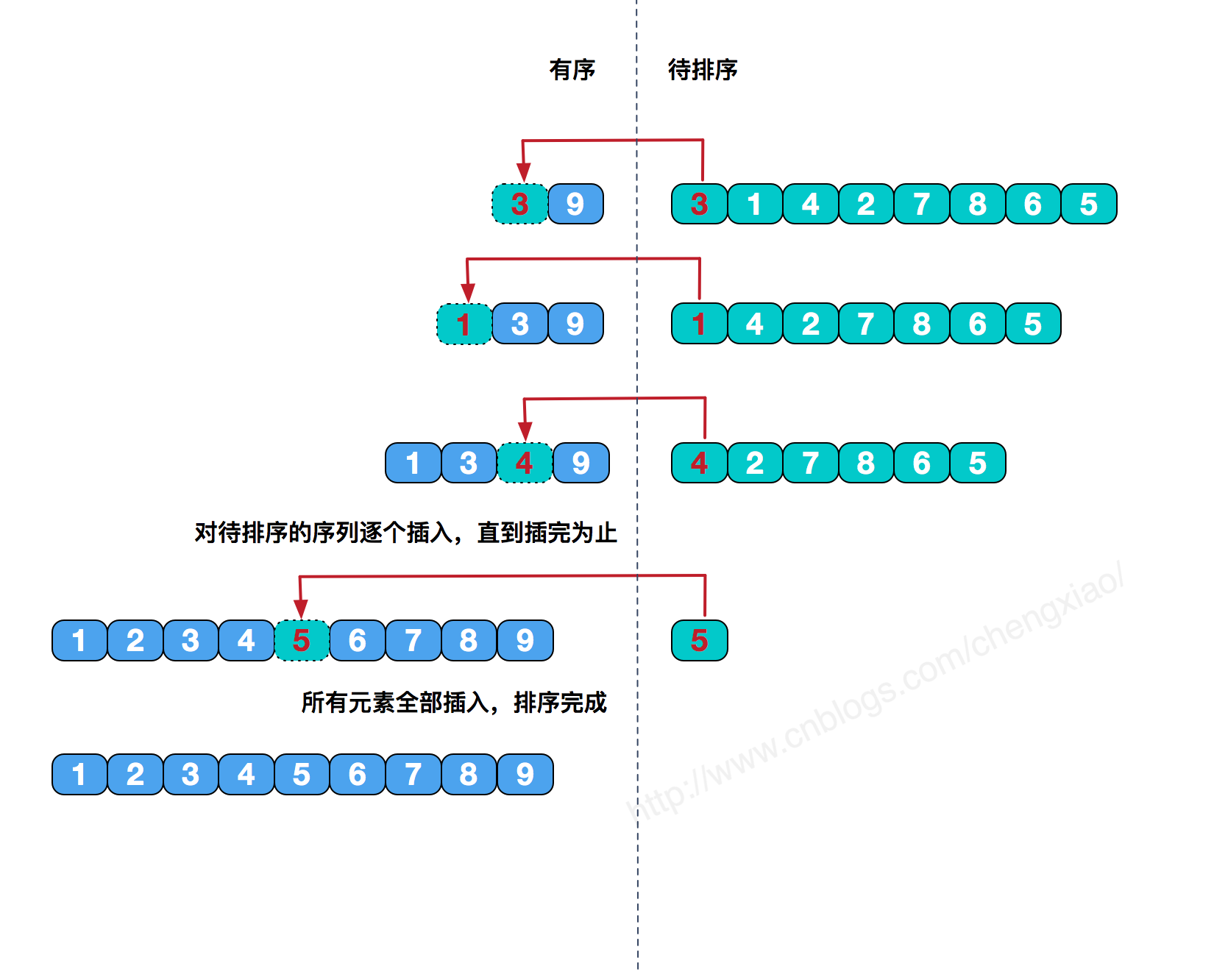
代码实现
/**
* 插入排序
*
* @param arr
*/
public static void insertionSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int j = i;
while (j > 0 && arr[j] < arr[j - 1]) {
swap(arr,j,j-1);
j--;
}
}
}
简单插入排序在最好情况下,需要比较n-1次,无需交换元素,时间复杂度为O(n);在最坏情况下,时间复杂度依然为O(n2)。但是在数组元素随机排列的情况下,插入排序还是要优于上面两种排序的。
总结
本文列举了排序算法中最基本的三种算法(简单选择,冒泡,插入),这三种排序算法的时间复杂度均为O(n2),后续会陆续更新其他更高阶一些的排序算法,时间复杂度也会逐步突破O(n2),谢谢支持。
希尔排序是希尔(Donald Shell)于1959年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序,同时该算法是冲破O(n2)的第一批算法之一。本文会以图解的方式详细介绍希尔排序的基本思想及其代码实现。
基本思想
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
简单插入排序很循规蹈矩,不管数组分布是怎么样的,依然一步一步的对元素进行比较,移动,插入,比如[5,4,3,2,1,0]这种倒序序列,数组末端的0要回到首位置很是费劲,比较和移动元素均需n-1次。而希尔排序在数组中采用跳跃式分组的策略,通过某个增量将数组元素划分为若干组,然后分组进行插入排序,随后逐步缩小增量,继续按组进行插入排序操作,直至增量为1。希尔排序通过这种策略使得整个数组在初始阶段达到从宏观上看基本有序,小的基本在前,大的基本在后。然后缩小增量,到增量为1时,其实多数情况下只需微调即可,不会涉及过多的数据移动。
我们来看下希尔排序的基本步骤,在此我们选择增量gap=length/2,缩小增量继续以gap = gap/2的方式,这种增量选择我们可以用一个序列来表示,{n/2,(n/2)/2...1},称为增量序列。希尔排序的增量序列的选择与证明是个数学难题,我们选择的这个增量序列是比较常用的,也是希尔建议的增量,称为希尔增量,但其实这个增量序列不是最优的。此处我们做示例使用希尔增量。
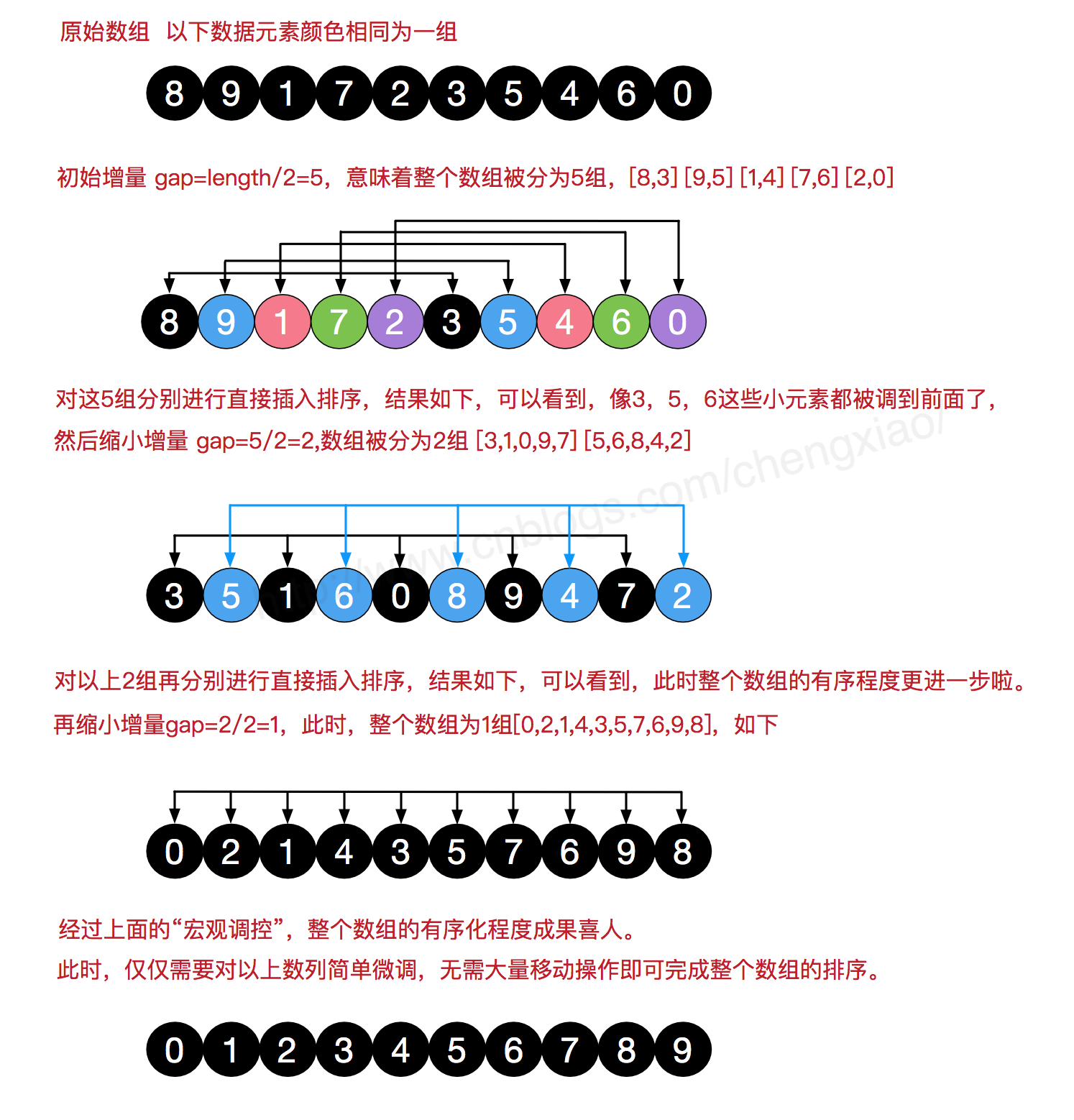
代码实现
在希尔排序的理解时,我们倾向于对于每一个分组,逐组进行处理,但在代码实现中,我们可以不用这么按部就班地处理完一组再调转回来处理下一组(这样还得加个for循环去处理分组)比如[5,4,3,2,1,0] ,首次增量设gap=length/2=3,则为3组[5,2] [4,1] [3,0],实现时不用循环按组处理,我们可以从第gap个元素开始,逐个跨组处理。同时,在插入数据时,可以采用元素交换法寻找最终位置,也可以采用数组元素移动法寻觅。希尔排序的代码比较简单,如下:
1 package sortdemo;
2
3 import java.util.Arrays;
4
5 /**
6 * Created by chengxiao on 2016/11/24.
7 */
8 public class ShellSort {
9 public static void main(String []args){
10 int []arr ={1,4,2,7,9,8,3,6};
11 sort(arr);
12 System.out.println(Arrays.toString(arr));
13 int []arr1 ={1,4,2,7,9,8,3,6};
14 sort1(arr1);
15 System.out.println(Arrays.toString(arr1));
16 }
17
18 /**
19 * 希尔排序 针对有序序列在插入时采用交换法
20 * @param arr
21 */
22 public static void sort(int []arr){
23 //增量gap,并逐步缩小增量
24 for(int gap=arr.length/2;gap>0;gap/=2){
25 //从第gap个元素,逐个对其所在组进行直接插入排序操作
26 for(int i=gap;i<arr.length;i++){
27 int j = i;
28 while(j-gap>=0 && arr[j]<arr[j-gap]){
29 //插入排序采用交换法
30 swap(arr,j,j-gap);
31 j-=gap;
32 }
33 }
34 }
35 }
36
37 /**
38 * 希尔排序 针对有序序列在插入时采用移动法。
39 * @param arr
40 */
41 public static void sort1(int []arr){
42 //增量gap,并逐步缩小增量
43 for(int gap=arr.length/2;gap>0;gap/=2){
44 //从第gap个元素,逐个对其所在组进行直接插入排序操作
45 for(int i=gap;i<arr.length;i++){
46 int j = i;
47 int temp = arr[j];
48 if(arr[j]<arr[j-gap]){
49 while(j-gap>=0 && temp<arr[j-gap]){
50 //移动法
51 arr[j] = arr[j-gap];
52 j-=gap;
53 }
54 arr[j] = temp;
55 }
56 }
57 }
58 }
59 /**
60 * 交换数组元素
61 * @param arr
62 * @param a
63 * @param b
64 */
65 public static void swap(int []arr,int a,int b){
66 arr[a] = arr[a]+arr[b];
67 arr[b] = arr[a]-arr[b];
68 arr[a] = arr[a]-arr[b];
69 }
70 }
总结
本文介绍了希尔排序的基本思想及其代码实现,希尔排序中对于增量序列的选择十分重要,直接影响到希尔排序的性能。我们上面选择的增量序列{n/2,(n/2)/2...1}(希尔增量),其最坏时间复杂度依然为O(n2),一些经过优化的增量序列如Hibbard经过复杂证明可使得最坏时间复杂度为O(n3/2)。希尔排序的介绍到此为止,关于其他排序算法的介绍也会陆续更新,谢谢支持。
