Task 1
小 W 和小 M 一起玩拼图游戏啦~ 小 M 给小 M 一张 N 个点的图,有 M 条可选无向边,每条边有一个甜蜜值,小 W 要选 K条边,使得任意两点间最多有一条路径,并且选择的 K条边甜蜜值之和最大。
对于 100%的数据:N,M<=100000
最小生成树裸题
时间复杂度 O(nlogn)
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<algorithm> 4 #include<iostream> 5 #include<string> 6 #include<string.h> 7 #include<math.h> 8 #define il inline 9 #define re register 10 using namespace std; 11 const int N=1000001; 12 struct edge{int x,y,z; 13 } e[N]; 14 int n,m,k,f[N],ans=0,cnt=0; 15 il bool cmp(edge a,edge b){ 16 return a.z>b.z; 17 } 18 il int getfather(int u){ 19 if(!f[u]) return u; 20 return f[u]=getfather(f[u]); 21 } 22 int main(){ 23 freopen("carpet.in","r",stdin); 24 freopen("carpet.out","w",stdout); 25 scanf("%d%d%d",&n,&m,&k); 26 for(int i=1;i<=m;i++) 27 scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].z); 28 sort(e+1,e+m+1,cmp); 29 for(int i=1,fx,fy;i<=m;i++){ 30 fx=getfather(e[i].x); 31 fy=getfather(e[i].y); 32 if(fx==fy) continue; 33 f[fx]=fy; 34 ans+=e[i].z; 35 cnt++; 36 if(cnt==k) break; 37 } 38 cout<<ans; 39 return 0; 40 }
Task 2
小 W 顺利地完成了拼图,该他给小 M 出题啦。 小 W 定义“!”运算符:
1、 N!k = N!(k-1) * (N-1)!k (N> 0 aNd k > 0)
2、 N!k = 1 (N = 0)
3、 N!k = N (k = 0)
现在小 W 告诉小 M N 和 k,小 M 需要说出 N!k 的不同约数个数。 为了降低难度,答案对 1000000009 取模就好了。
对于 100%的数据:N<=1000,k<=100
对于每个质数求对答案的贡献
时间复杂度 O(n^2*m/ln(n))
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<algorithm> 4 #include<iostream> 5 #include<string> 6 #include<string.h> 7 #include<math.h> 8 #define il inline 9 #define re register 10 using namespace std; 11 int prime[10001],tot=0; 12 bool chk[10001]; 13 int n,m,f[1010][110]; 14 long long ans=1; 15 int main(){ 16 freopen("calc.in","r",stdin); 17 freopen("calc.out","w",stdout); 18 memset(chk,false,sizeof(chk)); 19 scanf("%d%d",&n,&m); 20 for(int i=2;i<=n;i++){ 21 if(!chk[i]){ 22 prime[++tot]=i; 23 for(int j=i+i;j<=n;j+=i) 24 chk[j]=true; 25 } 26 } 27 for(int k=1;k<=tot;k++){ 28 memset(f,false,sizeof(f)); 29 for(int i=1,j;i<=n;i++){ 30 f[i][0]=0;j=i; 31 while(j%prime[k]==0){ 32 j/=prime[k];f[i][0]++; 33 } 34 } 35 for(int i=1;i<=m;i++) f[0][i]=0; 36 for(int i=1;i<=n;i++) 37 for(int j=1;j<=m;j++){ 38 f[i][j]=f[i-1][j]+f[i][j-1]; 39 if(f[i][j]>1000000009) f[i][j]-=1000000009; 40 } 41 ans=ans*(1ll+f[n][m])%1000000009ll; 42 } 43 // cout<<clock()<<endl; 44 cout<<ans; 45 return 0; 46 }
Task 3
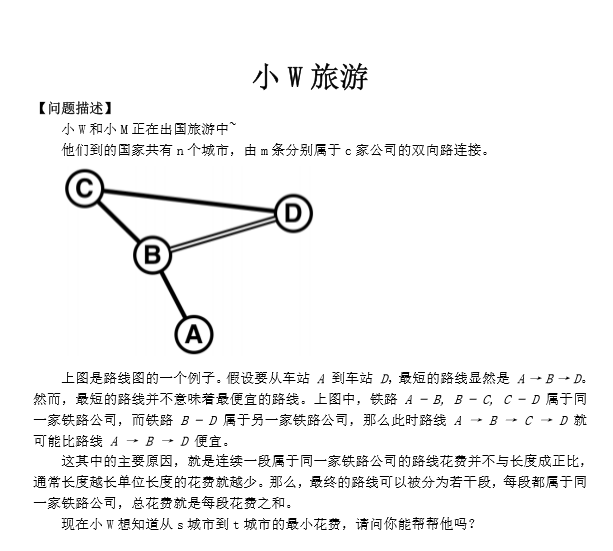

预处理只通过一个公司的线路,每个节点到其他节点的距离,暴力连边,跑最短路
时间复杂度O(cn^2logn)
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<algorithm> 4 #include<iostream> 5 #include<string> 6 #include<string.h> 7 #include<math.h> 8 #include<queue> 9 #define il inline 10 #define re register 11 using namespace std; 12 struct edge{int next,to,val; 13 } e[2000001]; 14 int n,m,c,s,t,M,p[100001],r[100001],q[100001],hs,h[100001]; 15 int d[100001],g[10001][101],v[100001],inq[100001]; 16 queue<int> que; 17 il void addedge(int x,int y,int z,int l){ 18 e[++M]=(edge){g[x][l],y,z};g[x][l]=M; 19 } 20 il void adde(int x,int y,int z){ 21 e[++M]=(edge){g[x][0],y,z};g[x][0]=M; 22 } 23 il void path(int h,int q){ 24 for(int i=1;i<=n;i++) d[i]=(1<<29); 25 d[h]=0;que.push(h); 26 while(!que.empty()){ 27 int h=que.front();que.pop();inq[h]=false; 28 for(int i=g[h][q];i;i=e[i].next){ 29 if(d[e[i].to]>d[h]+e[i].val){ 30 d[e[i].to]=d[h]+e[i].val; 31 if(!inq[e[i].to]){ 32 inq[e[i].to]=true; 33 que.push(e[i].to); 34 } 35 } 36 } 37 } 38 } 39 int main(){ 40 freopen("railway.in","r",stdin); 41 freopen("railway.out","w",stdout); 42 scanf("%d%d%d%d%d",&n,&m,&c,&s,&t); 43 for(int i=1,x,y,z,l;i<=m;i++){ 44 scanf("%d%d%d%d",&x,&y,&z,&l); 45 addedge(x,y,z,l); 46 addedge(y,x,z,l); 47 } 48 for(int i=1;i<=c;i++) 49 scanf("%d",&p[i]); 50 for(int i=1;i<=c;i++){ 51 for(int j=1;j<p[i];j++) 52 scanf("%d",&q[j]); 53 for(int j=1;j<=p[i];j++) 54 scanf("%d",&r[j]); 55 v[0]=0;q[0]=0; 56 for(int j=1;j<=p[i];j++) 57 v[j]=v[j-1]+(q[j]-q[j-1])*r[j]; 58 for(int j=1;j<=n;j++){ 59 path(j,i); 60 for(int k=1,l;k<=n;k++) if(k!=j&&d[k]<(1<<29)){ 61 l=lower_bound(q,q+p[i],d[k])-q-1; 62 adde(j,k,v[l]+(d[k]-q[l])*r[l+1]); 63 } 64 } 65 } 66 path(s,0); 67 if(d[t]<(1<<25)) cout<<d[t]<<endl; 68 else cout<<"-1"; 69 return 0; 70 }