【题解】 2019正睿普及五连测（三）T4——流浪地球

流浪地球

题目描述

太阳极速老化，为了生存下去，人类启动了史无前例的逃生计划。命名为“流浪地球”计划。
这个计划一开始，人类就付出了巨大的代价。当行星发动机启动的一刻，地球停止自转，板块移动引发了滔天海啸，为了让更多的人活下来，联合政府需要了解全球受灾情况，现在 (Cuber QQ) 受委托要完成中国区域的任务。
为了方便， (Cuber QQ) 把中国大陆板块分割成网格图，这个网格图有 (n) 行 (m) 列组成，每一个格子都有一个海拔高度。海啸引起了全球海平面上升，现在已知每一天，海平面都会上升 (1) 米（也就是说，第一天过后海平面是 (1) 米，第二天过后海平面是 (2) 米）。显然一开始，中国大陆板块是一个联通的整体，而 (Cuber QQ) 需要每天汇报给联合政府，当天过后中国大陆板块会被海水分割成几个板块。
注意，题目中所述的联通是指四个方向的联通。

输入格式

输入数据包含多组数据。第一行包含一个整数 (T) ，表示数据组数。
对于每一组数据，第一行包含两个整数 (n) 和 (m) ，表示网格大小。
第 (2) 至 (n+1) 行，每行 (m) 个用空格隔开的整数 (h_{i,j}) ，表示该网格的海拔。
第 (n+2) 行包含一个整数 (q) ，表示询问个数。接下来的一行，包含 (q) 个用空格隔开的整数 (x_i) ，表示询问在 (x_i) 天过后，板块的数量。

输出格式

对于每一组数据输出一行，包含(q)个用空格隔开的整数，表示对于每一个询问的答案。

样例

样例输入

1
4 5
1 2 3 3 1
1 3 2 2 1
2 1 3 4 3
1 2 2 2 2
5
1 2 3 4 5

样例输出

2 3 1 0 0

样例解释

下面的图中，白色的表示已经被海面淹没的区域，灰色是大陆区域。
第一天过后，有两个连通块：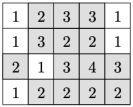
第二天过后，有三个连通块：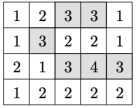

数据范围

• (1 leq T leq 5)
• (1 leq n, m leq 1000)
• (1 leq h_{i,j} leq 10^9)
• (1 leq q leq 10^5)

题目分析

这一道题很好想出暴力解法。对于每一个问题，我们只需要使用BFS搜索整个图，然后计算连通块数量。计算一下时间复杂度。遍历复杂度 (O(nm)) ，q次询问，T组数据，所以复杂度是 (O(T imes nmq)) ，此方法明显不可取。
我们可以发现，对于第 (i) 天的情况，我们只需要统计高度在 (i) 以上的连通块，而对于第 (i-a (a为正整数)) 天，我们发现第 (i) 天没有被淹没的方格也包括在内，所以我们只需要在第 (i) 天的基础上计算第 (i-a) 天的连通块数量就可以了。而连通块的维护可以用并查集。
如何统计连通块？这里介绍一种比较巧妙的解法：对于每一次连边（合并），如果这两个点是同一个集合（父节点相同），那么连通块的数量不变，否则，连通块数量-1。当然，记录连通块数量的变量 (sum) 要首先初始化为 (n) （点数）
那么我们就只剩下最后一个问题了，就是实现从第 (i) 天的答案递推到第 (i-a) 天，这里写出一种最简便的方法：
将所有的点和问题都压到一个结构体里面，使用一个成员变量tag记录这个结构体是一个点还是一次询问。如下：

struct Node
{
    bool tag; //false为点，true为询问
    int x,y,h; //x，y为坐标，h为高度，对于询问，使用x存储编号
}e[1100005];

然后，将e数组（包含点和询问）进行排序，以 (h) 为第一关键字，以 (tag) 为第二关键字。如下：

struct Node
{
    bool tag;
    int x,y,h;
    inline bool operator <(const Node &p)const
        { return (h==p.h)?(tag>p.tag):(h>p.h); } //重载小于运算符，不懂可以百度“C++运算符重载” 
}e[1100005];

这样子将 (e) 数组排序后，对于样例可以得到这样子的 (e) 数组：

e	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25
tag	1	1	0	1	0	0	0	0	0	1	0	0	0	0	0	0	0	0	1	0	0	0	0	0	0
x,y	5,0	4,0	3,4	3,0	3,3	3,5	2,2	1,3	1,4	2,0	1,2	4,5	4,4	4,3	4,2	3,1	2,4	2,3	1,0	4,1	1,5	2,1	1,1	3,2	2,5
h	5	4	4	3	3	3	3	3	3	2	2	2	2	2	2	2	2	2	1	1	1	1	1	1	1
经过观察，不难看出，我们只需要将整个 (e) 数组从 (1) 到 (n) 循环一遍，就可以很高效地计算答案了。时间复杂度 (O(nm+q)) 。

完整代码

#include <bits/stdc++.h> 
using namespace std;
int T,n,m,cnt,sum,q,fa[1100005],a[1100][1100],ans[100005];
int dirs[4][2]={{-1,0},{0,1},{1,0},{0,-1}};
struct Node //定义结构体
{
    bool tag;
    int x,y,h;
    inline bool operator <(const Node &p)const // 重载运算符，定义排序方式
        { return (h==p.h)?(tag>p.tag):(h>p.h); }
}e[1100005];
inline int find(int x) //并查集查询
    { return x==fa[x]?x:fa[x]=find(fa[x]); }
void link(int ux,int uy,int vx,int vy) //并查集合并
{
    int idu=(ux-1)*m+uy;
    int idv=(vx-1)*m+vy;
    int fu=find(idu),fv=find(idv);
    if(fu!=fv)
    {
        sum--; //如果两个点不在同一个连通块，连通块数量减一
        fa[fu]=fv;
    }
}
int main()
{
    scanf("%d",&T);
    while(T--)
    {
        memset(fa,0,sizeof(fa)); //初始化
        sum=cnt=0;
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++) for(int j=1;j<=m;j++)
        {
            scanf("%d",&a[i][j]);
            e[++cnt]={false,i,j,a[i][j]}; //存储点
            fa[cnt]=cnt;
        }
        scanf("%d",&q);
        for(int i=1;i<=q;i++)
        {
            int x;
            scanf("%d",&x);
            e[++cnt]={true,i,0,x}; //存储查询
        }
        sort(e+1,e+cnt+1); //排序
        for(int i=1;i<=cnt;i++) //遍历e数组
        {
            Node &p=e[i];
            if(p.tag)
                ans[p.x]=sum; //储存答案
            else
            {
                sum++;
                for(auto dir: dirs) //搜索与p相连的点
                {
                    int xx=p.x+dir[0],yy=p.y+dir[1];
                    if(xx<1 || yy<1 || xx>n || yy>m)    continue;
                    if(a[xx][yy]<p.h)    continue;
                    link(p.x,p.y,xx,yy); //连边
                }
            }
        }
        for(int i=1;i<=q;i++)    printf("%d ",ans[i]); //输出答案
        puts("");
    }
    while(1)    puts("while 大 法 好");
    return 0;
}