洛谷3195 玩具装箱（dp,斜率优化）

传送门：https://www.luogu.com.cn/problem/P3195

解题思路：

　　一道斜率优化入门题，代码量很少，比较符合dp题目的风格，但是式子写了满满两张纸，推了很久。

　　很明显是一道dp，可以轻易推出$dp[i]=min(dp[j]+(prefix[i]-prefix[j]+i-j-L-1)^{2})$，(i<j)，其中dp[i]表示前i个玩具的最小代价，prefix表示前缀和。

　　我们可以定义$a[i]=prefix[i]+i$，$b[i]=prefix[i]+i+L+1$，显然，a[i],b[i]都是定值

　　得到：$dp[i]=min(dp[j]+(a[i]-b[j])^{2})$

　　继续化简得：$dp[i]=dp[j]+a[i]^{2}-2*a[i]*b[j]+b[j]^{2}$

　　进行移项，得到$dp[j]+b[j]^{2}=2*a[i]*b[j]+dp[i]+a[i]^2$

　　这时，我们假设$x[i]=b[i]$，$y[i]=dp[j]+b[j]^{2}$

　　可以得到$y[j]=2*a[i]*x[j]+dp[i]+a[i]^{2}$

　　可以看出，(x,y)为i之前的若干个已求得的定点，要使得dp[i]最小，找一个点(x,y)，过(x,y)，斜率为2*a[i]的直线，与y周的截距最小。因此，问题就转化为了如何在[0,i-1]中找出这一个点。

　　

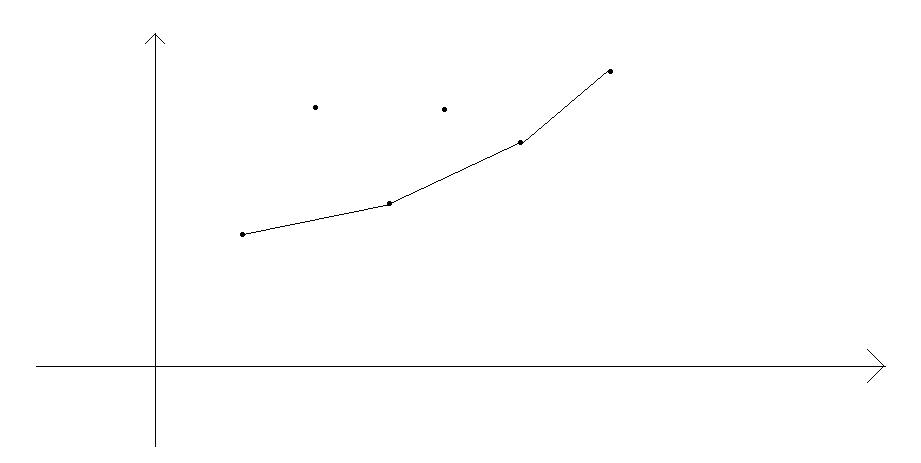
　　如图所示的点，不难发现最终，最终选择的点必然能形成一个下凸包。以图片中第二个点为例为例，设第1,3个点形成的斜率为k，若斜率大于k，第3个点必然优于第2个点，而斜率小于k时第1个点必然由于第2个点。因此，只需动态维护一个栈，计算前i个点形成的凸包，在从凸包中寻找答案，使用差积维护一个栈即可。但是若是所有点都在凸包上，暴力枚举点还是会达到$O(n^{2})$，在进行自习观察，可以发现斜率a[i]不光是定值，还是一个单调上升序列，因此斜率是递增的，所以，我们可以维护一个单调栈，若栈首两个点形成的斜率大于2*a[i]，就将首元素弹出，最后的栈首的元素就是最优的j，计算dp[i]即可。时间复杂度O(n)。

　　最后贴上代码：

#include<bits/stdc++.h>

using namespace std;
typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
typedef pair <ll,ll> pii;
#define rep(i,x,y) for(int i=x;i<y;i++)
#define rept(i,x,y) for(int i=x;i<=y;i++)
#define per(i,x,y) for(int i=x;i>=y;i--)
#define all(x) x.begin(),x.end()
#define pb push_back
#define fi first
#define se second
#define mes(a,b) memset(a,b,sizeof a)
#define mp make_pair
#define dd(x) cout<<#x<<"="<<x<<" "
#define de(x) cout<<#x<<"="<<x<<"
"
#define debug() cout<<"I love Miyamizu Mitsuha forever.
"
const int inf=0x3f3f3f3f;
const int maxn=5e4+5;
ll dp[maxn];
ll prefix[maxn];
int n;ll l;
ll a(int pos)
{
    return pos+prefix[pos];
}
ll b(int pos)
{
    return pos+prefix[pos]+l+1;
}
ll x(int pos)
{
    return b(pos);
}
ll y(int pos)
{
    return dp[pos]+b(pos)*b(pos);
}
int q[maxn];

ll chaji(ll x1,ll y1,ll x2,ll y2)
{
    return x1*y2-x2*y1;
}

double xielv(int a,int b)
{
    return ( double( y(b)-y(a) ) ) / (x(b)-x(a));
}        
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    cin>>n>>l;
    prefix[0]=0;
    rept(i,1,n)
    {
        cin>>prefix[i];
        prefix[i]+=prefix[i-1];
    }
    int head=0,tail=0;
    dp[0]=0;
    q[0]=0;
    rept(i,1,n)
    {
        while(head<tail&&chaji( x(q[head])-x(q[head+1]),y(q[head])-y(q[head+1]),1,2*a(i) )<0 ) head++;
        dp[i]=y(q[head])+a(i)*a(i)-2*a(i)*x(q[head]);
        while(head<tail&&chaji( x(i)-x(q[tail-1]),y(i)-y(q[tail-1]),x(q[tail-1])-x(q[tail]),y(q[tail-1])-y(q[tail]) )<0 ) tail--;
        q[++tail]=i;
    }
    cout<<dp[n]<<"
";
    return 0;
}