算法思路:
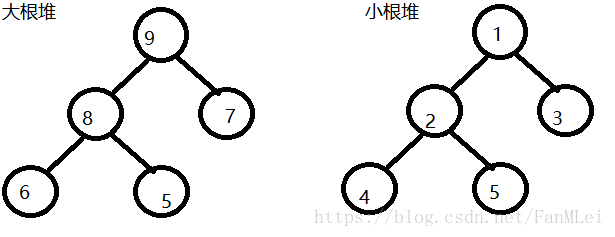
堆:分为大根堆和小根堆
大根堆:一棵完全二叉树,满足任意一节点都比其孩子节点大。
小根堆:一棵完全二叉树,满足任意一节点都比其孩子节点小。
堆排序流程:
- 构造堆
- 得到堆顶元素,为最大元素
- 去掉堆顶,将堆的最后一个元素放到堆顶,然后调整重新使堆有序
- 堆顶元素为第二大的元素
- 重复第三步直到堆变空
例如以[4, 5, 3, 6, 1, 2 ]为例:
准备知识:
在以顺序储存的完全二叉树中,父子节点的关系(下标):
- 父节点和左孩子:左孩子下标 = 父节点下标 * 2 + 1
- 父节点和右孩子:右孩子下标 = 父节点下标 * 2 + 2
- 子节点和父节点: 父节点下标 = (子节点下标 - 1) // 2
- 最后一个非叶子节点:n // 2 -1
代码实现:
def sift(nums, low, high):
"""
调整堆,使堆有序
:param nums: list
:param low: 根节点
:param high: 尾节点(树的最后一个)
:return:
"""
temp = nums[low]
i = low
j = 2 * i + 1
while j <= high: # 当前i位置为叶子节点, j超过high了
# 找更大的子节点
if j + 1 <= high and nums[j+1] > nums[j]: #
j = j + 1
if temp < nums[j]:
nums[i] = nums[j]
i = j
j = 2 * i + 1
else: # temp 大于两个子节点
break
nums[i] = temp
def heap_sort(nums):
# 建堆
l = len(nums)
for i in range(l//2-1, -1, -1):
# i是建堆时要调整的子树的根节点下标
sift(nums, i, l-1)
for i in range(l - 1, -1, -1):
# 当前的high值
nums[i], nums[0] = nums[0], nums[i]
sift(nums, 0, i-1)内置函数:
Python内置模块heapq帮我们实现了堆排序,内置函数用的是小根堆,上面的代码是大根堆,差别不大,heapq模块主要包括三个函数:
-
heapify(list) 建小根堆 把传入的list变成小根堆
-
heappush(heap_list, item)向已经建好的堆中增加数据
-
heappop(heap_list) 输出小根堆中最小值
import heapq
nums = [3, 2, 1, 0, 6]
heapq.heapify(nums)
print(nums)
# [0, 2, 1, 3, 6]
heapq.heappush(nums, 4)
print(nums)
# [0, 2, 1, 3, 6, 4]
print(heapq.heappop(nums))
# 0
print(heapq.heappop(nums))
# 1
print(heapq.heappop(nums))
# 2