最大连续子数组和求解问题

题目:最大连续子数组和求解问题

一.背景：

问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。

--引用自《百度百科》

---

二.解题

方法一：暴力解法

看到题目瞬间想到大一初次接触数组时，求解数组和最大问题。但当时我就是采用将全部和算出来再进行比较的方法。
所以这次我也将采用暴力解法，直接算出所有的子数组的和，然后在所有数组和中挑选最大的进行输出。

[代码地址] ( https://git.dev.tencent.com/dtid_85494e5bcaedfaa6/zuidazishuzuqiuhe.git )

流程图如下：

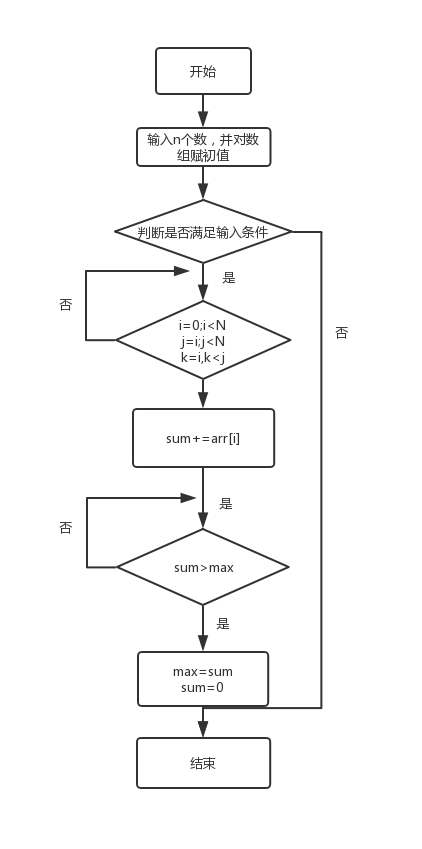
代码如下：

/*
问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。
当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
*/

/*
问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。
当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
*/

#include <stdio.h>
#include<stdlib.h>

int MMax(int arr[], int N)
{
	int i = 0, j = 0, k = 0, sum = 0,max=0;
	for (i = 0; i < N; i++)
	{
		for (j = i; j < N; j++)
		{
			for (k = i; k <= j; k++)
			{
				sum = sum + arr[k];
			}
			if (sum > max)
			{
				max = sum;
			}
			sum = 0;
		}
	}
	return max;
}
int main()
{
	int *arr;
	int N = 0, input=0, i=0;
	int Max = 0;
	scanf_s("%d", &N);
	arr = (int*)malloc(sizeof(int)*N);
	int minus = 0;
	if (N < 0)
	{
		printf("ERROR");
		return 0;
	}

	//对数组进行赋初值，并且记录负数个数
	for (i = 0; i < N; i++)
	{
		scanf_s("%d", &input);
		arr[i] = input;
		if (input < 0)
		{
			minus++;
		}
	}

	//如果全为负数，直接输出0，并结束程序
	if (minus == N)
	{
		printf("0");
		return 0;
	}

	//对最大子数组进行求解并输出
	Max = MMax(arr, N);
	printf("%d", Max);
	return 0;
	

}

下面进行代码测试环节：我选择判定/条件覆盖

测试样例	测试结果	说明
n=6，arr[6]={-2,11,-4,13,-5,-2}	20	正常情况最大子段和为20
n=5, arr[5] = { -1,2,3,-6,7 }	7	结果为最大的一个正数
n=6, arr[6]={-2,-11,-4,-13,-5,-2}	0	数组中都是负数，所以为0
n=6, arr[6]={1,2,3,4,5,6}	21	结果中都是正数，结果为正数全部相加

测试代码如下：

#include "stdafx.h"
#include "CppUnitTest.h"
#include "..Max标头.h"

using namespace Microsoft::VisualStudio::CppUnitTestFramework;

namespace UnitTest1
{		
	TEST_CLASS(UnitTest1)
	{
	public:
		
		TEST_METHOD(TestMethod1)
		{
			int arr[6] = { -2,11,-4,13,-5,-2 }, max;
			max = Max(arr, 6);
			Assert::AreEqual(max, 20);
		}
		TEST_METHOD(TestMethod2)
		{
			int arr[5] = { -1,2,3,-6,7 }, max;
			max = Max(arr, 5);
			Assert::AreEqual(max, 7);
		}
		
		TEST_METHOD(TestMethod3)
		{
			int arr[6] = { -2,-11,-4,-13,-5,-2 }, max;
			max = Max(arr, 6);
			Assert::AreEqual(max, 0);
		}

		TEST_METHOD(TestMethod4)
		{
			int  arr[6] = { 1,2,3,4,5,6 }, max;
			max = Max(arr, 6);
			Assert::AreEqual(max, 21);
		}

	};
}

测试结果如下：

---

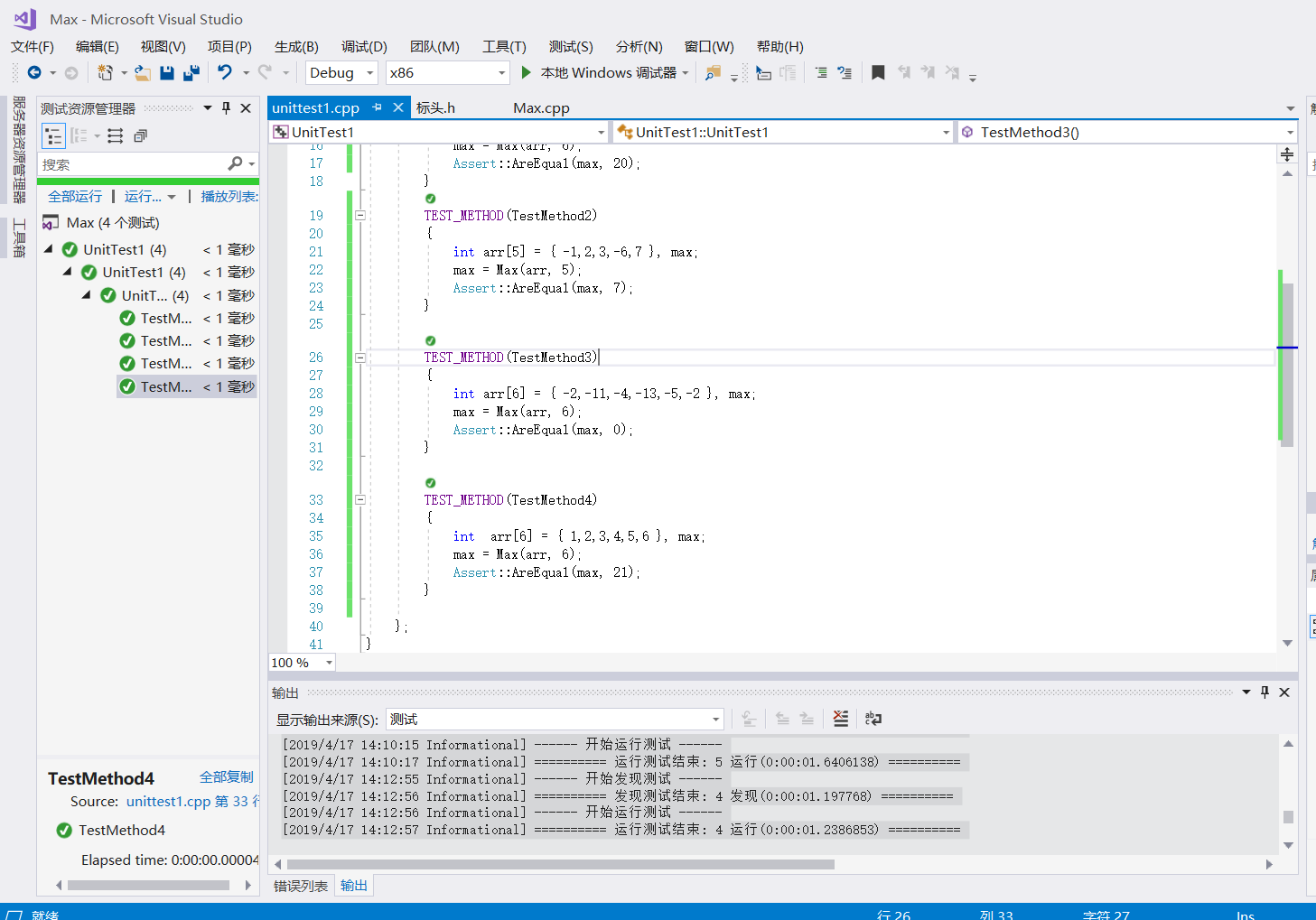
方法二：不太暴力的解法

身为计算机的学生，理应多多思考好的算法。且第一种方法在数据量较大时，所需时间较长。
所以我在同学的点拨下又找到一种方法。
代码如下：

#include <stdio.h>
#include <stdlib.h>

int main()
{
    int *arr;
	int N = 0, input=0, i=0;
	int sum = 0, max = 0;
	scanf_s("%d", &N);
	arr = (int*)malloc(sizeof(int)*N);
	int minus = 0;

	//对数组进行赋初值，并且记录负数个数
	for (i = 0; i < N; i++)
	{
		scanf_s("%d", &input);
		arr[i] = input;
		if (input < 0)
		{
			minus++;
		}
	}

	//如果全为负数，直接输出0，并结束程序
	if (minus == N)
	{
		printf("0");
		return 0;
	}

    //对最大子数组进行求解
    max=arr[1];
	for(i=0;i<N;i++)
    {
        sum=sum+arr[i];
        if (sum>max)
        {
            max=sum;
        }
        if (sum <0)
        {
            sum=0;
        }
    }
    printf("%d",max);

    return 0;

}

下面进行代码测试环节：我选择判定/条件覆盖

测试样例	测试结果	说明
n=6，arr[6]={-2,11,-4,13,-5,-2}	20	正常情况最大子段和为20
n=5, arr[5] = { -1,2,3,-6,7 }	7	结果为最大的一个正数
n=6, arr[6]={-2,-11,-4,-13,-5,-2}	0	数组中都是负数，所以为0
n=6, arr[6]={1,2,3,4,5,6}	21	结果中都是正数，结果为正数全部相加

测试代码如下：

#include "stdafx.h"
#include "CppUnitTest.h"
#include "..Max标头.h"

using namespace Microsoft::VisualStudio::CppUnitTestFramework;

namespace UnitTest1
{		
	TEST_CLASS(UnitTest1)
	{
	public:
		
		TEST_METHOD(TestMethod1)
		{
			int arr[6] = { -2,11,-4,13,-5,-2 }, max;
			max = Max(arr, 6);
			Assert::AreEqual(max, 20);
		}
		TEST_METHOD(TestMethod2)
		{
			int arr[5] = { -1,2,3,-6,7 }, max;
			max = Max(arr, 5);
			Assert::AreEqual(max, 7);
		}
		
		TEST_METHOD(TestMethod3)
		{
			int arr[6] = { -2,-11,-4,-13,-5,-2 }, max;
			max = Max(arr, 6);
			Assert::AreEqual(max, 0);
		}

		TEST_METHOD(TestMethod4)
		{
			int  arr[6] = { 1,2,3,4,5,6 }, max;
			max = Max(arr, 6);
			Assert::AreEqual(max, 21);
		}

	};
}

测试结果如下：

总结：

通过本次实验，我仔细研究明白了子数组最大和的求法。而且深入的了解判定/条件的测试方法并进行了大量练习。通过这次实验，我已经可以熟练进行代码测试，对测试的思想以及测试工具都有了更深一步的掌握。我会在日后学习中大量练习这种测试方法，为我日后的工作学习做好准备。