思路:
(quad)说实话,第一眼看这题想到的是线段树,但无奈 (1<=n<=10^ 9) ,离散化有点复杂,动态开点又不会,所以使用了一种离线做法,跑的还贼快(大雾
(quad)现将所有操作存起来, (dir) 表示方向, (1) 为上, (0) 为左,然后按 (x) 为第一关键字, (t) (时间)为第二关键字排序(我第一次 (WA) 就是这个原因)
struct node{
int x,y,t,dir;
}a[N],b[N];
il bool cmp(node a1,node a2){return a1.x==a2.x?a1.t<a2.t:a1.x<a2.x;}
for(re i=1,x,y;i<=m;i++)
{
x=read(),y=read();ch=getchar();
if(ch=='U')a[i]=(node){x,y,i,1};
else a[i]=(node){x,y,i,0};
}
sort(a+1,a+m+1,cmp);
(quad)然后考虑每一种情况,显然,向左的操作会被前面的向上的操作影响(前面的指 (x) 小于 (TA) ,且时间 (t) 也小于 (TA) 的),向上的操作会被后面的向左的操作影响(后面指 (x) 大于 (TA) ,但时间 (t) 小于 (TA) 的),所以可以发现相邻的向上的操作和向左的操作会互相影响(相邻是指x相邻),这时候我们就要判断它们的时间先后了。
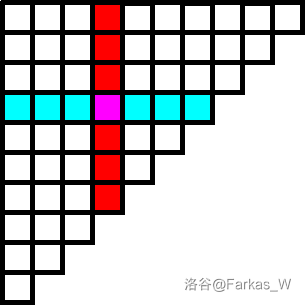
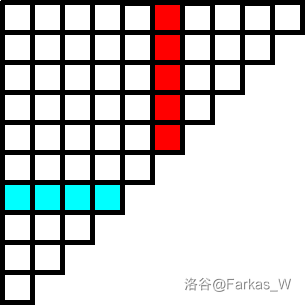
(quad)然后我们就可以发现只有向上的操作在前,才有可能对后面的向左的操作产生影响(先不考虑时间),另外向上的也只被后面的第一个向左的所影响,所以向上的暂时无法得出答案,先放进一个栈中存储,只有遇到向左的就把栈中的时间大于 (TA) 的更新答案,遇到一个时间小于 (TA) 的就被堵住了,这时候就更新它自己的答案。(这里的 (TA) 指的是向左的操作)
(quad)现在来模拟一个数据来理解一下。
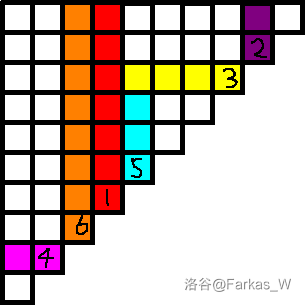
(quad)先排序,对于操作 (4) ,此时栈是空的,直接更新答案,对于操作 (6) 、操作 (1) 和操作 (5) ,直接存进栈里,等到操作 (3) 时开始退栈,先比较栈顶的时间,更新操作 (5) 的时间,将 (5) 退出,然后和操作 (1) 比较,停止退栈,更新操作 (3) 本身的答案,最后将操作 (2) 压进栈中,循环结束,将栈中元素全部退出,这些把一列的巧克力都吃光了。
(quad)如果还不理解就看看完整代码吧,附带注释。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
#define re register int
#define int long long
#define il inline
il int read()
{
int x=0,f=1;char ch=getchar();
while(!isdigit(ch)&&ch!='-')ch=getchar();
if(ch=='-')f=-1,ch=getchar();
while(isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
return x*f;
}
il void print(int x)
{
if(x<0)putchar('-'),x=-x;
if(x/10)print(x/10);
putchar(x%10+'0');
}
const int N=2e5+5;
int n,m,ans[N],tot;
struct node{
int x,y,t,dir;
}a[N],b[N];
il bool cmp(node a1,node a2){return a1.x==a2.x?a1.t<a2.t:a1.x<a2.x;}//注意
signed main()
{
n=read();m=read();char ch;
for(re i=1,x,y;i<=m;i++)
{
x=read(),y=read();ch=getchar();
if(ch=='U')a[i]=(node){x,y,i,1};//dir=1表示向上,Up
else a[i]=(node){x,y,i,0};//dir=0表示向左,Left
}
sort(a+1,a+m+1,cmp);//排序
b[0]=(node){0,n+1,0,1};//处理边界
for(re i=1;i<=m;i++)
{
if(a[i].x==a[i-1].x&&a[i].y==a[i-1].y)continue;//如果遇到相同的就跳过,后面的一个巧克力都吃不到
if(a[i].dir)b[++tot]=a[i];
else {
while(b[tot].t>a[i].t){//条件:时间更大
ans[b[tot].t]=b[tot].y-a[i].y;//更新答案
tot--;//退栈
}
ans[a[i].t]=a[i].x-b[tot].x;//不能再退栈时,更新自己的答案
}
}
while(tot){
ans[b[tot].t]=b[tot].y;//将还在栈里的退出来
tot--;
}
for(re i=1;i<=m;i++)print(ans[i]),putchar('
');
return 0;
}