
input
2 3
2 1 2
2 2 3
output
1
input
1 3
3 1 2 3
output
6
input
2 4
2 1 2
3 2 3 4
output
2
input
3 7
2 1 2
2 3 4
3 5 6 7
output
24
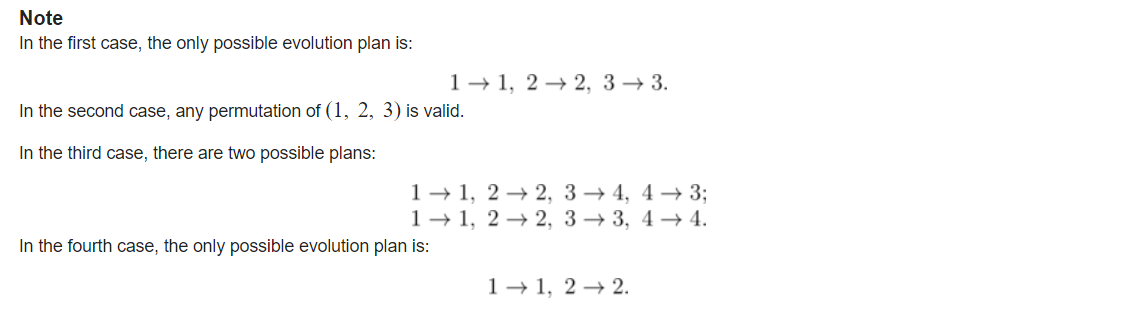
题意
一共有m种宝可梦,有n个道馆每个道馆有gi个宝可梦,设计一个转换方法,该方法满足 f(x) = y ---> 将x种宝可梦转化成y种
宝可梦转化后没个道馆中的每种宝可梦数量必须不变,问一个可以设计多少种转化方法
思路
如果一种转换方法f(x) = y成立,那么满足,x所在的道馆y也在,并且x与y在同一家道馆的数量必须相同,所以我一直接用vector
保存某一种宝可梦在几号道馆中存在,最后对vector进行一个排序,若相邻两个vector相同那么说明这两种宝可梦是可以满足转化
的,记录下当前有几对宝可梦t是满足可转化的,答案就是累乘t!
代码
#pragma GCC optimize(2)
#include<unordered_map>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<string>
#include<vector>
#include<queue>
#include<stack>
#include<cmath>
#include<map>
#include<set>
#define Buff ios::sync_with_stdio(false)
#define rush() int Case = 0; int T; cin >> T; while(T--)
#define rep(i, a, b) for(int i = a; i <= b; i ++)
#define per(i, a, b) for(int i = a; i >= b; i --)
#define reps(i, a, b) for(int i = a; b; i ++)
#define clc(a, b) memset(a, b, sizeof(a))
#define Buff ios::sync_with_stdio(false)
#define readl(a) scanf("%lld", &a)
#define readd(a) scanf("%lf", &a)
#define readc(a) scanf("%c", &a)
#define reads(a) scanf("%s", a)
#define read(a) scanf("%d", &a)
#define lowbit(n) (n&(-n))
#define pb push_back
#define sqr(x) x*x
#define rs x<<1|1
#define y second
#define ls x<<1
#define x first
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int, int>PII;
const int mod = 1e9+7;
const double eps = 1e-6;
const int N = 1e6+7;
int n, m;
vector<int> a[N];
int main()
{
Buff;
cin >> n >> m;
rep(i, 1, n)
{
int g;
cin >> g;
rep(j, 1, g)
{
int x;
cin >> x;
a[x].push_back(i);
}
}
sort(a+1, a+m+1);
int c = 1, res = 1;
rep(i, 2, m)
if(a[i] == a[i-1])
{
c ++;
res = 1ll * res * c % mod;
}
else c = 1;
cout << res << endl;
return 0;
}