APICS理论部分
先看一下APICS字典关于重排假设的定义:
rescheduling assumption--A fundamental assumption of MRP logic that existing open orders can be rescheduled in nearer time periods far more easily than new orders can be released and received.As a result,planned order receipts are not crteated until all scheduled receipts have been applied to cover gross requirements.
翻译一下大体意思是:
重排假设--MRP逻辑的基本假设,它认为重新排产短时期内的未结订单(指的是已经开工的或者订购的但还没有入库的生产订单或者采购订单)比从重新下达和接收新的计划订单容易得多。如果按照这个逻辑的话,在所有的预计接收量全部覆盖毛需求之前将不会产生新的计划订单。
Apics字典中的解释言简意赅,很多问题没有展开讲,关于这个问题<<MRPII Standard System>>这本书有很详细的论述。第6章<<The Netting and Exception Checking Logic of MRPII>>,下面大体说一下它讲述的意思,如果有理解不正确的地方,还望同行多多指教。
在创建和下达一个新的计划订单之前,净需求的逻辑假定已经存在的预计接收量将会被重排到一个更早的日期来满足需求。比如,下周存在一个未满足的需求,车间里有个生产订单还没完工,净需求的计算逻辑会假定这个订单会加速完成来满足需求。这种假设实际上是反映世界的真实情况,注意重排假设并不会假定这个生产订单一定会被加速并在下周完成,它只是假设如果有订单能在下周完工的话,应该是在车间加工的订单而不是新创建的订单,注意,净需求的计算逻辑并不会修改预计接收量的日期,它只是在做净需求计算时使用这个订单而已。在这本书的附录三里介绍了如果MRP不使用重排假设会产生的问题:
1.安排一个新的订单在已经存在的订单完工前完工,会让计划员或者采购员很难理解,一个已经在车间生产的订单显然会比一个新创建的订单更有可能先完成。向车间下达一个新的订单并要求它在已存在的订单前完工,没有意义。极端情况下,逻辑会变成不是根据要制造的产成品的数量,而是根据排产更改的次数去订购材料。
2.不考虑重排假设的会引起产品计划的不正确,并且只是问题的一部分,一旦一个新的订单被安排了,该产品的零部件的毛需求就会产生,由于这个新的订单的安排就是不正确的,那么它所产生的零部件的毛需求也不会正确,这样毛需求,计划订单和异常信息都会很快变得毫无意义,系统也就失败了,因为它已经不能用来模拟现实了。
上面的这些理论主要是介绍MRPII为什么要使用重排假设,那么系统应该怎么提醒计划员那?<<MRPII Standard System>>也给出了解决方法,向计划员提供重排异常信息。
当一个预计接收量的预计入库日期不足够早时,就会产生物料短缺,在这种情况下,就应该产生一个异常信息提示这个订单的完工日期应该提前以防止物料短缺的发生。
如果一个预计接受量的预计完工日期过早时,同样严重的问题也会产生,要么有用的能力用来生产错误的产品,或者正常的优先级逻辑将不能辨别什么是真正需要的和什么时候需要。所以在这种情况下,也应该产生一个异常信息,来提示需要将这个订单的完工入库日期向后排。
另外,有个争论就是为什么不让系统自己更改预计接收量的完工入库日期?这本书的作者的观点是,这是人的职责,计算机只负责提供异常信息,至于要不要调整是计划员的工作,计划员要为这件事情负责而不是计算机,即便是计算机帮计划员自动更改了日期,计划员还是有责任去重新看一遍看是否正确,与其这样还不如,让计划员自己去改。
AX中的实现
在进行之前,根据前面的描述,我们需要明确一个概念,在APICS字典中提到能修改的是in nearer time periods ,意思是更改相对近的期间内的预计收货量的的入库日期,但是在计算机实现的时候不能用nearer这样的人性化的模糊概念,必须要能量化,AX提供了两个参数来量化这个时间,也就是正天数和负天数,Positive Days和Negative Days.
主计划->设置->覆盖范围->覆盖范围组->常规选项卡
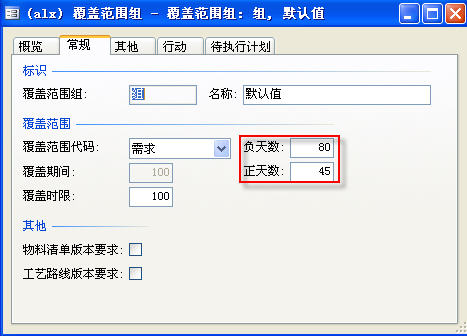
对照APICS理论部分的内容就很容易理解这个负天数和正天数的含义了,按照重排假设,如果预计收货量的入库日期比需求日期晚,那么系统需要给出一个将预计收货量的入库日期提前的提示信息,但是不能用无限期天数,比如让计划员修改几年后的一个生产订单的入库日期,那个开工日期还早着那,大可不必考虑。
负天数就是用来定义系统会考虑交货日期后多少天入库的预计收货量的入库日期。比如现在有一个需求日期为2009-09-18的销售订单,系统里已经有了2009-09-25和2009-10-28的两张还未入库的生产订单,如果负天数设置为10天,那么系统就只会考虑2009-09-25这张生产订单,给出提示修改它的完工入库日期和数量,而不会考虑2009-10-28的这张生产订单了,因为这张订单在需求日期的10天后。
同样正天数就比较好考虑了,正如上文提到的那样,<<MRPII Standard System>>也说了 如果一个预计接受量的预计完工日期过早时,也应该产生一个异常信息,来提示需要将这个订单的完工入库日期向后排。那么多久之前的预计收货量需要提示其延后那?就是这个正天数的作用了,这个天数不能设置的太小,要不然需求日期-正天数就会大于当前日期,那么就连当前的现有量都不会考虑了,这就不对了,一般设置不能小于该物料的提前期,因为一般情况下计划员至少要在提前期内开工要不然就不能按时完工了,所以完工日期-提前期应该是不大于当前日期的。
明白了正天数和负天数的概念,就比较容易看在AX里是怎么实现重排假设的了。
为了方便说明问题,简便期间,我们只创建一个简单的物料RA,其物料类型为物料。然后创建一个销售订单,让其产生毛需求,交货日期为2009-09-30,如下图所示:
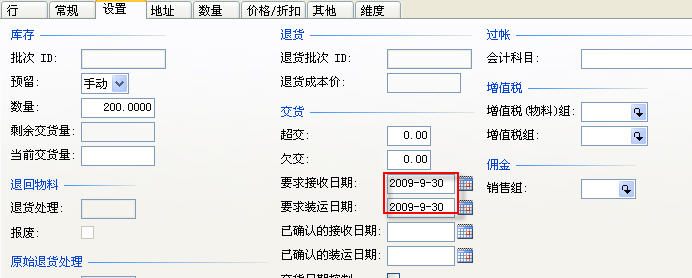
这样物料RA就会有需求日期为2009-09-30的毛需求了,这时运行主计划,可以看到RA的计划采购订单。

这没有问题。
现在测试它的重排逻辑,先测试如果系统存在一个交货日期在2009-09-30之前预计接收量,假设收货日期为2009-09-20,我们让它在有效的范围内,那么正天数至少不能小于10天,我们设置正天数为20天,创建一个采购订单,设定交货日期为2009-09-20,数量恰好满足需求为200,如下图所示:
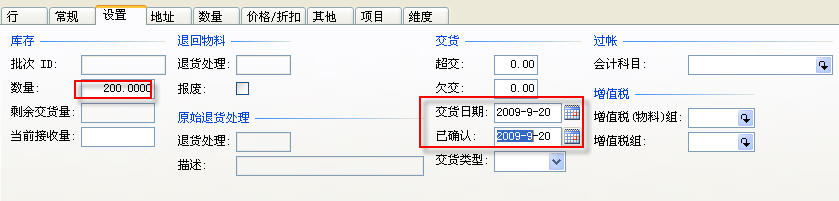
这时再运行Master Planning,理论上应该是不产生计划采购订单了,并且应该产生一条提示信息,让采购订单延后10天到2009-09-30交货。我们可以验证一下,运行Master Planning,查看计划订单不会看到有RA的计划采购订单生成了,再去看一下是否有让我们延迟交货的消息产生。
主计划->报表->覆盖范围->行动
选择我们刚刚运行的主计划,物料选择RA,如下图所示:
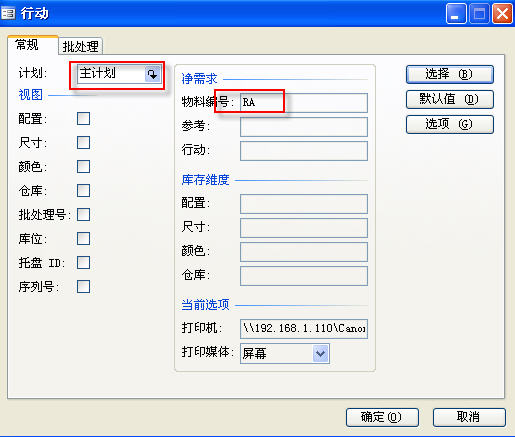
点击确定,查看结果

显然这个结果是符合预期的。
我们再来测试两种情况,如果已经存在的采购订单的数量大于需求,比如采购订单的数量是300,它应该怎么处理那?理论上,延期这个应该跟上面一样的,但是数量应该减少100个,修改采购订单数量为300,同样的步骤运行主计划,查看行动消息如下:

显然这个结果也是正确的。
最后一种情况,如果采购订单上的数量不足200个,比如是100个,应该怎么处理那?理论上应该,延期并且增加数量才对。修改采购订单数量为100,运行主计划,查看计划订单,我们会发现产生了一个数量为100的计划采购订单,如下图所示:

这条记录对应的消息如下:

AX给出的建议是取消这张计划订单,那么它对采购订单的建议采取什么动作那?运行报表查看结果如下:

无疑这个结果也是合情合理的,给了计划员两种选择,要么增加原来采购订单的数量,要么产生新的采购订单。
至于负天数的情况,跟正天数大同小异,只不过产生的行动是预付(英文为Advanced,我觉得翻译成 提前 是不是会更容易理解一些?),这里就不再介绍了。
结论
我感觉AX里的重排假设还是符合APICS理论的,当然这只是很简单的测试。
先看一下APICS字典关于重排假设的定义:
rescheduling assumption--A fundamental assumption of MRP logic that existing open orders can be rescheduled in nearer time periods far more easily than new orders can be released and received.As a result,planned order receipts are not crteated until all scheduled receipts have been applied to cover gross requirements.
翻译一下大体意思是:
重排假设--MRP逻辑的基本假设,它认为重新排产短时期内的未结订单(指的是已经开工的或者订购的但还没有入库的生产订单或者采购订单)比从重新下达和接收新的计划订单容易得多。如果按照这个逻辑的话,在所有的预计接收量全部覆盖毛需求之前将不会产生新的计划订单。
Apics字典中的解释言简意赅,很多问题没有展开讲,关于这个问题<<MRPII Standard System>>这本书有很详细的论述。第6章<<The Netting and Exception Checking Logic of MRPII>>,下面大体说一下它讲述的意思,如果有理解不正确的地方,还望同行多多指教。
在创建和下达一个新的计划订单之前,净需求的逻辑假定已经存在的预计接收量将会被重排到一个更早的日期来满足需求。比如,下周存在一个未满足的需求,车间里有个生产订单还没完工,净需求的计算逻辑会假定这个订单会加速完成来满足需求。这种假设实际上是反映世界的真实情况,注意重排假设并不会假定这个生产订单一定会被加速并在下周完成,它只是假设如果有订单能在下周完工的话,应该是在车间加工的订单而不是新创建的订单,注意,净需求的计算逻辑并不会修改预计接收量的日期,它只是在做净需求计算时使用这个订单而已。在这本书的附录三里介绍了如果MRP不使用重排假设会产生的问题:
1.安排一个新的订单在已经存在的订单完工前完工,会让计划员或者采购员很难理解,一个已经在车间生产的订单显然会比一个新创建的订单更有可能先完成。向车间下达一个新的订单并要求它在已存在的订单前完工,没有意义。极端情况下,逻辑会变成不是根据要制造的产成品的数量,而是根据排产更改的次数去订购材料。
2.不考虑重排假设的会引起产品计划的不正确,并且只是问题的一部分,一旦一个新的订单被安排了,该产品的零部件的毛需求就会产生,由于这个新的订单的安排就是不正确的,那么它所产生的零部件的毛需求也不会正确,这样毛需求,计划订单和异常信息都会很快变得毫无意义,系统也就失败了,因为它已经不能用来模拟现实了。
上面的这些理论主要是介绍MRPII为什么要使用重排假设,那么系统应该怎么提醒计划员那?<<MRPII Standard System>>也给出了解决方法,向计划员提供重排异常信息。
当一个预计接收量的预计入库日期不足够早时,就会产生物料短缺,在这种情况下,就应该产生一个异常信息提示这个订单的完工日期应该提前以防止物料短缺的发生。
如果一个预计接受量的预计完工日期过早时,同样严重的问题也会产生,要么有用的能力用来生产错误的产品,或者正常的优先级逻辑将不能辨别什么是真正需要的和什么时候需要。所以在这种情况下,也应该产生一个异常信息,来提示需要将这个订单的完工入库日期向后排。
另外,有个争论就是为什么不让系统自己更改预计接收量的完工入库日期?这本书的作者的观点是,这是人的职责,计算机只负责提供异常信息,至于要不要调整是计划员的工作,计划员要为这件事情负责而不是计算机,即便是计算机帮计划员自动更改了日期,计划员还是有责任去重新看一遍看是否正确,与其这样还不如,让计划员自己去改。
AX中的实现
在进行之前,根据前面的描述,我们需要明确一个概念,在APICS字典中提到能修改的是in nearer time periods ,意思是更改相对近的期间内的预计收货量的的入库日期,但是在计算机实现的时候不能用nearer这样的人性化的模糊概念,必须要能量化,AX提供了两个参数来量化这个时间,也就是正天数和负天数,Positive Days和Negative Days.
主计划->设置->覆盖范围->覆盖范围组->常规选项卡

对照APICS理论部分的内容就很容易理解这个负天数和正天数的含义了,按照重排假设,如果预计收货量的入库日期比需求日期晚,那么系统需要给出一个将预计收货量的入库日期提前的提示信息,但是不能用无限期天数,比如让计划员修改几年后的一个生产订单的入库日期,那个开工日期还早着那,大可不必考虑。
负天数就是用来定义系统会考虑交货日期后多少天入库的预计收货量的入库日期。比如现在有一个需求日期为2009-09-18的销售订单,系统里已经有了2009-09-25和2009-10-28的两张还未入库的生产订单,如果负天数设置为10天,那么系统就只会考虑2009-09-25这张生产订单,给出提示修改它的完工入库日期和数量,而不会考虑2009-10-28的这张生产订单了,因为这张订单在需求日期的10天后。
同样正天数就比较好考虑了,正如上文提到的那样,<<MRPII Standard System>>也说了 如果一个预计接受量的预计完工日期过早时,也应该产生一个异常信息,来提示需要将这个订单的完工入库日期向后排。那么多久之前的预计收货量需要提示其延后那?就是这个正天数的作用了,这个天数不能设置的太小,要不然需求日期-正天数就会大于当前日期,那么就连当前的现有量都不会考虑了,这就不对了,一般设置不能小于该物料的提前期,因为一般情况下计划员至少要在提前期内开工要不然就不能按时完工了,所以完工日期-提前期应该是不大于当前日期的。
明白了正天数和负天数的概念,就比较容易看在AX里是怎么实现重排假设的了。
为了方便说明问题,简便期间,我们只创建一个简单的物料RA,其物料类型为物料。然后创建一个销售订单,让其产生毛需求,交货日期为2009-09-30,如下图所示:

这样物料RA就会有需求日期为2009-09-30的毛需求了,这时运行主计划,可以看到RA的计划采购订单。
这没有问题。
现在测试它的重排逻辑,先测试如果系统存在一个交货日期在2009-09-30之前预计接收量,假设收货日期为2009-09-20,我们让它在有效的范围内,那么正天数至少不能小于10天,我们设置正天数为20天,创建一个采购订单,设定交货日期为2009-09-20,数量恰好满足需求为200,如下图所示:

这时再运行Master Planning,理论上应该是不产生计划采购订单了,并且应该产生一条提示信息,让采购订单延后10天到2009-09-30交货。我们可以验证一下,运行Master Planning,查看计划订单不会看到有RA的计划采购订单生成了,再去看一下是否有让我们延迟交货的消息产生。
主计划->报表->覆盖范围->行动
选择我们刚刚运行的主计划,物料选择RA,如下图所示:

点击确定,查看结果

显然这个结果是符合预期的。
我们再来测试两种情况,如果已经存在的采购订单的数量大于需求,比如采购订单的数量是300,它应该怎么处理那?理论上,延期这个应该跟上面一样的,但是数量应该减少100个,修改采购订单数量为300,同样的步骤运行主计划,查看行动消息如下:

显然这个结果也是正确的。
最后一种情况,如果采购订单上的数量不足200个,比如是100个,应该怎么处理那?理论上应该,延期并且增加数量才对。修改采购订单数量为100,运行主计划,查看计划订单,我们会发现产生了一个数量为100的计划采购订单,如下图所示:
这条记录对应的消息如下:
AX给出的建议是取消这张计划订单,那么它对采购订单的建议采取什么动作那?运行报表查看结果如下:

无疑这个结果也是合情合理的,给了计划员两种选择,要么增加原来采购订单的数量,要么产生新的采购订单。
至于负天数的情况,跟正天数大同小异,只不过产生的行动是预付(英文为Advanced,我觉得翻译成 提前 是不是会更容易理解一些?),这里就不再介绍了。
结论
我感觉AX里的重排假设还是符合APICS理论的,当然这只是很简单的测试。