机器学习技法 之 终章（Final）

特征转换的技巧（Feature Exploitation Techniques）

核技巧（Kernel）

对于数值特征，使用一些映射函数 (Phi)，将想要的特征转换嵌入进 kernel 运算里面，在 kernel 运算里面就包含了特征转换和在转换后空间上取内积。（numerous features within some (Phi): embedded in kernel (K_Phi) with inner product operation）。

常用的核技巧有多项式核（Polynomial Kernel，缩放的多项式转换），高斯核（Gaussian Kernel，无限维的特征转换），树桩核（Stump kernel，将决策树桩作为转换函数）。当然对于这些核函数，可以使用求和（Sum）或求积（Product）进行组合，也可以提出新的满足 Mercer condition 的 Mercer kernel。

那么这些 kernel 便可以搭配上已有的 kernel 模型。比如 SVM，SVR，Probabilistic SVM，kernel ridge regression，kernel logistic regression。所以有了这里 kernel，便可以使用线性模型解决复杂的非线性问题。

聚合（Aggregation）

获取 (g_t (x)) 作为映射函数 (Phi) 预测特征，作为一种特征转换（predictive features within some (Phi) : (Phi_t (x) = g_t (x))）。

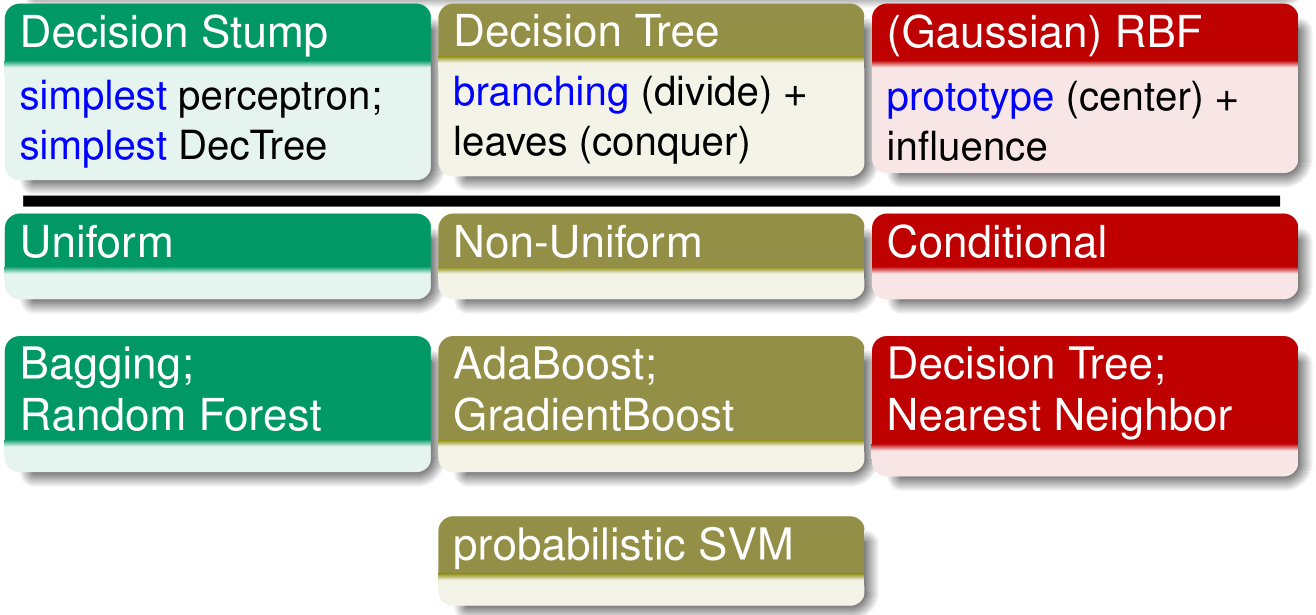
常用的 (g_t (x)) 有：决策树桩，决策树，RBF（找到一个中心，并学习出中心的影响力）。

有了这些 (g_t (x)) ，便可以使用一些 blending、bagging 或 boosting 方法了。其中 probabilistic SVM 则是将已有的 SVM 模型和 bias 进行融合的一个过程。

提取（Extraction）

对于隐含或潜藏的特征，使用一些映射函数 (Phi)，将这些特征提取出来。也就是说不认为已经给定了或者隐藏在某些 kernel 里面，而是需要进行最优化的一些变数。（hidden features within some (Phi) : as hidden variables to be ‘jointly’ optimized with usual weights — possibly with the help of unsupervised learning）

比如说神经网络或深度学习中神经元的权重，RBF 网络中 RBF 的中心，自适应提升和梯度提升中的 (g_t)，k-Means 算法中的聚类中心，自编码器和PCA获取的基底方向或投影放向。

压缩（Compression）

使用一些映射函数 (Phi) 将原始特征压缩到低维特征（low-dimensional features within some(Phi) : compressed from original features）

在决策树中，每一次的分支都是进入低维度空间进行操作。而随机森林中，每一次操作都会进行选择在一个随机的低维的特征空间进行操作。那在自编码器和PCA中则是找出低维的可以尽可能保留信息的特征表示。而矩阵分解也类似，是将只有零一的很高维特征映射到低维空间。

实际上，特征选择也是一种压缩方式，就是找出最有用的一些低维表示（‘most-helpful’ low-dimensional projection）。

最佳化的技巧（Error Optimization Techniques）

梯度下降法（Gradient Descent）

当误差函数的梯度的近似解被定义时，将其用于一阶估计：

[ ext { new variables } = ext { old variables } - eta abla E ]

即让变量沿着其梯度反方向变化，不断接近最优解。例如之前介绍过的SGD（沿着负梯度方向一小步一小步的寻优）、Steepest Descent（下降的速度最快，不再是一小步而是一大步） 和 Functional GD（下降方向是函数）都是利用了梯度下降的技巧。

当然如果有需求也可以使用有约束条件的梯度下降法，二阶估计等。

等效解决方案（Equivalent Solution）

当原问题很难求解时，对其等效问题求解。什么意思呢？对于一些更复杂的最优化问题，无法直接利用梯度下降方法来做，往往需要一些数学上的推导，对等效问题求解来得到最优解。

最典型的例子是 Dual SVM，还包括 Kernel LogReg 、Kernel RidgeReg 和 PCA 等等。这些模型本身包含了很多数学上的一些知识，例如线性代数等等。

除此之外，还有一些其他的 boosting 模型和 kernel 模型的现代求解器在很大程度上依赖于这种技术（运用到类似的数学推导和转换技巧）。

representer 指的是什么意思呢？求大佬指点

多步求解（Multiple Steps）

当原问题很难求解时，将其分为几个比较简单的子问题进行求解。这对于复杂模型来说很有效。

也就是将问题划分为多个步骤进行求解，即Multi­Stage。例如probabilistic SVM、linear blending、RBF Network等。还可以使用交叉迭代优化的方法，即 Alternating Optim。例如k­Means、alternating LeastSqr等。除此之外，还可以采样分而治之的方法，即Divide & Conquer。例如decision tree。

避免过拟合的技巧（Overfitting Elimination Techniques）

Feature Exploitation Techniques 和 Error Optimization Techniques都是为了优化复杂模型，减小 (E_{in}) 。但是 (E_{in}) 太小有很可能会造成过拟合overfitting。因此，机器学习中，Overfitting Elimination尤为重要。

正则化（Regularization）

如果模型太过强大，那一定要记得踩刹车，也就是正则化（Regularization），这可以说是最重要的技术。常用的方法包括：大间隔、L1/L2正则化、投票或平均、剪枝、降噪、加入限制条件等等。

验证（Validation）

除了Regularization之外，还可以使用Validation来消除Overfitting。Validation指的是当模型太过强大时，应当注意其性能和是否诚实（偷看测试资料）等。常用的 Validation 方法包括：交叉验证，支持向量的个数、OOB估计和内部验证（例如剪枝后验证模型的性能）等。虽然很简单，但是很有必要。

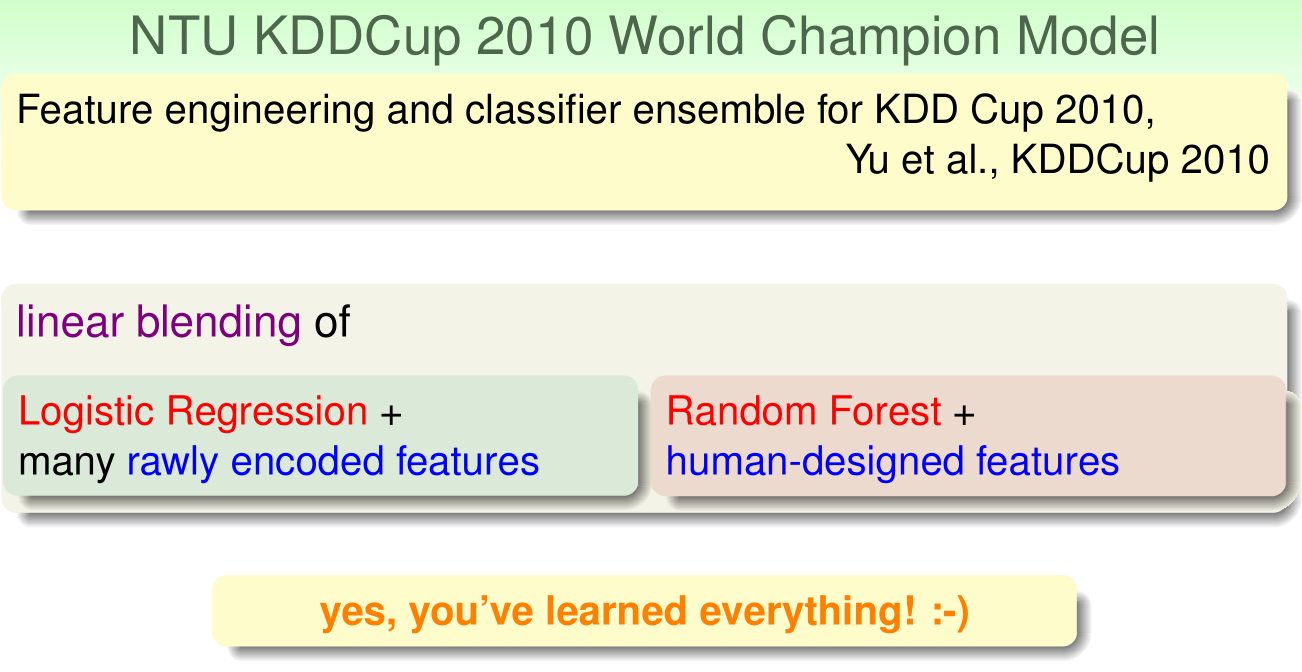
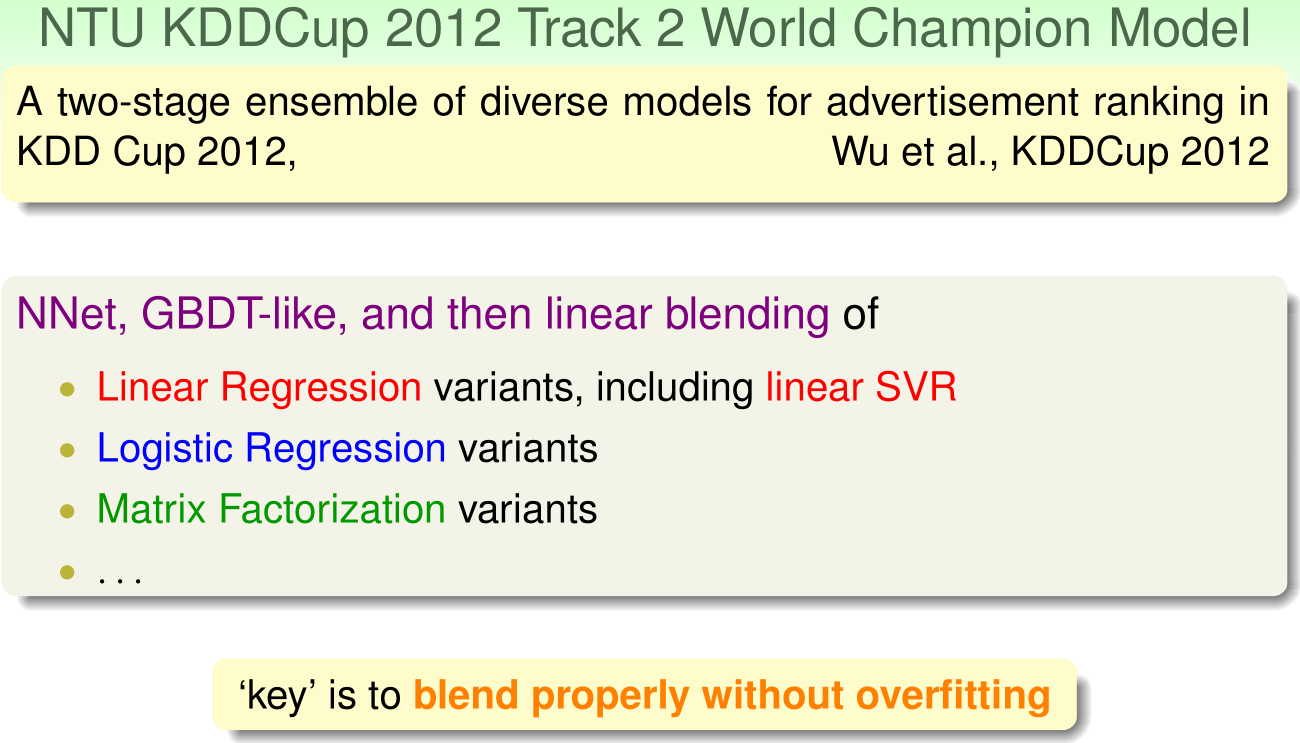
机器学习的实际运用（Machine Learning in Practice）

林轩田老师将其所在的台大团队在近几年的KDDCup国际竞赛上的表现和使
用的各种机器算法进行了介绍。相应的PPT图片如下：