数据结构 -- Trie字典树

简介

　　字典树：又称单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。

　　优点：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

　　性质：   1.  根节点不包含字符，除根节点外每一个节点都只包含一个字符；

　　　　　　2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串；

　　　　　　3.  每个节点的所有子节点包含的字符都不相同。

　　应用场景：用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。

　　　　　　

代码 实现

 本文使用链表来实现Trie字典树，字符串的每个字符作为一个Node节点，Node主要有两部分组成：

1. 是否是单词 (boolean isWord)
2. 节点所有的子节点，用map来保存 (Map next)

添加

public void add(String word) {
    Node current = root;
    char[] cs = word.toCharArray();
    for (char c : cs) {
        Node next = current.next.get(c);
        if (next == null) {
            //一个字符对应一个Node节点
            current.next.put(c, new Node());
        }
        current = current.next.get(c);
    }
    //current就是word的最后一个字符的Node
    
    //如果当前的node已经是一个word，则不需要添加
    if (!current.isWord) {
        size++;
        current.isWord = true;
    }
}

查找

　　Trie查找操作就比较简单了，遍历带查找的字符串的字符，如果每个节点都存在，并且待查找字符串的最后一个字符对应的Node的 isWord 属性为 true ，则表示该单词存在

public boolean contains(String word) {
    Node current = root;
    for (int i = 0; i < word.length(); i++) {
        char c = word.charAt(i);
        Node node = current.next.get(c);
        if (node == null) {
            return false;
        }
        current = node;
    }
    //current就是word的最后一个字符的Node
    return current.isWord;
}

前缀查询

public boolean containsPrefix(String prefix) {
    Node current = root;
    for (int i = 0; i < prefix.length(); i++) {
        char c = prefix.charAt(i);
        Node node = current.next.get(c);
        if (node == null) {
            return false;
        }
        current = node;
    }
    return true;
}

删除

Trie的删除操作就稍微复杂一些，主要分为以下3种情况：

　　1. 如果单词是另一个单词的前缀

　　　　如果待删除的单词是另一个单词的前缀，只需要把该单词的最后一个节点的 isWord 的改成false，比如Trie中存在 panda 和 pan 这两个单词，删除 pan ，只需要把字符 n 对应的节点的 isWord 改成 false 即可。

　　　　　　

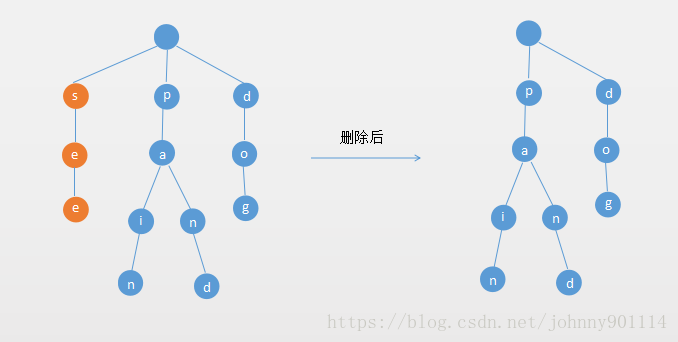
　　2. 如果单词的所有字母的都无分支，删除整个单词。

　　　　如果单词的所有字母的都没有多个分支（也就是说该单词所有的字符对应的Node都只有一个子节点），则删除整个单词。　　　　　　

　　　　　　

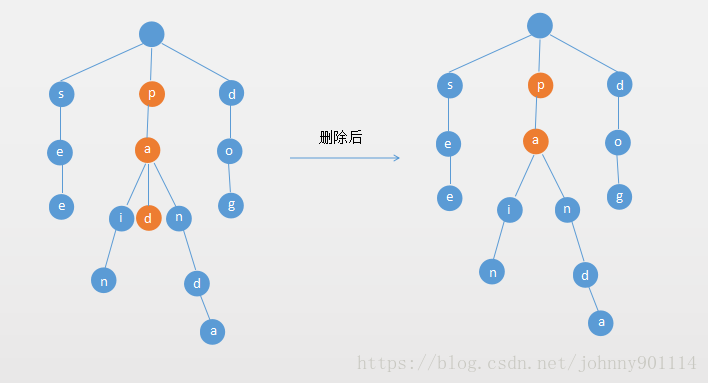
　　3. 如果单词的除了最后一个字母，其他的字母有多个分支

　　　　

 public boolean remove(String word){
        Node multiChildNode = null;
        int multiChildNodeIndex = -1;
        Node current = root;
        for (int i = 0; i < word.length(); i++) {
            Node child = current.next.get(word.charAt(i));
            //如果Trie中没有这个单词
            if (child == null) {
                return false;
            }
            //当前节点的子节点大于1个
            if (child.next.size() > 1) {
                multiChildNodeIndex = i;
                multiChildNode = child;
            }
            current = child;
        }
        //如果单词后面还有子节点
        if (current.next.size() > 0) {
            if (current.isWord) {
                current.isWord = false;
                size--;
                return true;
            }
            //不存在该单词，该单词只是前缀
            return false;
        }
        //如果单词的所有字母的都没有多个分支，删除整个单词
        if (multiChildNodeIndex == -1) {
            root.next.remove(word.charAt(0));
            size--;
            return true;
        }
        //如果单词的除了最后一个字母，其他的字母有分支
        if (multiChildNodeIndex != word.length() - 1) {
            multiChildNode.next.remove(word.charAt(multiChildNodeIndex + 1));
            size--;
            return true;
        }
        return false;
    }

Trie查询效率非常高，但是对空间的消耗还是挺大的，这也是典型的空间换时间。

可以使用 压缩字典树(Compressed Trie) ，但是维护相对来说复杂一些。

如果我们不止存储英文单词，还有其他特殊字符，那么维护子节点的集合可能会更多。

可以对Trie字典树做些限制，比如每个节点只能有3个子节点，左边的节点是小于父节点的，中间的节点是等于父节点的，右边的子节点是大于父节点的，这就是三分搜索Trie字典树(Ternary Search Trie)。

参考：https://blog.csdn.net/johnny901114/article/details/80711441