Codeforces Round #746 (Div. 2) 题解

旅行传送门

A. Gamer Hemose

题意：给你 \(n\) 种武器，每种武器可以造成 \(a_i\) 的伤害。现在你面对一名生命值为 \(H\) 的敌人，每次攻击你可以选择一种武器并对敌人造成相应伤害直至其死亡（ \(H \leq 0\) ）,但你不能连续两次都选择相同的武器。现问你最少需要攻击多少次可以解决掉敌人？

题目分析：贪心，由于不能连续两次使用相同的武器，所以轮换着使用伤害值最高的武器和伤害值次高的武器即可。

AC代码：

#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)

char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

int solve()
{
    int n, h;
    n = read(), h = read();
    std::vector<int> a(n + 1);
    rep(i, 1, n) a[i] = read();
    std::sort(a.begin() + 1, a.begin() + n + 1);
    int sum = a[n - 1] + a[n];
    int left = h % sum;
    int res = 2 * (h - left) / sum;
    while (left > 0)
    {
        left -= (res & 1) ? a[n - 1] : a[n];
        ++res;
    }
    return res;
}

int main(int argc, char const *argv[])
{
    int T = read();
    while (T--)
        printf("%d\n", solve());
    return 0;
}

B. Hemose Shopping

题意：给你一个长度为 \(n\) 的序列，你可以执行下列操作任意次：

• 交换两个下标分别为 \(i\) 与 \(j\) 的元素 \(a_i\) 与 \(a_j\) （ \(|i - j| \geq x\) ）

问是否可能通过有限次操作使得序列按非递减排序？

题目分析：运用集合的思想来考虑这个问题，对每个 \(i\) ，其与 \([i+x,n]\) 属于同一集合，我们可以将集合内的元素看成一个新序列，在这个新序列中交换元素不再有上述限制，因此必定能按非递减排序。不难发现，只有 \([n - x + 1, x]\) 内的元素不在集合中，因此合法的情况只有这些数最开始就待在它们本该待的地方，将它们与排序后的序列一一比对即可。

AC代码：

#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
const int maxn = 1e5 + 5;

char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

bool solve()
{
    int n = read(), x = read();
    std::vector<int> a(n + 1), b(n + 1);
    rep(i, 1, n) a[i] = b[i] = read();
    if (x <= n / 2)
        return true;
    std::stable_sort(b.begin() + 1, b.begin() + n + 1);
    rep(i, n - x + 1, x) if (a[i] ^ b[i]) return false;
    return true;
}

int main(int argc, char const *argv[])
{
    int T = read();
    while (T--)
        puts(solve() ? "YES" : "NO");
    return 0;
}

C. Bakry and Partitioning

题意：给你一棵含 \(n\) 个节点，每个节点权值为 \(a_i\) 的树，现问你能否将这棵树分为至少 \(2\) 个，至多 \(k\) 个连通块，且每个块的异或和都相等。

题目分析：首先求出整棵树的异或和 \(sum\) ，分类讨论：

• \(sum = 0\) ，说明只删一条边即可将整棵树分成两个异或和相等的连通块，显然可行
• \(sum \not= 0\) 且 \(k = 2\) ，假设此时 \(sum = x\) 且 \(x \not= 0\) ，若可将其分成两个异或和均为 \(y\) 的连通块，则有 \(y \bigoplus y = x = 0\) ，与假设矛盾，故不成立
• \(sum \not= 0\) 且 \(k > 2\) ，由于异或和的性质，相同的值异或奇数次不变，偶数次为 \(0\) 。因此我们通过 \(dfs\) 每找到一棵异或和为 \(sum\) 的子树，便将它单独拆出来，若最后能分成三个以上的连通块则可行。

用图解释就是：

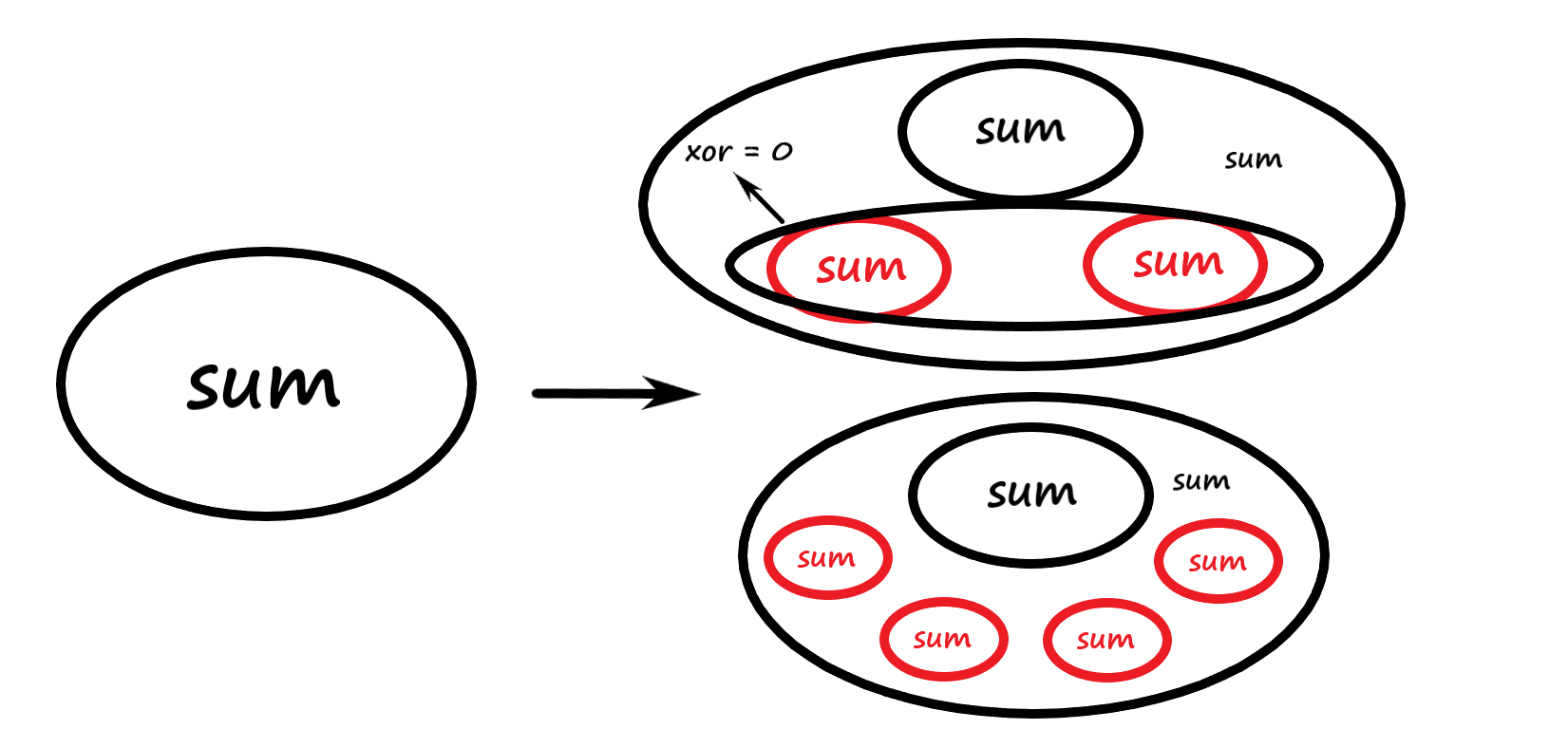
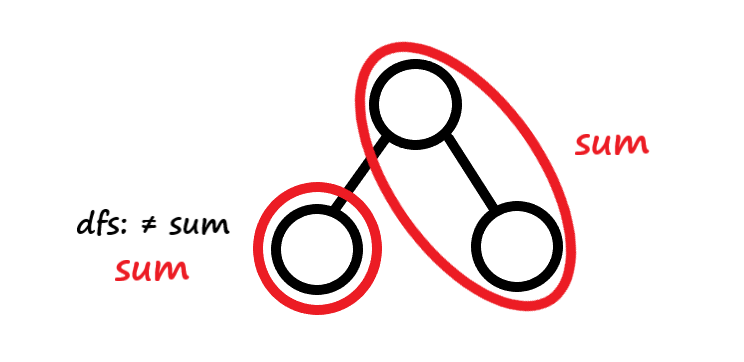
为什么拆出来的一定是子树呢？如图，因为 \(dfs\) 是自下而上搜索的，若拆出来的是一条链，说明这条链与那个单独拆出来的子节点的异或和均为 \(sum\) ，但 \(dfs\) 到这个子节点的时候并没有将它拆出来，说明它的异或和不为 \(sum\) ，与假设矛盾，故证。

AC代码：

#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
const int maxn = 1e5 + 5;

char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

int n, k, cnt, a[maxn], sum[maxn];
std::vector<int> g[maxn];

void init()
{
    cnt = 0;
    memset(sum, 0, sizeof(sum));
    rep(i, 1, n) g[i].clear();
}

void dfs(int u, int f)
{
    sum[u] ^= a[u];
    for (auto v : g[u])
    {
        if (v == f)
            continue;
        dfs(v, u);
        sum[u] ^= sum[v];
    }
    if (sum[u] == sum[0])
        ++cnt, sum[u] = 0;
}

bool solve()
{
    n = read(), k = read();
    init();
    rep(i, 1, n) a[i] = read();
    rep(i, 1, n - 1)
    {
        int u = read(), v = read();
        g[u].push_back(v);
        g[v].push_back(u);
    }
    rep(i, 1, n) sum[0] ^= a[i];
    if (!sum[0])
        return true;
    if (sum[0] && k < 3)
        return false;
    dfs(1, 0);
    return cnt >= 3 ? true : false;
}

int main(int argc, char const *argv[])
{
    int T = read();
    while (T--)
        puts(solve() ? "YES" : "NO");
    return 0;
}

E. Bored Bakry

题意：给你一个长度为 \(n\) 的序列 ，当一个子序列满足 \(a_l \& a_{l+1} \& a_{l+2}...\& a_r>a_l \bigoplus a_{l+1} \bigoplus a_{l+2}...\bigoplus a_r\) 时，我们称其为 \(good\) 子序列，现要你找出最长的 \(good\) 子序列。

题目分析：考虑什么情况下会满足一段区间的按位与 \(\& > \bigoplus\) ，根据按位与及异或和的性质，即存在二进制下某一位 \(i\) ，有：

• 对所有 \(> i\) 的位二者相等，即这段子序列在高位的按位与及前缀异或和为 \(0\)
• 在第 \(i\) 位上 \(\& > \bigoplus\) ，进一步可以推断出序列长为偶数，因为要让第 \(i\) 按位与占优，那第 \(i\) 位必定全为 \(1\) ，此时要让异或和较小，唯一的情况只有偶数个 \(1\) 异或
• 第 \(i\) 位上已有 \(\& > \bigoplus\) ，故 \(< i\) 的位不作考虑

接下来就是代码实现，我们从高位向低位枚举每一位二进制 \(i\) ，得到一个新的序列 \(b_i\) ，此时的 \(b_i\) 包含了高位与当前位的信息，然后从 \(b_i\) 中选出当前位为 \(1\) 的连续的一段去更新答案，更新时我们记录前缀异或和与每一个异或值首次出现的位置，这样就能同时保证选出的 \(good\) 序列长度为偶数且前缀异或和为 \(0\) ，原因如下：

• 根据异或和的性质： \(a_4 \bigoplus a_5 \bigoplus a_6 = (a_1 \bigoplus a_2 \bigoplus a_3) \bigoplus (a_1 \bigoplus a_2 \bigoplus...\bigoplus a_6)\) ，所以当前缀异或和有 \(sum_{l-1} = sum_{r}\) 时， \([l,r]\) 段的异或和为 \(0\)
• 因为我们同时存储了高位与当前位的信息，所以当 \(pos\) 数组发生更新的时候，即存在上述所言的 \(sum_{l-1} = sum_{r}\) 时，此时必定有高位前缀异或和为 \(0\) ，且当前位连续的一段 \(1\) 为偶数个

笔者水平有限（无论语文还是写题），有疑问或更好的做法请在评论区留言，不足之处请谅解，谢谢

AC代码：

#include <bits/stdc++.h>
#define rep(i, x, y) for (register int i = (x); i <= (y); i++)
#define down(i, x, y) for (register int i = (x); i >= (y); i--)
const int maxn = 1e6 + 5;

char buf[1 << 23], *p1 = buf, *p2 = buf, obuf[1 << 23], *O = obuf;
#define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
inline int read()
{
    int x = 0, f = 1;
    char ch = getchar();
    while (!isdigit(ch))
    {
        if (ch == '-')
            f = -1;
        ch = getchar();
    }
    while (isdigit(ch))
    {
        x = x * 10 + ch - '0';
        ch = getchar();
    }
    return x * f;
}

int n, ans, a[maxn], b[maxn], sum[maxn], pos[maxn];

int solve(int l, int r)
{
    if (l >= r)
        return 0;
    //记录前缀异或和
    sum[l - 1] = 0;
    rep(i, l, r) sum[i] = sum[i - 1] ^ b[i];
    //记录每一个异或值首次出现的位置
    //只有高位前缀异或和为 0 的情况下，sum才可能出现重复，pos才会发生更新
    down(i, r, l - 1) pos[sum[i]] = i;
    int res = 0;
    //异或和的性质，a4 ^ a5 ^ a6 = (a1 ^ a2 ^ a3) ^ (a1 ^ a2 ^...^ a6)
    //即 sum[l-1] = sum[r] ，则 [l,r] 的异或和为 0 ，保证了偶数段长度
    rep(i, l, r) res = std::max(res, i - pos[sum[i]]);
    return res;
}

int main(int argc, char const *argv[])
{
    n = read();
    rep(i, 1, n) a[i] = read();
    down(i, 20, 0)
    {
        //枚举每一位
        rep(j, 1, n) b[j] = a[j] >> i;
        int l = 1, r = 1;
        while (r <= n)
        {
            //将当前位为 1 的连续段选出来
            while (l <= n && !(b[l] & 1))
                ++l;
            r = l;
            while (r <= n && (b[r] & 1))
                ++r;
            ans = std::max(ans, solve(l, r - 1));
            l = r;
        }
    }
    printf("%d\n", ans);
    return 0;
}