Note sth about LDA(Linear Discriminant Analysis)
这篇来说说LDA的复习,LDA在第二次作业的博客中也提及了,但是那是作业思考,所以决定再开一篇只说LDA的。
动机:
LDA的中文名字——线性判别分析。其主要功能还是降维(N $
ightarrow$ k)。
LDA算法:(用一个二维特征的二分类来说明,因为图好画←_←)
至于多分类,可以参考博客LDA线性分析推广到多分类
明确LDA是如何进行降维(线性判别的),LDA考虑的和PCA不同之处在于——PCA的样本空间是一个样本,你来做主成分提取;而LDA的样本是一堆样本,你来找轴映射,从而将这些样本分离。于是乎,LDA考虑的目标是——最大化类间距离与最小化类内距离。(即不同类样本尽量离得远,同类尽量离得近)
算法公式概述:
$$ mu_i = frac{1}{N_i} sum_{x in X_i} x $$
$$ overline{z_i} = w^T mu_i = w^T frac{1}{N_i} sum_{x in X_i} x = frac {1}{N_i} sum_{x in X_i} w^Tx $$
Between-calss Scatter:$ J_b = || overline{z_1} - overline{z_2} || $
Within-class Scatter:$ J_w = s_1^2 + s_2^2 $,$ s_i = sum_{z in Z_i} (z-overline{z_i})^2 $
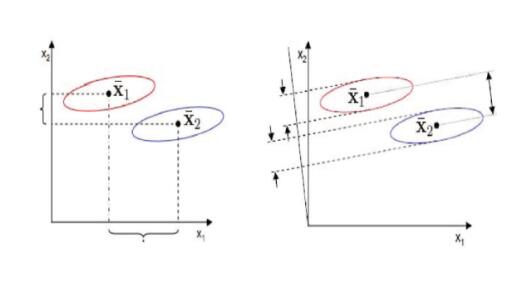
其实,上式中的$overline{z_i}$就是$i$这类的中心。即下图中的$overline{x_i}$,显然右图效果更好,因为左图其实两个类的部分样本映射完已经重叠了。
问题:
显然我们希望最大化$J_b$,而最小化$J_w$,而且是同时的,那么我们应该如何构造我们的优化目标函数?下面提供几个思路:
1、$ arg max J(w) = J_b - J_w $
2、$ arg max J(w) = frac{J_b}{J_w} = frac{w^T S_b w}{w^T S_w w} $
是不是都可以?当$J_b$变大而$J_w$减小的时候,让上述两个值最大,就是我们所需的答案。但是其实$J_b - J_w$是不可以的。因为还要考虑一个问题,虽然$J_b$和$J_w$都是正的,但是谁大谁小我们并不清楚,所以1式是会爆出负数的,而一旦爆出负数,结果就可能会出错,举个例子:$3-100>4-110$,但是$frac{3}{100}<frac{4}{110}$,显然就出错了。而2因为都是正数,所以可以很好地进行优化。
紧接着,我们观察一下$ arg max J(w) = frac{w^T S_b w}{w^T S_w w} $,会发现其实$w$的解是不唯一的,因为如果$w$是解,显然$a*w$也是解,为了方便得解出解,我们添加一个约束,并将问题转化为:$arg max J_b(w) = w^T S_b w$,其中$ w^T S_w w = 1 $,这个和$ arg max J(w) = frac{w^T S_b w}{w^T S_w w} $是等价的,但是我们可以发现——$arg max J_b(w) = w^T S_b w$,其中$ w^T S_w w = 1 $,又是一个带约束的优化问题,请出Lagrange-multipliers(拉格朗日乘子法)
我们可以得到:
$$ L(w,lambda) = w^T S_b w - lambda(w^T S_w w - 1) $$
$$ frac{partial L}{partial w} = 2S_b w - wS_w w $$
此时,若$S_w$可逆,则$S_{w}^{-1} S_b w = lambda w$,又回到了解特征方程的问题,如果$S_w$不可逆呢?我们可以求$S_w$的伪逆,这样问题也是可以解决的。
关于伪逆,即若$X$与$A^T$同型,且满足:$AXA=A$,$XAX=X$,则$X$为$A$的伪逆矩阵。