Android Matrix 方法详解

一、简介

Android android.graphics.Matrix 类是一个3 x 3的矩阵(方阵)，上一张几乎所有介绍Matrix的文章都会引用的Matrix内容图：

android.graphics.Matrix.png

Matrix使用非常广泛，平时我们使用的补间动画、图像变换、画布的变换、大名鼎鼎的MPAndroidChart图表库等都使用了Matrix。在平时的开发当中，Matrix的使用有时可以起到事半功倍的效果。

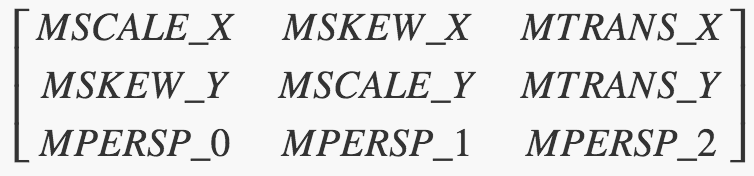
二、相关方法

1、equals

比较两个矩阵是否相等。

    Matrix matrix1 = new Matrix();
    Matrix matrix2 = new Matrix();
    matrix1.setTranslate(1,2);
    matrix2.setTranslate(2,2);
    // 输出：matrix1 == matrix2:false
    System.out.println("matrix1 == matrix2:" + matrix1.equals(matrix2));

2、+号相连/toString/toShortString

将矩阵转换为字符串。

    Matrix matrix = new Matrix();
    
    // 输出：+号相连：Matrix{[1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]}
    System.out.println("+号相连：" + matrix);
    // 输出：Matrix{[1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]}
    System.out.println("toString：" + matrix.toString());
    // 输出：[1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]
    System.out.println("toShortString：" + matrix.toShortString());

3、getValues()、setValues()

当我们调用Matrix类的getValues(float[] values)、setValues(float[] values)方法时，可以将这个矩阵转换成一个数组进行操作。转换后的数组为：
[ MSCALE_X, MSKEW_X, MTRANS_X, MSKEW_Y, MSCALE_Y, MTRANS_Y, MPERSP_0, MPERSP_1, MPERSP_2]
为了方便操作这个数组，在android.graphics.Matrix类中，定义了MSCALE_X、MSKEW_X...变量，分别代表各自功能在数组中对应的下标，具体内容如下：

public static final int MSCALE_X = 0;   //!< use with getValues/setValues
public static final int MSKEW_X  = 1;   //!< use with getValues/setValues
public static final int MTRANS_X = 2;   //!< use with getValues/setValues
public static final int MSKEW_Y  = 3;   //!< use with getValues/setValues
public static final int MSCALE_Y = 4;   //!< use with getValues/setValues
public static final int MTRANS_Y = 5;   //!< use with getValues/setValues
public static final int MPERSP_0 = 6;   //!< use with getValues/setValues
public static final int MPERSP_1 = 7;   //!< use with getValues/setValues
public static final int MPERSP_2 = 8;   //!< use with getValues/setValues

方法示例：

    Matrix matrix = new Matrix();
    
    // matrix = [1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]
    System.out.println("matrix = " + matrix.toShortString());

    float[] values = new float[9];
    matrix.getValues(values);
    
    // matrix转换成数组后 = [1.0, 0.0, 0.0, 0.0, 1.0, 0.0, 0.0, 0.0, 1.0]
    System.out.println("matrix转换成数组后 = " + Arrays.toString(values));

    // 为matrix赋值
    values [Matrix.MTRANS_X] = 2;
    values [Matrix.MTRANS_Y] = 3;
    matrix.setValues(values);

    // matrix = [1.0, 0.0, 2.0][0.0, 1.0, 3.0][0.0, 0.0, 1.0]
    System.out.println("matrix = " + matrix.toShortString());

4、setXXX/preXXX/postXXX

XXX可以是Translate、Scale、Rotate、Skew和Concat。其中Concat参数为Matrix，表示直接操作Matrix。由于缩放、旋转、错切可以绕中心操作，如果指定了中心，则变换步骤为：

1. 将原点平移到该点。
2. 做缩放、错切、旋转操作。
3. 原点平移到原来的原点处。

方法参数转换成了一个怎样的矩阵？

// 下面代码中参数(2,2) 转换后的矩阵为
// [2.0, 0.0, 0.0]
// [0.0, 2.0, 0.0]
// [0.0, 0.0, 1.0]
// 即根据XXX代表的功能修改矩阵中对应功能位置的值即可
matrix.postScale(2,2);

setXXX

首先会将该Matrix重置为单位矩阵，即相当于首先会调用reset()方法，然后再设置该Matrix中对应功能的值。例：

    // [1.0, 0.0, 0.0]
    // [0.0, 1.0, 0.0]
    // [0.0, 0.0, 1.0]
    Matrix matrix = new Matrix();

    // [1.0, 0.0, 0.0]    [2.0, 3.0, 4.0]
    // [0.0, 1.0, 0.0] -> [2.0, 0.0, 0.0]
    // [0.0, 0.0, 1.0]    [1.0, 1.0, 1.0]
    matrix.setValues(new float[]{2.0f,3.0f, 4.0f,
                                 2.0f,0.0f, 0.0f,
                                 1.0f,1.0f,1.0f});

    // [2.0, 3.0, 4.0]    [1.0, 0.0, 0.0]    [2.0, 0.0, 0.0]
    // [2.0, 2.0, 0.0] -> [0.0, 1.0, 0.0] -> [0.0, 2.0, 0.0]
    // [1.0, 1.0, 1.0]    [0.0, 0.0, 1.0]    [0.0, 0.0, 1.0]
    matrix.setScale(2,2);

preXXX

不会重置Matrix，相当于当前操作矩阵(A)左乘参数矩阵(B)，即AB。例：

    // [1.0, 0.0, 0.0]
    // [0.0, 1.0, 0.0]
    // [0.0, 0.0, 1.0]
    Matrix matrix = new Matrix();
    
    // [1.0, 0.0, 0.0]    [2.0, 3.0, 4.0]
    // [0.0, 1.0, 0.0] -> [2.0, 0.0, 0.0]
    // [0.0, 0.0, 1.0]    [1.0, 1.0, 1.0]
    matrix.setValues(new float[]{2.0f,3.0f, 4.0f,
                                 2.0f,0.0f, 0.0f,
                                 1.0f,1.0f,1.0f});
    
    // [2.0, 3.0, 4.0]           [2.0, 0.0, 0.0]   [4.0, 6.0, 4.0]
    // [2.0, 0.0, 0.0](matrix) * [0.0, 2.0, 0.0] = [4.0, 0.0, 0.0](matrix)
    // [1.0, 1.0, 1.0]           [0.0, 0.0, 1.0]   [2.0, 2.0, 1.0]
    matrix.preScale(2,2);

postXXX

不会重置Matrix，相当于当前操作矩阵(A)右乘参数矩阵(B)，即BA，例：

    // [1.0, 0.0, 0.0]
    // [0.0, 1.0, 0.0]
    // [0.0, 0.0, 1.0]
    Matrix matrix = new Matrix();
    
    // [1.0, 0.0, 0.0]    [2.0, 3.0, 4.0]
    // [0.0, 1.0, 0.0] -> [2.0, 0.0, 0.0]
    // [0.0, 0.0, 1.0]    [1.0, 1.0, 1.0]
    matrix.setValues(new float[]{2.0f,3.0f, 4.0f,
                                 2.0f,0.0f, 0.0f,
                                 1.0f,1.0f,1.0f});
    
    // [2.0, 0.0, 0.0]   [2.0, 3.0, 4.0]            [4.0, 6.0, 8.0]
    // [0.0, 2.0, 0.0] * [2.0, 0.0, 0.0] (matrix) = [4.0, 0.0, 0.0](matrix)
    // [0.0, 0.0, 1.0]   [1.0, 1.0, 1.0]            [1.0, 1.0, 1.0]
    matrix.postScale(2,2);

setContact

关于setContact(Matrix m1,Matrix m2)方法，需要单独说下，它的参数为两个Matrix对象，计算规则为：当前操作的Matrix对象 = m1 * m2;
例：

    // [1.0, 0.0, 0.0]
    // [0.0, 1.0, 0.0]
    // [0.0, 0.0, 1.0]
    Matrix matrix = new Matrix();
    Matrix matrix1 = new Matrix();
    Matrix matrix2 = new Matrix();

    // [1.0, 0.0, 0.0]    [2.0, 3.0, 4.0]
    // [0.0, 1.0, 0.0] -> [2.0, 0.0, 0.0]
    // [0.0, 0.0, 1.0]    [1.0, 1.0, 1.0]
    matrix1.setValues(new float[]{2.0f,3.0f, 4.0f,
                                 2.0f,0.0f, 0.0f,
                                 1.0f,1.0f,1.0f});

    // [1.0, 0.0, 0.0]    [2.0, 5.0, 4.0]
    // [0.0, 1.0, 0.0] -> [3.0, 0.0, 0.0]
    // [0.0, 0.0, 1.0]    [1.0, 2.0, 1.0]
    matrix2.setValues(new float[]{2.0f,5.0f, 4.0f,
                                 3.0f,0.0f, 0.0f,
                                 1.0f,2.0f,1.0f});

    // [2.0, 3.0, 4.0]            [2.0, 5.0, 4.0]            [17.0, 18.0, 12.0]
    // [2.0, 2.0, 0.0](matrix1) * [3.0, 0.0, 0.0](matrix2) = [4.0,  10.0, 8.0 ] (matrix)
    // [1.0, 1.0, 1.0]            [1.0, 2.0, 1.0]            [6.0,  7.0,  5.0 ]
    matrix.setConcat(matrix1,matrix2);

5、mapRadius/mapPoints/mapRect/mapVectors

可翻译为将矩阵映射到（作用于）点、矩形、半径、向量。

mapRadius

半径的计算。例：

    // 一个半径为100.0f的圆，放大1倍后，半径也将增大一倍。据说用在画布中的圆随画布大小变化时
    float radius = 100.0f;
    float radiusAfterMatrix;
    Matrix matrixRadius = new Matrix();
    matrixRadius.setScale(2,2);
    radiusAfterMatrix = matrixRadius.mapRadius(radius);
    // 输出：radius=200.0
    System.out.println("radius=" + radiusAfterMatrix);

mapPoints

此方法有3个重载方法。点数组各值分别代表pts[x0,y0,x1,y1 ... xn,yn],因为一个点的确定需要x坐标和y坐标两个值，所以，pts数组的长度一般为偶数，如果为奇数，则最后一个值不参与计算（长度为1将不计算）。下面给出具体例子，例子中将会详细说明mapPoints方法。

    // =======================
    // mapPoints(float[] pts)
    // =======================
    // 运算后的结果会保存在pts数组中，原pts数组中的内容会被覆盖

    // 1.《点的移动》,对于任意点(Xn,Yn),x轴方向平移dx,y轴方向平移dy后有：
    //  Xn = Xn + dx
    //  Yn = Yn + dy
    float[] ptsTrans = {6,2};
    Matrix matrixTrans = new Matrix();
    matrixTrans.setTranslate(-2,2);
    matrixTrans.mapPoints(ptsTrans);
    // 输出：trans=[4.0, 4.0]
    System.out.println("trans=" + Arrays.toString(ptsTrans));

    // 2.《点的放大》，对于任意点(Xn,Yn),绕点(px,py)x轴、y轴方向分别放大sx倍、sy倍后，有：
    //  Xn = Xn * sx + (px - px * sx)
    //  Yn = Yn * sy + (py - sy * py)
    float[] ptsScale = {2,3};
    Matrix matrixScale = new Matrix();
    matrixScale.setScale(3,6,2,2);
    matrixScale.mapPoints(ptsScale);
    // 输出：scale=[2.0, 8.0]
    System.out.println("scale=" + Arrays.toString(ptsScale));

    // 3.《点的旋转》，对于任意点(Xn,Yn),绕点(px,py)旋转a度后，有：
    //  Xn = (Xn - px) * cos(a) - (Yn - py) * sin(a) + px
    //  Yn = (Xn - px) * sin(a) + (Yn - py) * cos(a) + py
    float[] ptsRotate = {6,6};
    Matrix matrixRotate = new Matrix();
    matrixRotate.preRotate(90,2,3);
    matrixRotate.mapPoints(ptsRotate);
    // 输出：rotate=[-1.0,7.0]
    System.out.println("rotate=" + Arrays.toString(ptsRotate));

    // 4.《点的错切》,对于任意点(Xn,Yn),绕点(px,py)x轴、y轴方向分别错切kx、ky后，有：
    //  Xn = Xn + kx(Yn - py)
    //  Yn = Yn + ky(Xn - px)
    float[] ptsSkew = {3,2};
    Matrix matrixSkew = new Matrix();
    matrixSkew.setSkew(2,3,6,8);
    matrixSkew.mapPoints(ptsSkew);
    // 输出：skew=[-9.0,-7.0]
    System.out.println("skew=" + Arrays.toString(ptsSkew));

    // ===================================
    // mapPoints(float[] dst, float[] src)
    // ===================================
    // 运算后的结果保存在dst数组中，原src数组中的内容会保留

    float[] src = {2,3,3,3};
    float[] dst = new float[src.length];
    Matrix matrixDstSrc = new Matrix();
    matrixDstSrc.setTranslate(2,3);
    matrixDstSrc.mapPoints(dst,src);

    // 输出：dst=[4.0,6.0,5.0,6.0]
    System.out.println("dst=" + Arrays.toString(dst));
    // 输出：src=[2.0,3.0,3.0,3.0]
    System.out.println("src=" + Arrays.toString(src));

    // ==============================================================================
    // mapPoints(float[] dst,   ---- 计算结果存放数组
    //           int dstIndex,  ---- dst数组存放计算结果时起始下标
    //           float[] src,   ---- 计算的源数组
    //           int srcIndex,  ---- 源数组计算时起始下标
    //           int pointCount ---- 从起始下标开始一共要计算多少个点
    //           )
    // ==============================================================================
    // 运算后的结果保存在dst数组中

    float[] src1 = {2,3,3,3,2,3};
    float[] dst1 = new float[]{6,6,6,6,6,6};
    Matrix matrixDstSrc1 = new Matrix();
    matrixDstSrc1.setTranslate(1,1);

    // 1）从src1下标为2的位置开始计算，计算1个点，注意，是一个点，不是一个长度；计算的结果只保存计算的点，未计算的点将舍弃，即结果为：[4.0,4.0]
    // 2）将src1计算后的结果，从dst1下标为2的位置开始放置
    // 注意，从存放数组开始的位置存放计算结果时，如果长度不够，将抛出 ArrayIndexOutOfBoundsException 异常
    matrixDstSrc1.mapPoints(dst1,5,src1,2,1);

    // 输出：dst=[0.0,0.0,2.0,3.0,4.0,4.0]
    System.out.println("dst1=" + Arrays.toString(dst1));
    // 输出：src=[2.0,3.0,3.0,3.0,2.0,3.0]
    System.out.println("src1=" + Arrays.toString(src1));

mapRect

将矩形的4个点按Matrix中设定的值变换，返回值为变换后是否还为一个矩形。此方法有2个重载方法。

    // ============================================
    // mapRect(RectF rect)
    // ============================================
    // 结果存放在rect中，原rect将被覆盖
    RectF rectF = new RectF(100,100,200,200);
    // 输出：rectFbefore = RectF(100.0, 100.0, 200.0, 200.0)
    System.out.println("rectFbefore = " + rectF);
    Matrix matrixRectF = new Matrix();
    matrixRectF.setScale(2,2);
    matrixRectF.mapRect(rectF);
    // 输出：rectFafter = RectF(200.0, 200.0, 400.0, 400.0)
    System.out.println("rectFafter = " + rectF);

    // ============================================
    // mapRect(RectF dst,RectF src)
    // ============================================
    // 结果存放在dst中，原src会保留。其它与mapRect(RectF rect)方法相同

mapVectors

用法和mapPoints方法类似，此方法有3个重载方法，唯一不同的是mapVectors不受位移影响。例：

    float[] vector = {2,3};
    float[] point = {2,3};
    Matrix matrixTranslate = new Matrix();
    matrixTranslate.setTranslate(2,3);
    matrixTranslate.mapVectors(vector);
    matrixTranslate.mapPoints(point);

    // 输出：vector = [2.0,3.0]
    System.out.println("vector = " + Arrays.toString(vector));
    // 输出：point = [4.0,6.0]
    System.out.println("point = " + Arrays.toString(point));

6、invert

做相反的运算。得到变化前的状态。例：图形旋转一定角度后再恢复旋转前的状态。matrixOri.invert(matrixInvert)方法可翻译为：将matrixOri这个矩阵反转后存放在matrixInvert这个矩阵中， matrixInvert这个矩阵中原来的值将被覆盖。

    // ==========================================
    // 移动
    // ==========================================
    // [1.0, 0.0, Δx]            [1.0, 0.0, -Δx]
    // [0.0, 1.0, Δy]  invert -> [0.0, 1.0, -Δy]
    // [0.0, 0.0, 1.0]           [0.0, 0.0, 1.0]

    Matrix matrixTrans = new Matrix();
    matrixTrans.setTranslate(2,3);

    // [1.0, 0.0, 2.0]
    // [0.0, 1.0, 3.0]
    // [0.0, 0.0, 1.0]
    System.out.println("matrixTrans = " + matrixTrans);

    matrixTrans.invert(matrixTrans);

    // [1.0, 0.0, -2.0]
    // [0.0, 1.0, -3.0]
    // [0.0, 0.0,  1.0]
    System.out.println("matrixTrans = " + matrixTrans);

    // ==========================================
    // 缩放
    // ==========================================
    // [sx,   0,  -px]             [1/sx,    0,  px/2]
    // [0,   sy,  -py]  invert ->  [0,    1/sy,  py/2]
    // [0.0, 0.0, 1.0]             [0.0,   0.0,   1.0]

    Matrix matrixScale = new Matrix();
    matrixScale.setScale(2,2,12,7);

    // [2.0, 0.0, -12.0]
    // [0.0, 2.0, -7.0]
    // [0.0, 0.0, 1.0]
    System.out.println("matrixScale = " + matrixScale);

    matrixScale.invert(matrixScale);

    // [0.5, 0.0, 6.0]
    // [0.0, 0.5, 3.5]
    // [0.0, 0.0, 1.0]
    System.out.println("matrixScale = " + matrixScale);

7、isIdentity

判断一个矩阵是否为单位矩阵

    Matrix matrix = new Matrix();

    // 输出：matrix is identity:true
    System.out.println("matrix is identity:" + matrix.isIdentity());

    matrix.setTranslate(1,2);

    // 输出：matrix is identity:false
    System.out.println("matrix is identity:" + matrix.isIdentity());

8、setPolyToPoly

根据src坐标到dst坐标的变换关系，生成对应的Matrix矩阵。

    // ==================================================================================================
    // setPolyToPoly(float[] src,     变换前的点数组，内容为[x0, y0, x1, y1, ...]
    //               int srcIndex,    第一个变化的点在src数组中的下标
    //               float[] dst,     src变换后的点数组，内容为[x0‘, y0’, x1’, y1’, ...]，与src数组一一对应
    //               int dstIndex,    变化后的第一个点在dst数组中存储的位置
    //               int pointCount   一次一共需要变换多少个点，取值范围[0,4]
    //               )
    // ==================================================================================================

    float[] src = {1,2};
    float[] dst = {2,4};

    //          [1.0, 0.0, 0.0]
    // matrix = [0.0, 1.0, 0.0]
    //          [0.0, 0.0, 1.0]
    Matrix matrix = new Matrix();
    System.out.println("matrix = " + matrix.toShortString());

    matrix.setPolyToPoly(src,0,dst,0,1);

    //          [1.0, 0.0, 1.0]
    // matrix = [0.0, 1.0, 2.0]
    //          [0.0, 0.0, 1.0]
    System.out.println("matrix = " + matrix.toShortString());

    // 验证这个生成的matrix是否正确
    // [1.0, 0.0, 1.0]   [1]   [2.0]
    // [0.0, 1.0, 2.0] * [2] = [4.0]
    // [0.0, 0.0, 1.0]   [1]   [1.0]

9、setRectToRect

将矩形填充到矩形中。其中在填充时可以指定4种填充模式，这4种模式用Matrix.ScaleToFit枚举类型表示，关于这4种填充模式，借用一张官方demo图：

ScaleToFit.png

    Matrix matrix = new Matrix();
    RectF rectFSrc = new RectF(100,100,200,400);
    RectF rectFDst = new RectF(100,100,400,200);
    matrix.setRectToRect(rectFSrc,rectFDst, Matrix.ScaleToFit.FILL);

三、总结

Matrix可以运用到很多地方，但基本的原理都是通过Matrix提供的API对Matrix中值的更改，然后再将这个Matrix作用于不同的对象（图片、画布等）。

本篇文章主要是对android.graphics.Matrix类中常用方法的讲解，与网上其它讲解Matrix的文章方向可能有所不同。由于文章很多细致的讲解都在代码的注释中，请各位一定要关注文章中的代码示例。文章中的代码示例均可复制>>粘贴>>运行，可自行测试。

由于本人功力有限，文章中可能会有出错的地方。如果各位发现有误的地方请指证。当然，如果有什么地方不理解，也可以提出来。