Description [HAOI2010]软件安装
(n)个软件,每个软件有两个属性(w,v)表示占用空间和安装它的价值,但对于每一个软件都有一个依赖软件,只有安装了依赖软件并且依赖软件能正常工作,这个软件才能正常工作,不正常工作的软件占用空间并且不算价值。由于磁盘空间有限,现在问你在有限的(W)空间中,能得到的最大价值是多少。
Solution
一眼看去,背包特点。注意到有两个属性,并且还带有依赖,树形DP就ok,再加上一个(tarjan)缩点就完事儿。
普通树形DP(code) :原博客,侵删致歉
void dfs(int u) {
for(int i=cost[u];i<=m;i++)f[u][i]=val[u];
for(int i=hag[u];i!=-1;i=dag[i].next) {
int v=dag[i].to;
dfs(v);
for(int j=m-cost[u];j>=0;j--)
for(int q=0;q<=j;q++)
f[u][j+cost[u]]=max(f[u][j+cost[u]],f[u][j+cost[u]-q]+f[v][q]);
}
}
int main() {
.....
cost[s]=0;val[s]=0;
dfs(s);
printf("%d",f[s][m+cost[s]]);
return 0;
}
但我就不,用
泛化物品优化树形DP
-
什么是泛化物品:
泛化物品是一个价值和体积都不确定的物品,它的价值随着你给它分配的体积改变。
-
为什么要用泛化物品优化:
普通的树形DP一般来说时间复杂度是(O(nk^2))的,而用泛化物品优化可以达到(O(nk))的复杂度。
假设(f[u][i])为从(u)到根节点路径上,所有旁路中选体积(i)的最大价值。具体是这样:
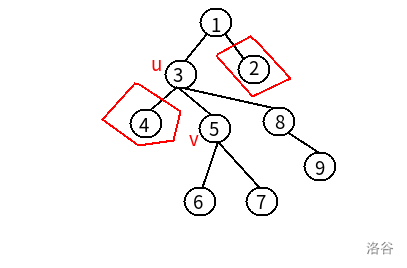
(图上的序号是DFS序) 从根节点到(v)的路径上的旁路就是圈起来的部分。所以一个点的旁路一定要是在它之前被遍历过的,即8号点不是(v)的旁路。
那么对于状态转移方程,则要如下设计:((v)是(u)的儿子节点)
[egin{cases}
f[v][i]=max(f[u][i]+val[v])(遍历v前)\
f[u][i]=max(f[u][i],f[v][i-wei[v]])(遍历v后)\
end{cases}
]
大概主要的思想就是在更新(u)时,当搜索(v)之后,为(u)的其他儿子预留空间。所以说每一次的(dp)更新都是有上限的。
综上,我们可以得到以下DP:
inline void dfs (int u,int mx) {
for (int i=0;i<g[u].size();i++) {
int v=g[u][i];
for (int j=mx-W[v];j>=0;j--) f[v][j]=max(f[v][j],f[u][j]+V[v]);
dfs(v,mx-W[v]);
for (int j=mx;j>=W[v];j--) f[u][j]=max(f[u][j],f[v][j-W[v]]);
}
}
这样再加个(tarjan)就可以啦
Code
#include<iostream>
#include<cstdio>
#include<vector>
#define pb push_back
using namespace std;
const int N=105,M=505;
int n,m,w[N],v[N],W[N],V[N],f[N][M],vis[N][N],du[N],rt;
int dfs_time,st[N],low[N],dfn[N],col,be[N],top;
vector<int> e[N],g[N],co[N];
inline int read () {
int res=0,fl=1;
char ch;
while ((ch=getchar())&&(ch<'0'||ch>'9')) if (ch=='-') fl=-1;
res=ch^48;
while ((ch=getchar())&&ch>='0'&&ch<='9') res=(res<<1)+(res<<3)+(ch^48);
return res*fl;
}
inline void tarjan (int u) {
low[u]=dfn[u]=++dfs_time;
st[++top]=u;
for (int i=0;i<e[u].size();i++) {
int v=e[u][i];
if (dfn[v]==-1) {
tarjan(v);
low[u]=min(low[u],low[v]);
} else if (!be[v]) low[u]=min(low[u],dfn[v]);
}
if (low[u]==dfn[u]) {
co[++col].pb(u);
be[u]=col;
if (u==0) rt=col;
while (st[top]!=u) {
co[col].pb(st[top]);
be[st[top]]=col;
if (st[top]==0) rt=col;
top--;
}
top--;
}
}
inline void dfs (int u,int mx) {
for (int i=0;i<g[u].size();i++) {
int v=g[u][i];
for (int j=mx-W[v];j>=0;j--) f[v][j]=max(f[v][j],f[u][j]+V[v]);
dfs(v,mx-W[v]);
for (int j=mx;j>=W[v];j--) f[u][j]=max(f[u][j],f[v][j-W[v]]);
}
}
int main () {
#ifndef ONLINE_JUDGE
freopen("software.in","r",stdin);
freopen("software.out","w",stdout);
#endif
n=read();m=read();
for (int i=1;i<=n;i++) w[i]=read(),low[i]=dfn[i]=-1;
for (int i=1;i<=n;i++) v[i]=read();
for (int i=1;i<=n;i++) {
int x=read();
e[x].pb(i);
}
for (int i=0;i<=n;i++) if (dfn[i]==-1) tarjan(i);
for (int i=0;i<=n;i++)
for (int j=0;j<e[i].size();j++) {
int to=e[i][j];
if (be[i]==be[to]||vis[be[i]][be[to]]) continue;
du[be[to]]++;
vis[be[i]][be[to]]=1;
g[be[i]].pb(be[to]);
}
for (int i=1;i<=col;i++) if (du[i]==0&&i!=rt) g[be[0]].pb(i);
for (int i=1;i<=n;i++) W[be[i]]+=w[i],V[be[i]]+=v[i];
dfs(be[0],m);
int ans=0;
for (int i=0;i<=m;i++) ans=max(ans,f[be[0]][i]);
printf("%d
",ans);
return 0;
}